本文主要是介绍算法leetcode|85. 最大矩形(rust重拳出击),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 85. 最大矩形:
- 样例 1:
- 样例 2:
- 样例 3:
- 样例 4:
- 样例 5:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
85. 最大矩形:
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
样例 1:
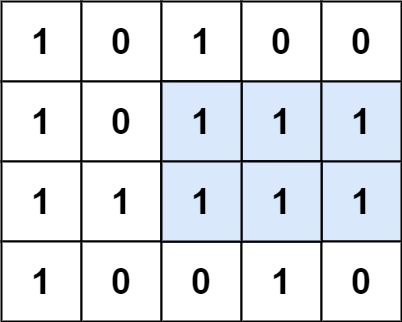
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]输出:6解释:最大矩形如上图所示。
样例 2:
输入:matrix = []输出:0
样例 3:
输入:matrix = [["0"]]输出:0
样例 4:
输入:matrix = [["1"]]输出:1
样例 5:
输入:matrix = [["0","0"]]输出:0
提示:
- rows == matrix.length
- cols == matrix[0].length
- 1 <= row, cols <= 200
- matrix[i][j] 为 ‘0’ 或 ‘1’
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 要不是刚做过 84. 柱状图中最大的矩形 这道题,差点就被唬住,就去暴力破解了。
- 可以从上到下的遍历,把矩阵按照柱状图处理,纵向从下往上计算高度,遇到0停止。
- 处理柱状图最直接的想法是双循环,遍历每个柱子,查找左边第一个低于自己的柱子,和右边第一个低于自己的柱子,这样就能算出当前柱子这个高度最大的宽度,有搞头,很明显会很慢,还有没有更好的办法呢。
- 找到每个柱子的左右边界(第一个低于自己的柱子)是关键,有没有办法降低查找的复杂度呢?
- 要是能一次遍历就把左右边界找到就好了,祭出神器单调栈,如果栈为空就入栈(这里可以使用技巧,让处理逻辑统一),否则判断下一个柱子如果高于栈顶或者和栈顶一样高也直接入栈,如果低于栈顶就出栈,因为当前这个柱子就是栈顶元素的右边界,重复这个过程,就可以在一次遍历的过程中就找到左右边界。
- 特别要注意遍历过程中栈为空,和遍历完所有柱子但是栈不为空的情况。
题解:
rust:
impl Solution {pub fn maximal_rectangle(matrix: Vec<Vec<char>>) -> i32 {let mut ans = 0;let (rows, cols) = (matrix.len(), matrix[0].len());let mut heights = vec![0; cols];let mut stack = vec![-1];(0..rows).for_each(|i| {(0..cols).for_each(|j| {// 矩阵转换为柱状图(滚动数组)if matrix[i][j] == '1' {heights[j] += 1;} else {heights[j] = 0;}while stack.len() > 1 && heights[*stack.last().unwrap() as usize] > heights[j] {// 栈中比当前位置高的那些待确定右边界的下标都可以确定右边界了ans = ans.max(heights[stack.pop().unwrap() as usize] * (j as i32 - 1 - stack.last().unwrap()));}// 入栈,等到能够确定右边界时处理stack.push(j as i32);});while stack.len() > 1 {// 栈中剩余的都是右边没有更低的ans = ans.max(heights[stack.pop().unwrap() as usize] * (cols as i32 - 1 - stack.last().unwrap()));}});return ans;}
}
go:
func maximalRectangle(matrix [][]byte) int {max := func(x, y int) int {if x > y {return x}return y}ans := 0rows, cols := len(matrix), len(matrix[0])heights := make([]int, cols)stack := []int{-1}for i := 0; i < rows; i++ {for j := 0; j < cols; j++ {// 矩阵转换为柱状图(滚动数组)if matrix[i][j] == '1' {heights[j]++} else {heights[j] = 0}for len(stack) > 1 && heights[stack[len(stack)-1]] > heights[j] {// 栈中比当前位置高的那些待确定右边界的下标都可以确定右边界了ans = max(ans, heights[stack[len(stack)-1]]*(j-1-stack[len(stack)-2]))// 出栈stack = stack[:len(stack)-1]}// 入栈,等到能够确定右边界时处理stack = append(stack, j)}for len(stack) > 1 {// 栈中剩余的都是右边没有更低的ans = max(ans, heights[stack[len(stack)-1]]*(cols-1-stack[len(stack)-2]))// 出栈stack = stack[:len(stack)-1]}}return ans
}
c++:
class Solution {
public:int maximalRectangle(vector<vector<char>>& matrix) {int ans = 0;const int rows = matrix.size();const int cols = matrix[0].size();int heights[cols];memset(heights, 0, sizeof(int) * cols);stack<int> s;s.push(-1);for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {// 矩阵转换为柱状图(滚动数组)if (matrix[i][j] == '1') {heights[j] += 1;} else {heights[j] = 0;}while (s.size() > 1 && heights[s.top()] > heights[j]) {// 栈中比当前位置高的那些待确定右边界的下标都可以确定右边界了int height = heights[s.top()];s.pop();ans = max(ans, height * (j - 1 - s.top()));}// 入栈,等到能够确定右边界时处理s.push(j);}while (s.size() > 1) {// 栈中剩余的都是右边没有更低的int height = heights[s.top()];s.pop();ans = max(ans, height * (cols - 1 - s.top()));}}return ans;}
};
python:
class Solution:def maximalRectangle(self, matrix: List[List[str]]) -> int:ans = 0rows = len(matrix)cols = len(matrix[0])heights = [0] * colsstack = [-1]for i in range(rows):for j in range(cols):# 矩阵转换为柱状图(滚动数组)if matrix[i][j] == '1':heights[j] += 1else:heights[j] = 0while len(stack) > 1 and heights[stack[-1]] > heights[j]:# 比当前位置高的那些待确定右边界的下标都可以确定右边界了ans = max(ans, heights[stack.pop()] * (j - 1 - stack[-1]))# 入栈,等到能够确定右边界时处理stack.append(j)while len(stack) > 1:# 栈中剩余的都是右边没有更低的ans = max(ans, heights[stack.pop()] * (cols - 1 - stack[-1]))return ansjava:
class Solution {public int maximalRectangle(char[][] matrix) {int ans = 0;final int rows = matrix.length;final int cols = matrix[0].length;final int[] heights = new int[cols];Deque<Integer> stack = new ArrayDeque<>();stack.push(-1);for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {// 矩阵转换为柱状图(滚动数组)if (matrix[i][j] == '1') {heights[j] += 1;} else {heights[j] = 0;}while (stack.size() > 1 && heights[stack.peek()] > heights[j]) {// 栈中比当前位置高的那些待确定右边界的下标都可以确定右边界了ans = Math.max(ans, heights[stack.pop()] * (j - 1 - stack.peek()));}// 入栈,等到能够确定右边界时处理stack.push(j);}while (stack.size() > 1) {// 栈中剩余的都是右边没有更低的ans = Math.max(ans, heights[stack.pop()] * (cols - 1 - stack.peek()));}}return ans;}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
这篇关于算法leetcode|85. 最大矩形(rust重拳出击)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








