《xzc最喜欢的二叉树》 部分数据标程 Apare_xzc

《xzc最喜欢的二叉树》 部分数据&标程

题目链接：xzc最喜欢的二叉树

大致展示

输入先序遍历和中序遍历，还原二叉树，并得到后续遍历,求叶子节点的个数，树的最大深度
输入保证每个节点的值各不相同

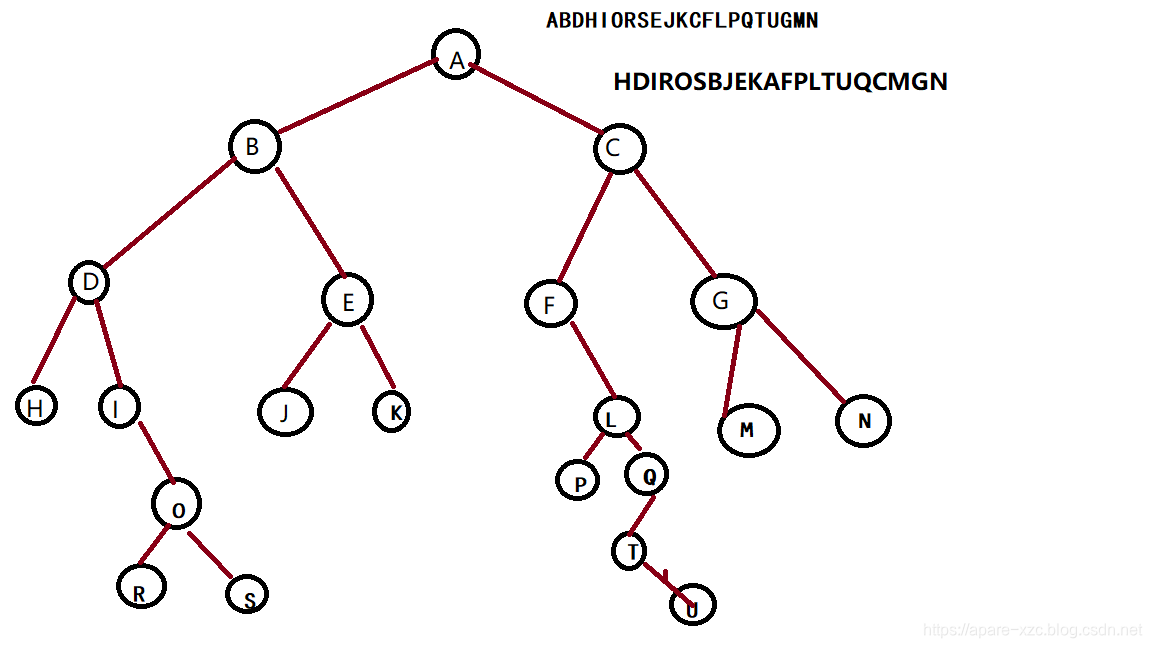
输入的先序遍历为：ABDHIORSEJKCFLPQTUGMN
输入的中序遍历为：HDIROSBJEKAFPLTUQCMGN

先序遍历如下：A B D H I O R S E J K C F L P Q T U G M N
中序遍历如下：H D I R O S B J E K A F P L T U Q C M G N
后序遍历如下：H R S O I D J K E B P U T Q L F M N G C A

节点4(H)是叶子节点
节点7®是叶子节点
节点8(S)是叶子节点
节点10(J)是叶子节点
节点11(K)是叶子节点
节点15§是叶子节点
节点18(U)是叶子节点
节点20(M)是叶子节点
节点21(N)是叶子节点
这棵树有9个叶子节点

这棵树一共有7层，最深的一层在先序遍历中的第一个节点是：18(U)

请按任意键继续. . .

Sample Input

3
3
ABC
BAC
8
ABDFCEGH
BFDACGEH
21
ABDHIORSEJKCFLPQTUGMN
HDIROSBJEKAFPLTUQCMGN

Sample Output

Case #1:
该二叉树的后序遍历为：BCA
该二叉树的叶子节点个数为：2
该二叉树的层数为：2，最深的叶子节点的值为：BCase #2:
该二叉树的后序遍历为：FDBGHECA
该二叉树的叶子节点个数为：3
该二叉树的层数为：4，最深的叶子节点的值为：FCase #3:
该二叉树的后序遍历为：HRSOIDJKEBPUTQLFMNGCA
该二叉树的叶子节点个数为：9
该二叉树的层数为：7，最深的叶子节点的值为：U

标程std.cpp

/*
FileName: std.cpp 
Author: xzc
Date: 2020.1.27 
*/
#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int maxm = 100+10;
char InOrder[maxn],PreOrder[maxn]; //输入的中序遍历和先序遍历 
int Lchild[maxn],Rchild[maxn],fa[maxn],n,cnt; //记录每个节点的左子节点编号，右子节点编号，父节点编号 
map<char,int> pos; 
void dfs();
void getPostOrder(int);
void CountLeaves(int,int&);
void getMaxDeep(int,int,int&,int&);
int main()
{
//	freopen("in.txt","r",stdin);
//	freopen("StdOut.txt","w",stdout); int T;scanf("%d",&T);for(int ca=1; ca<=T; ++ca){if(ca>1) printf("\n");pos.clear();scanf("%d",&n); //以连续字符串的形式读入先序遍历和中序遍历 scanf("%s",PreOrder+1);scanf("%s",InOrder+1);//初始化每个节点左右子节点均为空 memset(Lchild,-1,sizeof(Lchild));memset(Rchild,-1,sizeof(Rchild));fa[1] = 1;for(int i=1;i<=n;++i){   //预处理 pos是一个map:作用：将 pos[InOrder[i]] = i;}cnt = 1; //dfs初始化，先序遍历的第一个节点一定是根节点 dfs(); //得到每个节点Lchild,Rchild和fa的信息 //后序遍历 printf("Case #%d:\n",ca);cout<<"该二叉树的后序遍历为："; getPostOrder(1);printf("\n"); //统计二叉树叶子节点的个数 int cntOfLeaves = 0;CountLeaves(1,cntOfLeaves);printf("该二叉树的叶子节点个数为：%d\n",cntOfLeaves);//求树的层数(最大深度)以及最深的节点 int MaxDeep = 0, MaxDeepLeafID = 0;getMaxDeep(1,1,MaxDeep,MaxDeepLeafID);printf("该二叉树的层数为：%d，最深的叶子节点的值为：%c\n",MaxDeep,PreOrder[MaxDeepLeafID]);} fclose(stdin);fclose(stdout);	return 0;	
} void dfs() //先序遍历中的序号 
{if(cnt==n) return;  //cnt = fa 表示上一个节点 int val = PreOrder[cnt]; //值 int p = pos[val];  //在中序遍历中的位置 int NextVal = PreOrder[cnt+1];int Nextp = pos[NextVal];if(Nextp<p) //cnt+1是cnt的左子节点 {Lchild[cnt] = cnt+1;fa[cnt+1] = cnt;}	else //Nextp > p   //可能该节点是某个节点的右子节点 {int father = -1;int x = cnt; //上一个节点while(true)  //先序遍历的第一个结点必定是树的根节点 {if(Rchild[x]==-1&&Nextp>pos[PreOrder[x]]){father = x;	} if(x==1) break;x = fa[x];	} Rchild[father] = cnt+1;fa[cnt+1] = father;}cnt++;if(cnt==n) return;dfs();
}void getPostOrder(int x)
{if(Lchild[x]!=-1) getPostOrder(Lchild[x]);if(Rchild[x]!=-1) getPostOrder(Rchild[x]);cout<<PreOrder[x];
}void CountLeaves(int x,int& num)
{if(Lchild[x]==-1&&Rchild[x]==-1) num++;if(Lchild[x]!=-1) CountLeaves(Lchild[x],num);if(Rchild[x]!=-1) CountLeaves(Rchild[x],num);
}
void getMaxDeep(int x,int deep,int &ans,int &LeafID)
{if(deep>ans){ans = deep;LeafID = x;}if(Lchild[x]!=-1) getMaxDeep(Lchild[x],deep+1,ans,LeafID);if(Rchild[x]!=-1) getMaxDeep(Rchild[x],deep+1,ans,LeafID); 
}