Uniswap 解析：恒定乘积做市商模型Constant Product Market Maker Model 的Vyper 实作

二. 恒定乘积做市商模型Constant Product Market Maker Model

交易所如果要去中心化、也不使用挂单order book，就需要靠演算法自动算出交易标的的数量与价格，而Uniswap 使用名为恒定乘积的演算法，其来源可追溯自Vitalik 的这篇文章：点我。

公式非常的简单：x * y = k。令交易的两虚拟货币为X 和Y，各自数量为x 和y，两货币数量的乘积x * y 恒等于k，k 值是由第一笔注入的流动性所决定(于 三. 流动性Liquidity解释)。

因此，用∆x 数量的X 币来购买Y 币所能得到的数量∆y、或是为了购买∆y 需要付出的∆x 数量，依照此公式进行计算：(x+∆x)(y-∆y) = k，而交易的价格就是两币量∆x 和∆y 的比。

以下公式用α = ∆x / x 和β = ∆y / y 来表示∆x 和∆y 及XY 两币在交易发生后的新均衡数量：

图一

1. 计入手续费

在Uniswap 进行的每一笔交易都会被收取ρ = 0.003 / 0.3% 的手续费回馈给流动性提供者liquidity provider ，因此要将手续费纳入公式的考量：

图二

上图的公式或许不太直觉，我建议不要从x'ρ 及y'ρ 开始理解，而是从∆x 和∆y 两值开始：手续费ρ = 0.3% 的意思是会从付款中扣掉0.3 %，也就是从∆x 扣。在有手续费的情况下∆x 就变成了(1-ρ)∆x ，若令γ = 1-ρ 则为γ∆x。因此，将图一中的∆x 换成γ∆x，就会得到以下式子：

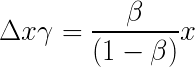
来源：https ://private.codecogs.com/latex/eqneditor.php

将等号左方的γ 移到右方后就得到了图二中的∆x。同理，由于∆y 中的α = ∆x / x ，用γ∆x 代换∆x 就会得到图二中的∆y (有α 的地方乘上γ )。而x' 还有y' 就可以由∆x 和∆y 推出来了！

然而，将图二中得到的x' 和y' 相乘，会得到：

来源：https ://private.codecogs.com/latex/eqneditor.php

也就是说，当有手续费使得γ != 1 /ρ != 0，x'ρ * y'ρ 的值其实会稍微和xy = k 不同：在实作上γ = 0.997 / ρ = 0.003，因此1/γ-1 ≒ 0.003。β = ∆y / y 代表的是换得的Y 币占总量的比例，即使最大值为1，误差也只有1 * 0.003，故可知手续费= 0.3% 对于k 值的影响极小。

2. 程式码结构

了解了基本的公式后，就可以开始研究程式码是怎么撰写的。首先来看各个函式的功能：

• addLiquidity()及removeLiquidity()：转入与转出资金，留到 三. 流动性Liquidity中说明
• getInputPrice()及getOutputPrice()：最主要的函式，用以计算给∆x 所能换得的∆y 数量、以及为了得到∆y 所要支付∆x 的数量。此两函式会被其他负责进行交易、汇币的函式使用
• 三组(eth->Token, Token->eth, Token->Token) 的swap()及transfer()：swap() 的收币人就是付款人、transfer() 的收币人不是付款人而是指定的对象。基本上这两函式就是呼叫getInputPrice() 或是getOutputPrice() 后进行汇币的动作，因此不再多做解释

3. 演算法核心与实作

在研读程式码前，先回顾一下∆x 和∆y 的公式：

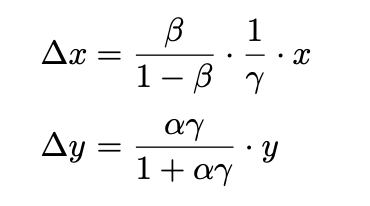
首先我们考虑用∆x 所能购买到的∆y 的getInputPrice()：

什么…就这几行程式码？是的。

以上的程式码和公式表达方式不同，因此先将α = ∆x / x 和β = ∆y / y 代换回来并将上下同乘x：

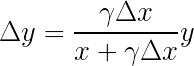
来源：https ://private.codecogs.com/latex/eqneditor.php

由于γ = 0.997，可以将上下同乘1000 后得到：

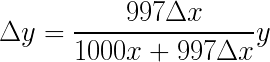
来源：https ://private.codecogs.com/latex/eqneditor.php

接着就能来对照程式码了：

• (109行) numerator : input_amount是欲支付的X 币数量∆x、output_reserve是Y 币数量y，再乘上997 后就是等式右边的上方(= 997∆xy)
• (110行) denominator : input_reserve是X 币的数量，乘上1000 再加上刚刚算过的997∆x，就得到了等式右边的下方(= 1000x + 997∆x)
• 此处要注意的是Vyper 的除法是无条件舍去，等同于floor() 函式。这会不会造成严重的影响呢？如果熟悉ERC20 的人应该记得，在发币时输入的四个参数中有一个参数代表小数点的位数，如同下方程式码中的2 代表最后两位在小数点后。举例来说，当getInputPrice() 收到1234567 为这个币的input_amount时，代表使用者拥有的币的数目实际上是12345.67。因此，即使将结果舍去0.67 后的数字，影响真的不大，况且如果不舍去而选择无条件进位，那代表交易所反而要亏损一点点啦，太佛心了吧xD 有兴趣者可以看看审计报告的内容，有更详细地去定义这些误差所影响的范围！

再来我们看若要购买∆y 需要付出多少∆x 的getOutputPrice()。

一样先将α = ∆x / x 、β = ∆y / y 和γ = 0.003 代换并上下同乘1000y 得到：

来源：https ://private.codecogs.com/latex/eqneditor.php

我们已经看过getInputPrice() 一次了，所以应该能发现第122–124 行得出的结果和上式相同。要注意的是这边的结果反而是无条件舍去后直接+1，因为这是在计算使用者要付多少∆x 才能购买到∆y，为了不让交易所亏只能选择请使用者多付一点点。

4. 段落小结

以上就是撇除汇币等函示，恒定乘积做市商的Vyper 实作，没错就这样而已！Uniswap 之所以可以做到低gas 消耗就是因为这个演算法本身就非常简单，所需的运算也就是两三次乘除法而已！

不过我们还没结束，接下来要谈谈如何投入资金/注入流动性，而这部分也包含了决定k 值的精妙机制！

三. 流动性Liquidity

流动性指的是交易市场中能够交易的资金/标的物的量。使用自动做市商(AMM) 而非挂单的最大好处就是市场一定会有流动性，而缺点就是如果交易量越大就会造成越大的滑点Slippage，意思就是交易价格变动会越大、得到的价格越差。

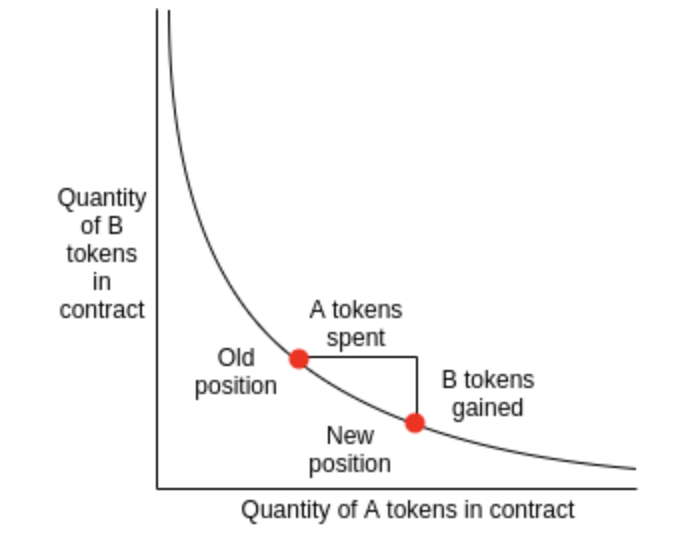
来源：https ://ethresear.ch/t/improving-front-running-resistance-of-xyk-market-makers/1281

我们可以用上面提到的V 文章中的图片来迅速带过，毕竟有关注Uniswap 的读者大概都已经看过这图很多次了。

当要兑换的币的数量越大/占比越重，例如：20% Y 币的流动性，就会造成要付出比兑换少量时极为不对称的高额X 币。

接着我们要来探讨注入流动性的原则，依照市场是否已经有流动性而区分为两种情形：

1. 第一笔流动性注入、决定k 值

以下程式码是addLiquidity() 函式中46-48, 51, 及64-74 行。当市场上还没有任何流动性时，不会满足第51 行而是进入64 行的else。

在第65 行我们可以看到msg.value ≥ 10¹⁰，以及在67 行token_amount就是其中一个输入值max_tokens。这边代表的是第一个注入流动性的使用者可以自行决定要注入多少Ether (≥ 10¹⁰) (= x) 以及相应的币的数量(= y)，也就是上方提到的k 值(= x* y)，在本例的X 币就是Ether。(本处先不解释剩余的程式码，留到2. 除了第一笔以外的情况)

那么问题来了：第一个注入流动性的人要怎么决定提供各自多少的两种币呢？最好的办法是依照当时两币的市价比，让两者的价值(数量* 价格) 相同，例如：当1 Ether 的价格为100 Dai，注入1 Ether 以及100 Dai 是最好的，因为两种币的总价值是一样的，以下举例说明原因。

当1 Ether 市价为100 Dai 时，假设第一人决定注入1 Ether 和50 Dai (k = 50)，总价值为150 Dai，我们考虑两种兑换方法：

1. Ether -> Dai：用0.1 Ether 来购买Dai，依照上方公式(1+0.1)(50-y) = 50 可得y ≒ 4.55，也就是说得到的价格是0.1 Ether = 4.55 Dai，远低于市价0.1 Ether = 10 Dai，相信没有人这么傻~
2. Dai -> Ether：用2 Dai 来购买Ether，依照上方公式(1-x)(50+2) = 50 可得x ≒ 0.038，也就是说得到的价格是2 Dai = 0.038 Ether，高于市价2 Dai = 0.02 Ether，那么眼尖的人就会立刻冲来套利了xD

那么即使如此，第一人有所损失吗？当然有！假设路人A 手上有30 Dai (= 0.3 Ether)，A 看到机会后就把30 Dai 全换成Ether：(1-x)(50+30) = 50 可得x = 0.375，大于原本持有的Dai 的价值0.3 Ether。此时，第一人即使立刻抽出现存的全部资金Ether = 0.625 及Dai = 80，总价值也只剩下142.5 Dai，比起原本的150 Dai 还少。以上的计算还有手续费没有纳入考量，但也只有30 Dai 的0.3% = 0.09 Dai。

由上例可知，第一位提供流动性的人为了避免自己的损失，确实得依照当时两币的市价比去提供相应的数量。杰克，这真是太神奇了0…0

2. 除了第一笔以外的情况

如果市场已经有流动性，使用addLiquidity() 来注入流动性就会进入第51 行的if。

来源：https ://github.com/Uniswap/uniswap-v1/blob/master/contracts/uniswap_exchange.vy

• (53行) eth_reserve : 由于使用者已经透过函式addLiquidity() 将钱汇入了合约，因此将合约所拥有的Ether 数量self.balance (= x + ∆x) 减去使用者汇入的钱msg.value (= ∆x)，得到使用者汇钱之前合约内所拥有的Ether 数量(= x)
• (54行) token_reserve : self.token是一个喂入币地址的ERC20 instance；透过呼叫ERC20 的函式balanceOf()即可查出合约所拥有的Y 币的数量(= y)
• (55行) token_amount : 透过将合约所拥有的Y 币的数量token_reserve (= y) 乘上使用者汇入的钱msg.value (= ∆x) 对合约原本拥有的Ether 数量eth_reserve (= x) 的比例，代表使用者应该相应地注入多少Y 币(∆y = y * ∆x / x)。除法一样是无条件舍去
• (56行) liquidity_minted : 将原本交易所中的总流动性total_liquidity乘上增加的比率msg.value / eth_reserve (= ∆x / x) ，代表增加的流动性，随后会在第58 行记录下来
• (60行) transferFrom()函式将使用者应付的Y 币数量token_amount (= ∆y) 汇入当前合约，就完成了流动性的注入。小提示：智能合约中的assert()会确保函式内的条件如果失败就整笔交易transaction直接取消，因此只要传入的参数已经被计算好，于60 行再进行transferFrom()其实与放在前面并没有太大的差别

以上就是注入流动性的大致实作内容。取出资金removeLiquidity() 其实与addLiquidity() 的做法大同小异，因此就不再赘述。

四. 结语

呼，真的累。恒定乘积做市商模型的概念虽然简单，但解释起来还是挺复杂的！其实本文并未着墨于审计报告中的主要议题：评估因为整数除法(不使用浮点数) 而造成的误差范围，因为讲起来非常复杂、也不是真的这么需要知道。不过，恰巧就是这些程式码的细节有可能让程式产生预期之外的结果！因此，对于有兴趣了解该如何去分析智能合约整数除法的读者，可以研究一下；而Uniswap 的程式码因为是用Vyper 实作，可读性非常高、同时也不难，因此也非常值得打开来看看、甚至动手实作自己的版本！

最后，如果本文有任何错误，请不吝提出，我会尽快做修正；而如果我的文章有帮助到你，可以看看我的其他文章，欢迎一起交流:)