SBD算法详解与相关python代码

本文为原创，转载请注明出处，谢谢！

https://blog.csdn.net/qq_22135585/article/details/108830390

当涉及到延时情况，如kpi数据，在判断两两特征相关性的时候就不得不考虑SBD算法了。

通过SBD算法，我们可以在不清楚延迟的情况下找到两组数据的相关性，以下来进行详细讲解。

SBD算法

       对于时间序列X()及时间序列Y()，两序列间的存在时延为s的关系，计算两条曲线相似度的SBD距离算法如下：

                  NCC(X,Y)=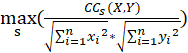

                  SBD(X,Y)=1-NCC(X,Y)

      其中，NCC为序列X,Y的标准化互相关系数，NCC的取值范围在-1到1之间，与皮尔森相关系数类似。 所以最终计算的SBD算法结果在0到2之间，越靠近0时，两组数据相关性越强。当SBD为0时，说明序列X,Y波动曲线一致，为同一序列。在后面的代码中，考虑到输出NCC的值更有统计学意义，因此就直接输出NCC了。

      由于SBD算法计算的是距离，因此在计算距离前我们需要进行Z-score归一化处理。

      细心的朋友可以发现，当延迟为0时，归一化后该算法中的ncc值相当于在计算皮尔森相关系数。

      SBD算法的缺点就是计算量大，在类似KPI场景数据量庞大的时候，SBD算法可能无法得到支撑。

      但是，在涉及告警根因分析等问题时，SBD能自动的判断出延迟的位数。

      我们可以通过对比延时的大小，从而准确地判断出故障根因。

   注意事项：使用算法时切记要在告警点附近使用！！注意避开周期性的数据，不然可能会出现关联偏差。

   好了，废话不多说，这里为大家分享下我写的算法函数：

#SBD距离算法
def calcSBDncc(x,y,s):assert len(x)==len(y)assert isinstance(s,int)length_ = len(x)pow_x = 0pow_y = 0ccs = 0for i in range(length_-s):ccs +=  x[i+s]*y[i]pow_x += math.pow(x[i+s],2)pow_y += math.pow(y[i],2)dist_x =math.pow(pow_x,0.5)dist_y =math.pow(pow_y,0.5)dist_xy = dist_x*dist_yncc = ccs/dist_xyreturn ncc
def calcSBD(x,y,s=None):assert len(x)==len(y)if  s==None:length_ = len(x)ncc_list = []for i in range(int(length_*0.5)):  #这里的0.5保证至少有一半的数据用于相关性的计算了ncc_list.append(calcSBDncc(x,y,i))ncc = max(ncc_list)delay = ncc_list.index(max(ncc_list))sbd = 1 - nccelse:ncc = calcSBDncc(x,y,s)delay = s  #作为告警延时数传递sbd = 1 - ncc #sbd 数据在0-2之间，这里还是返回ncc 更适合相关性解释return ncc,delay

第一次写原创，请多指教。如果有不明白的地方，欢迎有兴趣的朋友留言交流！