动态规划法C++实现最大k乘积问题

最大K乘积问题
问题描述
设I是一个n位十进制整数。如果将I划分为k段，则可得到k个整数。这k个整数的乘积称为I的一个k乘积。试设计一个算法，对于给定的I和k，求出I的最大k乘积。
例如十进制整数 1234 划分为 3 段可有如下情形：
1 × 2 × 34 = 68
1 × 23 × 4 = 92
12 × 3 × 4 = 144
编程任务
对于给定的I 和k，编程计算I 的最大k 乘积。
数据输入
输入的第1 行中有2个正整数n和k。正整数n是序列的长度；正整数k是分割的段数。接下来的一行中是一个n位十进制整数。（n<=10）
结果输出
计算出的最大k乘积。
输入文件示例 输出文件示例
input.txt output.txt
3 2
312 62

问题分析
首先用反证法证明最大k乘积问题具有最优子结构性质，从而证明该题目适合使用动态规划法：
（1）假设n位十进制整数I的最大k乘积记为f（n，k），前k-1段总共是m位，且1<=m<n，则最后一段为n-m位，用I(m,n-m)表示从第m位开始的最后n-m位十进制数,则f(n，k)=f(m,k-1)*I(m,n-m).
（2）现在我们假设前面m位十进制整数的最大k-1乘积不是f(m,k-1)，而是H(m,k-1),则有H(m,k-1)>f(m,k-1), 左右两边同时乘以I(m,n-m)得H(m,k-1)*I(m,n-m)>f(m,k-1)*I(m,n-m)=f(n,k) 即f(n,k)不是I的最大K乘积与最初的假设相矛盾。
(3)所以f(m,k-1)是前面m位十进制整数的最大k-1乘积，即最大k乘积问题具有最优子结构性质。这说明可以使用动态规划来求解。
算法步骤：
（1）
1.1设tempArr(h,k) 表示: 从第h位到第k位所组成的十进制数
1.2设dp(i,j)表示前i位(1-i)分成j段所得的最大乘积,
1.3arr数组储存给定的n个数字 ；
1.4首先将连续数字第i位到第j位表示的十进制数放在tempArr数组，dp[i][j]代表前i位有j个乘号。
（2）写出动态方程：
如果只分成一段，那么dp[i][1]=tempArr[1][i];
否则： 前i位(1~i)数字分j组乘积的最大值等于分为j-1组的结果再乘以一个后面剩下的数字组成所代表的的十进制数。
dp[i][j]=max(dp[i][j],dp[k][j-1]*tempArr[k+1][i]); 1<=k<i;
（3）最终的结果dp[n][k-1]即为最大k乘积
代码实现：

#include<iostream>
#include <fstream>
#include <string>
#include <sstream>
#include<algorithm>
#include<vector>
#define MAX 20
using namespace std;//数字的位数
int  n = 0;
//分成k段
int k = 0;
//给定的数字
int value = 0;
//存储给定数组的每一个数字
int* arr = NULL;
//存储k乘积最大值
int arr2D[MAX][MAX];
//临时存放第i个到第j个数字表示的十进制数
int tempArr[MAX][MAX];
/*
读取给定的data.txt文件的数据
读取第一行的n , k
第二行的数字 并将每一个数组存储到arr数组中
*/
void readTextData()
{//data.txt为你自己的输入文件路径ifstream ifs("data.txt", ios::in | ios::binary); // 改成你要打开的文件if (ifs.is_open()) {//读取字符的缓冲容器char buf[100];//临时装载读取的元素string s = "";//控制是否读取结束bool fla = false;int count = 0;memset(buf,' ',100);while (!ifs.eof()){//读取文本内容到缓冲容器中ifs.read(buf, 100);for (int i = 0; i < 100; i++) {if (!isspace(buf[i])){//读取遇到空格前的数据，比如" 12 3  4"，分别读取为：s="12",s="3",s="4"s += buf[i];}else {if (count  == 0){n = atoi(s.c_str());arr = new int[n];count++;s = "";}else if (count == 1) {k = atoi(s.c_str());count++;s = "";}else if (count == 2){if (buf[i] == '\r' || buf[i] == '\n'){continue;}else{value = atoi(s.c_str());for (int j = 0; j < s.length(); j++){arr[j] = s[j] - 48;}fla = true;break;}}}}if (fla == true){break;}}cout << "输入的数据为：";for (int  i = 0; i < n; i++){cout << arr[i];}cout << endl;ifs.close();}else {cout << "打开文件失败" << endl;}}/*
@to do:将读取到的value从第i个到第j个数字表示的十进制值存储到一个数组中
*/
void init()
{for (int i = 1; i <= n; i++){//给数组对角线赋值tempArr[i][i] = arr[i - 1];}for (int i = 1; i <= n; i++){for (int j = i + 1; j <= n; j++){//获取每个第i到第j位表示的十进制数tempArr[i][j] = tempArr[i][j - 1] * 10 + tempArr[j][j];}}}
int getValue() 
{//枚举前i个数字 for (int i = 1; i <= n; i++)  {//枚举乘号个数  for (int j = 0; j < i; j++){if (j == 0){arr2D[i][j] = tempArr[1][i]; continue;}//枚举乘号位置   for (int k = 1; k < i; k++){//找到最大的k乘积arr2D[i][j] = max(arr2D[i][j], arr2D[k][j - 1] * tempArr[k + 1][i]);}}}//返回最终结果return arr2D[n][k-1];
}int main()
{readTextData();init();int result = getValue();cout <<"最大"<<k<<"乘积结果为："<< result << endl;system("pause");return 0;
}

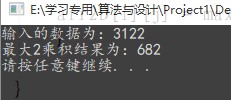
当data.txt文件输入为：

输出结果：

实验分析：
根据算法我们知道使用了一个一维数组arr，两个二维数组tempArr和dp，所以该算法的空间复杂度为O(nn)，在函数init（）初始化过程中，使用了两个嵌套的for循环，时间复杂度为O(nn)，在getValue（）函数中，使用了三个for循环，时间复杂度为O（nnn）,所以该算法的时间复杂度为O（nnn）