查找算法 —— 斐波拉契查找法

本文主要是介绍查找算法 —— 斐波拉契查找法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、介绍

        斐波拉契查找法是以分割范围进行查找的，分割的方式是按照斐波拉契级数的方式来分割。好处是：只用到加减运算，计算效率较高一些。

       要使用斐波拉契查找首先需要定义一颗斐波拉契查找树，建立规则如下：

       1.斐波拉契树的左右子树均为斐波拉契树。

       2.当数据个数n确定时，若想确定斐波拉契树的层数k值，就必须找到一个最小的K值，使得斐波拉契层数的Fib（k+1）>= n+1.

       3.斐波拉契树的树根一定是一个斐波拉契树，且子节点与父节点差值的绝对值为斐波拉契数。

       4.当k>=2时，斐波拉契树的树根为Fib(k),左子树为（k-1）层斐波拉契树（其树根为Fib(k-1)）,

右子树为（k-2）层斐波拉契树（其树根为Fib(k) + Fib(k-2)）。

       5.若n+1的值不为斐波拉契数的值，则可以找出存在一个m使用Fib(k+1)-m = n+1，m=Fib(k+1)-(n+1),再按斐波拉契树的建立原则完成斐波拉契树的建立，最后斐波拉契树的各节点减去差值m即可，并把小于1的节点去掉。

      可以先罗列一部分斐波拉契数的值，如下：

 Fib(0) = 0, Fib(1) = 1, Fib(2) = 1, Fib(3) =2, Fib(4) = 3，

 Fib(5) = 5, Fib(6) = 8, Fib(7) = 13,  Fib(8) = 21, Fib(9) = 34,

      接下来第一种情况时n+1的值是斐波拉契数的值，假设就是数1~33，也就是n=33,那么n+1 = 34,可以根据Fib(k+1) >= n+1 得出 k的值为8，则可以建立斐波拉契树，如下：       

  第二种情况就是n+1的值不是斐波拉契数的值，假设n=10,那么n+1 =11，不是斐波拉契数，按照第五条规则，可以找出一个值m,使Fib(k+1) - m = n+1成立，则Fib(k+1)=13,则m=2, k=6,按照规则建立的斐波拉契树如下：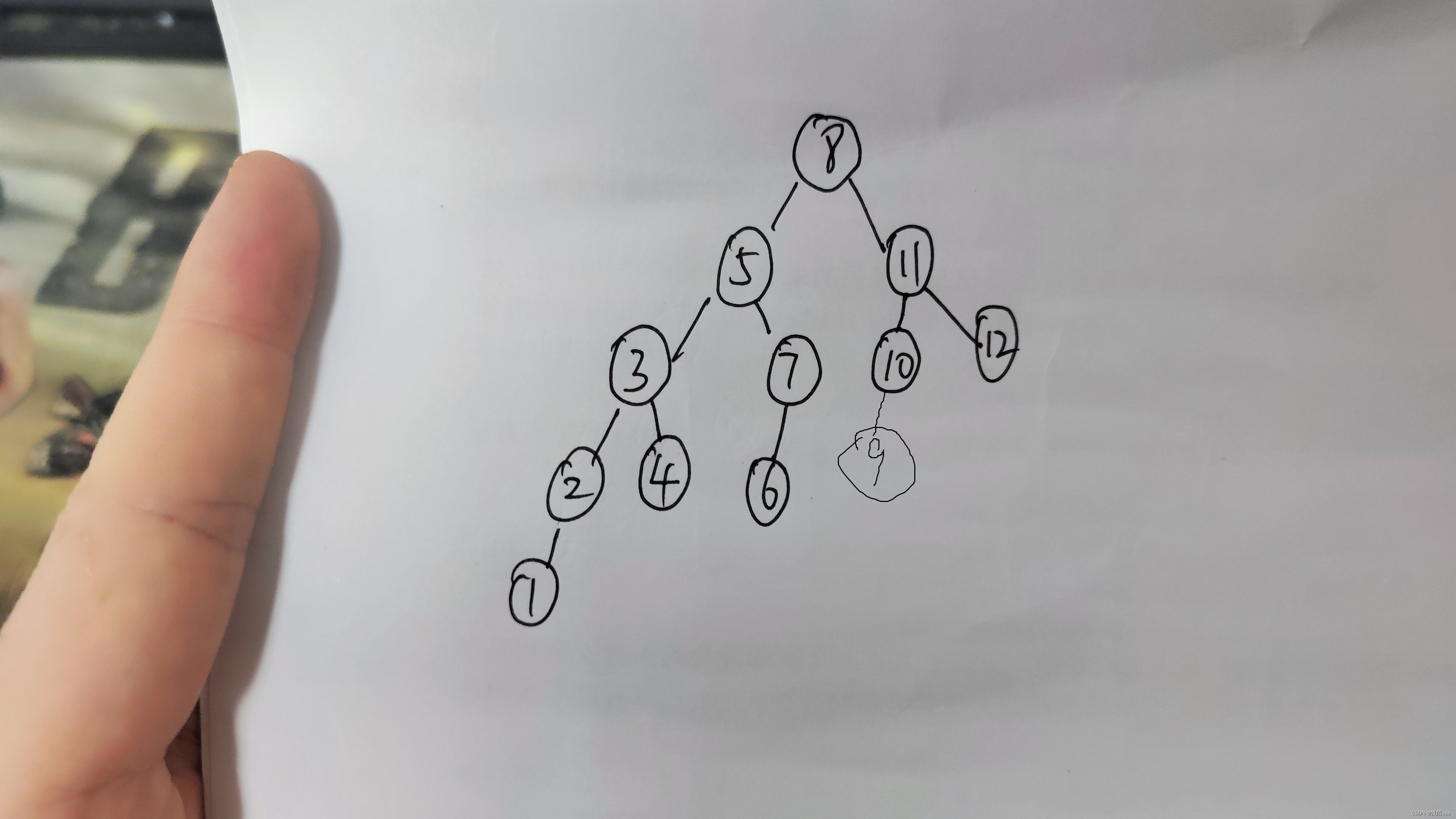

各节点减去m,并把小于1的节点去掉之后得到

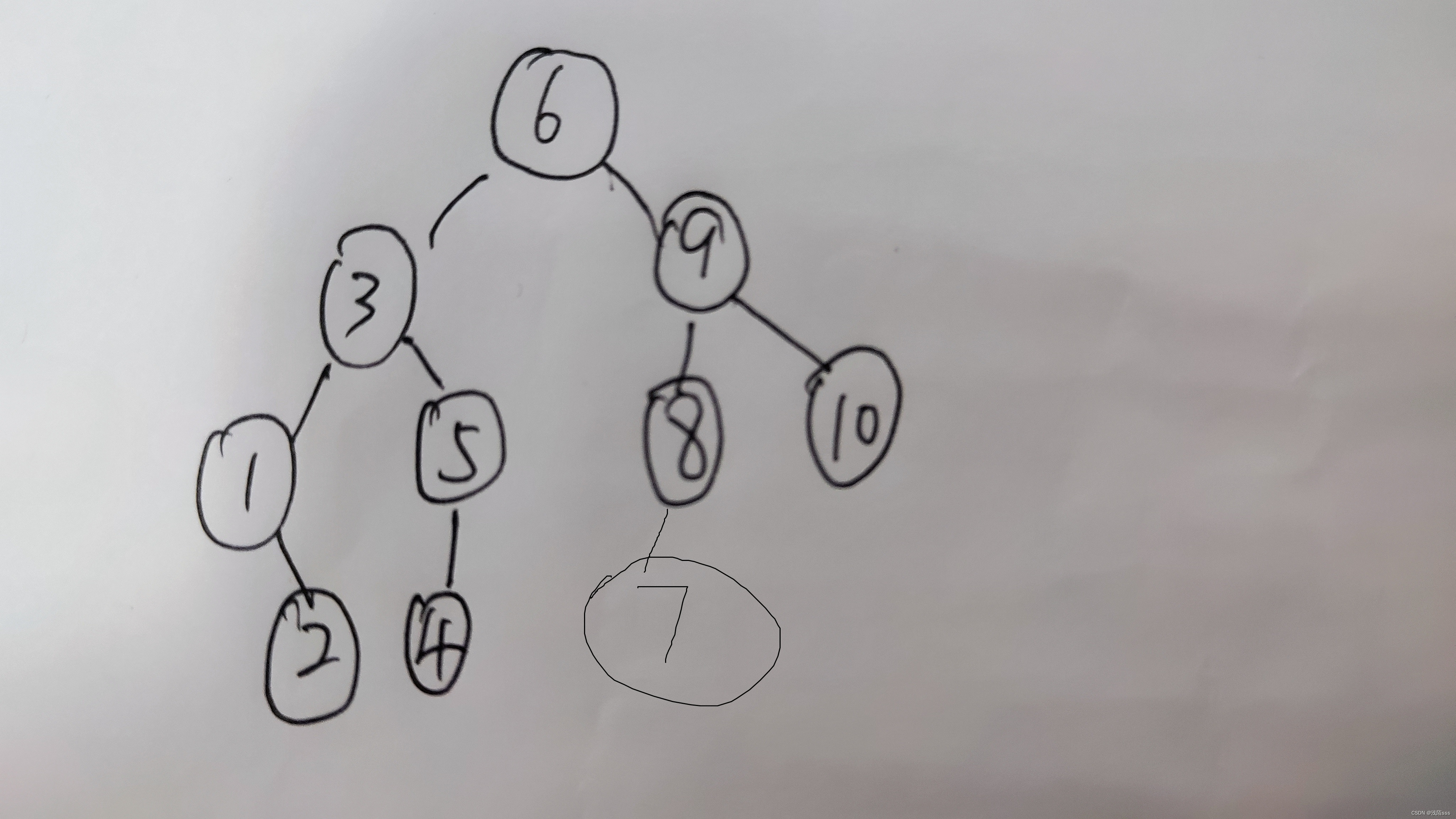
斐波拉契查找法步骤首先将要查找的数与树根Fib(k)比较，如果相等这个数就是Fib(k),如果比Fib(k)小则，数在1到Fib(k)-1之间，如果比Fib(k)大，则这个数在Fib(k)+1到Fib(k+1)-1之间。

二、建立Fib树代码

1.首先先生成Fib数储存起来，避免每次查找都要计算一遍：

void FibCalc(int n)
{   fibls.Add(0);for (int i = 1; i < n; i++){if (i < 3){fibls.Add(1);}else{fibls.Add(fibls[i-1] + fibls[i-2]);} }
}

2.然后判断一个数是不是Fib数并且找到一个比这个数大或者相等的Fib数

 bool LookUpFibAndIsFib(int val, out int ksum1){ksum1 = -1;if (val < 0){Debug.LogError("输入的值不能小于0");return false;}for (int i = 0; i < fibls.Count; i++){if (val == fibls[i]){ksum1 = i;return true;}else if(val < fibls[i]){ksum1 = i;return false;}}Debug.LogError("没有匹配到K");return false;}

 3，生成Fib树

  void GenerateFibTree(Node node, int k,int val){if (k - 2 < 0) return;int fibNum = node.Data - fibls[k - 2];if (fibNum == node.Data) return;if (node.Data != 1){node.LeftNode = new Node();node.LeftNode.Data = fibNum;node.LeftNode.PNode = node;}int fibNumR = node.Data + fibls[k - 2];if (fibNum > 1 && fibNumR != root.Data){if (fibNumR != node.PNode.Data || node.PNode == null){if (node.PNode.PNode != null && fibNumR != node.PNode.PNode.Data){node.RightNode = new Node();node.RightNode.Data = fibNumR;node.RightNode.PNode = node;}if (node.PNode.PNode == null){node.RightNode = new Node();node.RightNode.Data = fibNumR;node.RightNode.PNode = node;}}}if (node.LeftNode != null)GenerateFibTree(node.LeftNode, k - 1, val);if (node.RightNode != null)GenerateFibTree(node.RightNode, k - 2, val);}

 4.在需要减去m的情况下：

 void FibTreeMinusM(int m,Node node){if (node.LeftNode != null){node.LeftNode.Data -= m;FibTreeMinusM(m, node.LeftNode);if (node.LeftNode.Data < 1)node.LeftNode = null;}if (node.RightNode != null){node.RightNode.Data -= m;FibTreeMinusM(m, node.RightNode);if (node.RightNode.Data < 1)node.RightNode = null;}}

5.最后按照输入的数值生成Fib树

   void FibLookUpArithmetic(int val){int ksum1 = 0;if (LookUpFibAndIsFib(val+1, out ksum1)){int k = ksum1 - 1;InitGenerateFibTree(k,val);}else{int k = ksum1 - 1;InitGenerateFibTree(k, val);int m = fibls[ksum1] - (val + 1);root.Data -= m;FibTreeMinusM(m, root);}}

 完整代码：

using System.Collections.Generic;
using UnityEditor.Experimental.GraphView;
using UnityEngine;
using UnityEngine.Rendering;public class LookUpArithmetic : MonoBehaviour
{List<int> fibls;Node root;void Start(){fibls = new List<int>(30);FibCalc(30);FibLookUpArithmetic(10);}void FibLookUpArithmetic(int val){int ksum1 = 0;if (LookUpFibAndIsFib(val+1, out ksum1)){int k = ksum1 - 1;InitGenerateFibTree(k,val);}else{int k = ksum1 - 1;InitGenerateFibTree(k, val);int m = fibls[ksum1] - (val + 1);root.Data -= m;FibTreeMinusM(m, root);}}bool LookUpFibAndIsFib(int val, out int ksum1){//首先判断是否是一个Fbi数和找到一个Fbi数两步可以合并为一步ksum1 = -1;if (val < 0){Debug.LogError("输入的值不能小于0");return false;}for (int i = 0; i < fibls.Count; i++){if (val == fibls[i]){ksum1 = i;return true;}else if(val < fibls[i]){ksum1 = i;return false;}}Debug.LogError("没有匹配到K");return false;}void FibCalc(int n){   fibls.Add(0);for (int i = 1; i < n; i++){if (i < 3){fibls.Add(1);}else{fibls.Add(fibls[i-1] + fibls[i-2]);} }}void InitGenerateFibTree(int k, int val){root = new Node();root.Data = fibls[k];root.LeftNode = new Node();root.LeftNode.Data = fibls[k] - fibls[k - 2];root.LeftNode.PNode= root;GenerateFibTree(root.LeftNode, k - 1, val);root.RightNode = new Node();root.RightNode.Data = fibls[k] + fibls[k - 2];root.RightNode.PNode = root;GenerateFibTree(root.RightNode, k - 2, val);}void GenerateFibTree(Node node, int k,int val){if (k - 2 < 0) return;int fibNum = node.Data - fibls[k - 2];if (fibNum == node.Data) return;if (node.Data != 1){node.LeftNode = new Node();node.LeftNode.Data = fibNum;node.LeftNode.PNode = node;}int fibNumR = node.Data + fibls[k - 2];if (fibNum > 1 && fibNumR != root.Data){if (fibNumR != node.PNode.Data || node.PNode == null){if (node.PNode.PNode != null && fibNumR != node.PNode.PNode.Data){node.RightNode = new Node();node.RightNode.Data = fibNumR;node.RightNode.PNode = node;}if (node.PNode.PNode == null){node.RightNode = new Node();node.RightNode.Data = fibNumR;node.RightNode.PNode = node;}}}if (node.LeftNode != null)GenerateFibTree(node.LeftNode, k - 1, val);if (node.RightNode != null)GenerateFibTree(node.RightNode, k - 2, val);}void FibTreeMinusM(int m,Node node){if (node.LeftNode != null){node.LeftNode.Data -= m;FibTreeMinusM(m, node.LeftNode);if (node.LeftNode.Data < 1)node.LeftNode = null;}if (node.RightNode != null){node.RightNode.Data -= m;FibTreeMinusM(m, node.RightNode);if (node.RightNode.Data < 1)node.RightNode = null;}}
}class Node
{public Node LeftNode;public Node RightNode;public int Data;public Node PNode = null;
}

如有不足之处，欢迎指正。

参考书籍：

清华大学出版社-图书详情-《图解数据结构--使用C#》 (tsinghua.edu.cn)

这篇关于查找算法 —— 斐波拉契查找法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---