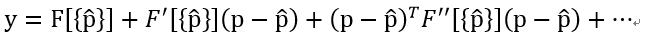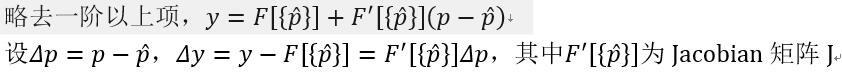扰动算法(零星整理)模型构建

1.很多论文都在说克服扰动算法初始值选择的局限性，也就是结果值的估计对扰动算法求得最终结果影响很大。
2.一般应用于模型重建中，是一种比较有效的算法。
3.模型求解问题涉及正问题和逆问题。

其中正问题求解方法为 Arridge S R, Hebden J C. Optical imaging in medicine (2):
Modelling and reconstruction [J]. Physics in Medicine and
Biology, 1997, 42(5): 841 - 853.有限元法比较常用于复杂几何形状。
逆问题求解方法：解析法、反投影法、线性方法、非线性方法
 Arridge S R. Optical tomography in medical imaging [J].
Inverse Problems, 1999, 15(2): R41 - R93.
 Arridge S R. Photon-measurement density-functions (1):
Analytical forms [J]. Applied Optics, 1995, 34(31): 7395
- 7409.
 Jiang H B, Paulsen K D, Osterberg U L, et al. Optical
image reconstruction using frequency-domain data:
Simulations and experiments [J]. J Opt Soc Am A, 1996,
13(2): 253 - 266.

4.扰动方法是线性方法，理论基础为Taylor展开，在真实解附近进行迭代，直至迭代结果满足误差允许范围。这里说的在真实解附近迭代的真实解释猜测值，用猜测值接近真实解。

5.通过上面可以看出初始预测值对整体影响较大，当和真实偏离过大时，无法收敛。

6.优化，在迭代之前进行一次，为了更快得到想要的解。

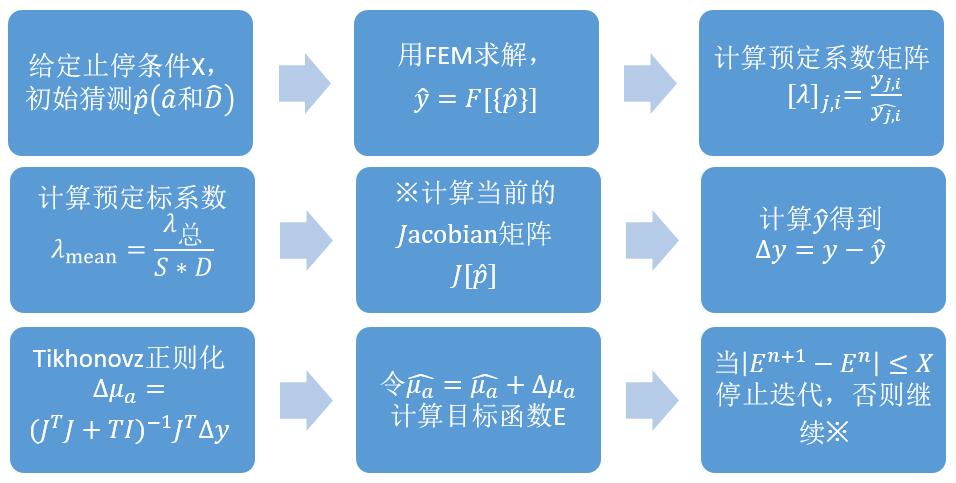
7.基本步骤--最终目的E是整个（S,D）矩阵的最小二乘，即每点与前一点的差再求平方和。

8.雅克比求解有标准方法、伴随源法、直接法、扰动法。
这里讨论一下用扰动法进行求解。
依次对K个参数进行扰动，（这里的pk都是来自猜测值）pk→pk+△pk，令△pk=Tpk，T在实际当中为很小的数，例如0.00000001，主要是为了迭代考虑的小变化。当pk变化后，我们的矩阵（S,D）也发生了相应的变化，记做△（S,D），那么我们可以采用近似的方法，推导出来关于每个参数p的梯度了。△（S,D）/△pk。
当所有的p都求解完成后，我们的k个雅克比矩阵就找到了，总共有S*D*k个元素。

参考文献

基于扰动算法的组织光学断层图像重建_奉华成