本文主要是介绍信息学奥赛初赛天天练-80-NOIP2015普及组-基础题5-错位排列、二叉树、完全二叉树、叶子节点、完全二叉树叶子节点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
NOIP 2015 普及组 基础题5
21 重新排列 1234使得每一个数字都不在原来的位置上,一共有( )种排法
22 一棵结点数为 2015的二叉树最多有( )个叶子结点
2 相关知识点
1) 错位排列
考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)
错排问题最早被尼古拉·伯努利和欧拉研究,因此历史上也称为伯努利-欧拉的装错信封的问题。
这个问题有许多具体的版本,如在写信时将n封信装到n个不同的信封里,有多少种全部装错信封的情况?
又比如四人各写一张贺年卡互相赠送,有多少种赠送方法?自己写的贺年卡不能送给自己,也是典型的错排问题
例题
有99封信,装到99个信箱中,正确的装法是,每封信装到正确的信箱中,即1号信装1号信箱,2号信装2号信箱
每封信都恰好装错的装法一个有多少种?

解析
D[i]表示i封信进行错排
此题需要计算D[99]
通过枚举可知,D[1]=0,D[2]=1,D[3]=2
此题可分2步
第1步
1 把信放入信箱,第1个信箱可以放2~99总共n-1封,即98封信,具体如下

第2步
2 要求装错,1号信不能放入1号信封,除1号信,其他都可以放入1号信封
考虑3号放入1号信封,此时分两种情况
1号信放入3号信和1号信不放入3号信箱2种情况
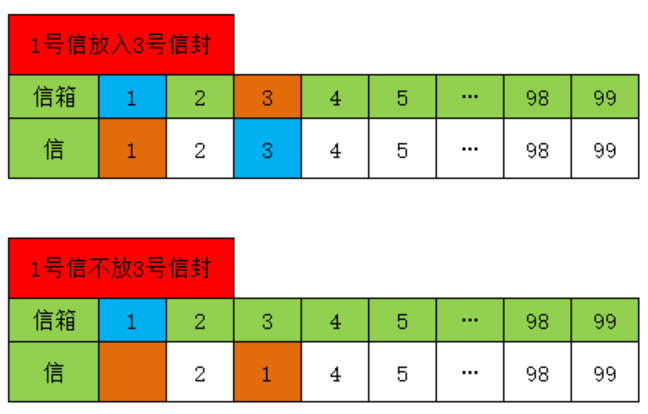
1号信放入3号信封时
1号信和3号信分别3号信封和1号信封,剩余2,4,5...99封信和2,4,5...99个信箱进行错排
满足97封信进行错排即D[n-2]=D[97]1号信不放3号信封时
此时3号信已经放入1号信封,不需要考虑3号信和1号信封
把1号替换到3号信,此时1号信不能放入3号信封,观察信2,1,4,5...99和信封2,3,4,5...99,满足错排
98封信进行错排,这种情况错排D[n-1]=D[98]
根据乘法原理,所以错排的递推公式为
D[n] = (n-1) * (D[n-1] +D[n-1])
D[99]=98 * (D[98] + D[97] )
由前面枚举可知
D[1]=0,D[2]=1,D[3]=2
推出以下错排
D[4]=(4-1) * (D[4-1] + D[4-2])=3*(D[3]+D[2])=3 * (2+1)= 9
D[5]=(5-1) * (D[5-1] + D[5-2])=4*(D[4]+D[3])=4 * (9+2)= 44
2) 树的相关概念
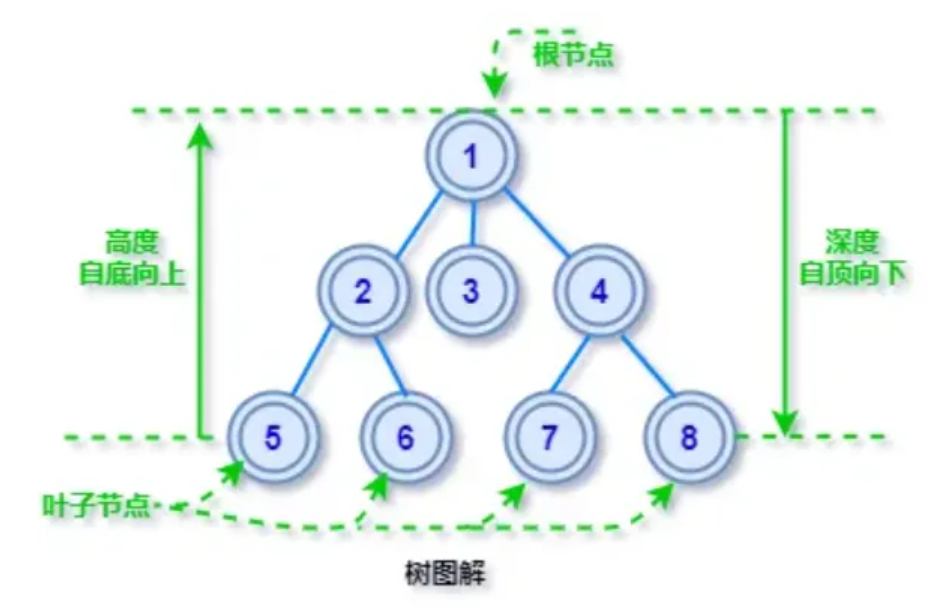
根节点
在一颗树形结构中,最顶层的那个节点就是根节点了,所有的子节点都源自它发散开来。
父节点
树的父子关系和现实中很相似,若一个节点含有子节点,则这个节点称为其子节点的父节点。
叶子节点
直观来看叶子节点都位于树的最底层,就是没有分叉的节点,严格的定义是度为 0 的节点叫叶子节点。
非叶节点
在树中的所有节点,除去叶子节点都为非叶节点
二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒
例如下面是一棵二叉树
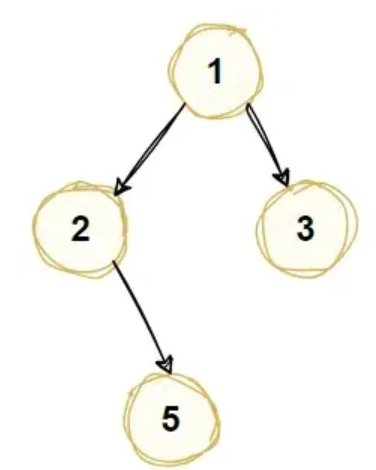
完全二叉树
除了最下层,其他每层都饱满,去除最后一层是一棵满二叉树,最下层的结点都集中在该层最左边的若干位置上
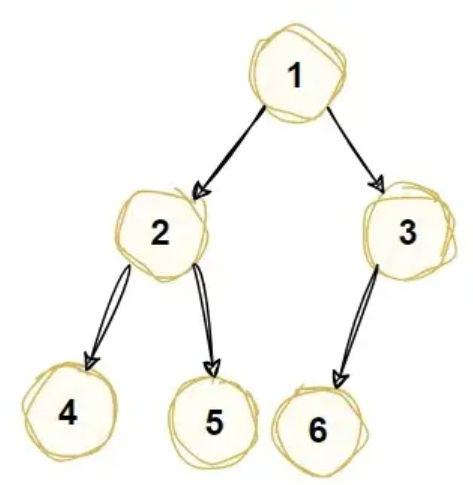
完全二叉树最后1层叶子节点的数量
包括最后1层所有节点和倒数第2层的叶子节点数量
上图如果3没有子节点,也为叶子节点
3 思路分析
21 重新排列 1234使得每一个数字都不在原来的位置上,一共有( 9 )种排法
分析
根据错排公式
D[n] = (n-1) * (D[n-1] +D[n-1])
由前面枚举可知
D[1]=0,D[2]=1,D[3]=2
推出以下错排
D[4]=(4-1) * (D[4-1] + D[4-2])=3*(D[3]+D[2])=3 * (2+1)= 9
22 一棵结点数为 2015的二叉树最多有( 1008 )个叶子结点
分析
二叉树是每个节点最多有两个子节点的树结构。通常,我们称子节点为左子节点和右子节点。
为了最大化叶子节点的数量,我们应该尽量让每个非叶子节点只有两个子节点(即完全二叉树)
根节点高度为1,则高度为n的满二叉树所有节点树为2^n-1
2015个节点在高度10和11之间
2^10-1=1023
2^11-1=2047
完全二叉树最后一层都为叶子节点2015-1023=992个
倒数第2层有些没有子节点,也是叶子节点2047-2015=32,对应上一层会少一半32/2=16
所以总的叶子节点数量为992+16=1008
这篇关于信息学奥赛初赛天天练-80-NOIP2015普及组-基础题5-错位排列、二叉树、完全二叉树、叶子节点、完全二叉树叶子节点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








