LLM - GPT(Decoder Only) 类模型的 KV Cache 公式与原理 教程

本文主要是介绍LLM - GPT(Decoder Only) 类模型的 KV Cache 公式与原理 教程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

欢迎关注我的CSDN：https://spike.blog.csdn.net/
本文地址：https://spike.blog.csdn.net/article/details/141605718

免责声明：本文来源于个人知识与公开资料，仅用于学术交流，欢迎讨论，不支持转载。

---

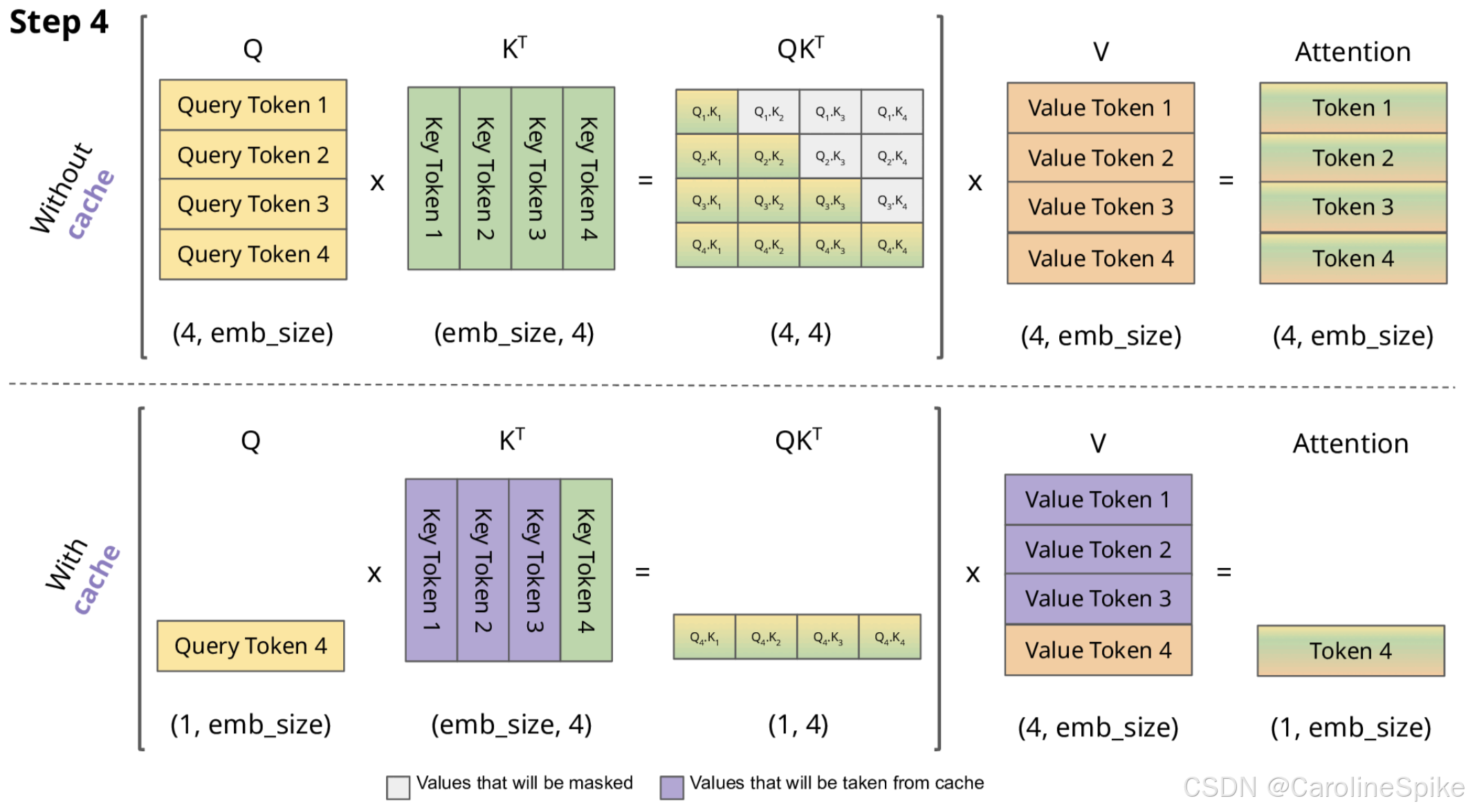
在 GPT 类模型中，KV Cache (键值缓存) 是用于优化推理效率的重要技术，基本思想是通过缓存先前计算的 键(Key) 和 值(Value)，避免在推理过程中，重复计算 Mask 的 注意力(Attention) 矩阵，从而加速生成过程。

1. 公式

矩阵乘法的基础性质：

$$A\cdot B=\left[\begin{array}{cccc}{A}_1& A_2& \dots & A_n\end{array}\right]\cdot \left[\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_n\end{array}\right]=A_1{B}_1+A_2{B}_2+\cdots +A_n{B}_n$$

其中 $A_i$ 是 $A$ 的列向量，$B_i$ 是 $B$ 的行向量，也就是说相同维度的向量相乘，可拆解成行向量乘以列向量，即 $A$ 有 $n$ 列，$B$ 有 $n$ 行。如图：

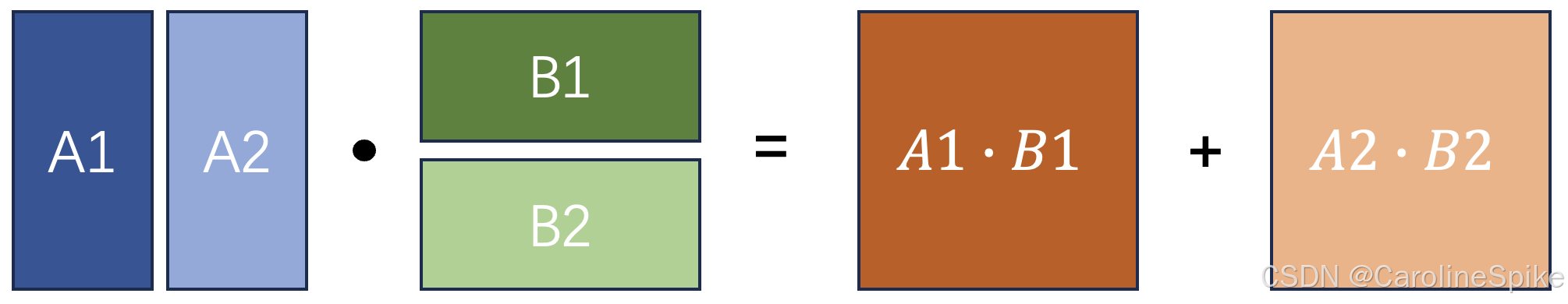
例如：基础的矩阵乘法：

$$\begin{gathered} A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right] \\ C=\left[\begin{array}{cc}1\ast 5+2\ast 7& 1\ast 6+2\ast 8\\ 3\ast 5+4\ast 7& 3\ast 6+4\ast 8\end{array}\right]=\left[\begin{array}{cc}19& 22\\ 43& 50\end{array}\right] \end{gathered}$$

也可以写成，行列向量相乘的形式，即 A 拆分出多个行向量，B 拆分出多个列向量，即：

$$C=\left[\begin{array}{c}1\\ 3\end{array}\right]\cdot \left[\begin{array}{cc}5& 6\end{array}\right]+\left[\begin{array}{c}2\\ 4\end{array}\right]\cdot \left[\begin{array}{cc}7& 8\end{array}\right]=\left[\begin{array}{cc}1\ast 5& 1\ast 6\\ 3\ast 5& 3\ast 6\end{array}\right]+\left[\begin{array}{cc}2\ast 7& 2\ast 8\\ 4\ast 7& 4\ast 8\end{array}\right]$$
$$=\left[\begin{array}{cc}1\ast 5+2\ast 7& 1\ast 6+2\ast 8\\ 3\ast 5+4\ast 7& 3\ast 6+4\ast 8\end{array}\right]=\left[\begin{array}{cc}19& 22\\ 43& 50\end{array}\right]$$

进一步拆解：

$$\begin{gathered} A\cdot B=A_1{B}_1+A_2{B}_2+\cdots +A_n{B}_n \\ =\left[\begin{array}{c}{a}_{1,1}{B}_1\\ a_{2,1}{B}_2\\ ⋮\\ a_{m,1}{B}_n\end{array}\right]+\left[\begin{array}{c}{a}_{1,2}{B}_1\\ a_{2,2}{B}_2\\ ⋮\\ a_{m,2}{B}_n\end{array}\right]+\cdots +\left[\begin{array}{c}{a}_{1,n}{B}_1\\ a_{2,n}{B}_2\\ ⋮\\ a_{m,n}{B}_n\end{array}\right] \\ =\left[\begin{array}{c}{a}_{1,1}{B}_1+a_{1,2}{B}_1+\cdots +a_{1,n}{B}_1\\ a_{2,1}{B}_2+a_{2,2}{B}_2+\cdots +a_{2,n}{B}_2\\ \cdots \\ a_{m,1}{B}_n+a_{m,2}{B}_n+\cdots +a_{m,n}{B}_n\end{array}\right] \end{gathered}$$

基础的矩阵乘法的另一种形式：

$$C=\left[\begin{array}{c}1\\ 3\end{array}\right]\cdot \left[\begin{array}{c}5,6\end{array}\right]+\left[\begin{array}{c}2\\ 4\end{array}\right]\cdot \left[\begin{array}{c}7,8\end{array}\right]$$
$$\left[\begin{array}{cc}1\ast [5& 6]\\ 3\ast [5& 6]\end{array}\right]+\left[\begin{array}{cc}2\ast [7& 8]\\ 4\ast [7& 8]\end{array}\right]$$
$$\left[\begin{array}{cc}1\ast 5& 1\ast 6\\ 3\ast 5& 3\ast 6\end{array}\right]+\left[\begin{array}{cc}2\ast 7& 2\ast 8\\ 4\ast 7& 4\ast 8\end{array}\right]=\left[\begin{array}{cc}19& 22\\ 43& 50\end{array}\right]$$

如果 $A$ 是下三角矩阵，即包含 Mask 信息，Decoder 无法观察到之后的推理部分，则 $A\cdot B$，输出：

$$A\cdot B=\left[\begin{array}{l}{a}_{1,1}{B}_1\\ a_{2,1}{B}_2+a_{2,2}{B}_2\\ \cdots \\ a_{m,1}{B}_n+a_{m,2}{B}_n+\cdots +a_{m,n}{B}_n\end{array}\right]$$

2. 推理

第1步：

在 Decoder 解码过程中，只关注 Transformer 的 自注意力(Self-Attention)，输入第 1 个 Token，将 Token 转换成 输入特征 $Inpu{t}_1=[1,d_{emb}]$，暂时忽略 batch_size，$d_{emb}$ 表示 Embedding Size。

1. 输入特征 $Inpu{t}_0=[1,d_{emb}]$，乘以权重 $W=[d_{emb},3\ast d_{emb}]$ (已训练完成，值是固定的)，输出维度 $[1,3\ast d_{emb}]$，即作为 Q\K\V，每个向量 $[1,d_{emb}]$。

   • $Q_1=[1,d_{emb}]$、$K_1=[1,d_{emb}]$、$V_1=[1,d_{emd}]$，只与输入特征 $Inpu{t}_0$ 的 Embedding 相关。

2. 根据 Self-Attention 的公式，忽略 $\sqrt{d}$，只有1维，mask 不起作用，即
   $$\begin{gathered} Att(Q,K,V)=softmax(Q{K}^{\top }+mask)\ast V \\ At{t}_1(Q,K,V)=softmax(Q_1{K}_1^{\top })V_1 \\ 其中softmax(x_i)=\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}} \end{gathered}$$

3. $At{t}_0$ ($[1,d_{emb}]$) 经过一系列推理，最后输出 $[1,d_v]$，$d_v$ 是全部词元 Token 的数量，根据概率值即可获得最后的 Token。

第 2 步：

将第 1 步输出的 Token 转换成 $[1,d_{emb}]$，与第 1 步组合至一起，即 输入特征 $Inpu{t}_1=[2,d_{emb}]$

1. 输入特征 $Inpu{t}_1=[2,d_{emb}]$，乘以权重 $W=[d_{emb},3\ast d_{emb}]$，权重是固定的，因此只需要计算第 2 个输入的特征 $[1,d_{emb}]$，第 1 个不需要计算，也就是说 Q\K\V 的维度是 $[2,d_{emb}]$，只需计算一次即可，剩余的可以直接 $concat$ 到一起。

2. 根据 Self-Attention 的公式，忽略 $\sqrt{d}$，注意第1行，已经计算，第2行，需要使用 $Q_2$、$K_2$、$V_2$，进行计算，即：
   $$\begin{gathered} At{t}_2(Q,K,V)=softmax(Q{K}^{\top }+mask)\ast V \\ softmax(\left[\begin{array}{l}{Q}_1{K}_1^{\top }\\ Q_2{K}_1^{\top }+Q_2{K}_2^{\top }\end{array}\right])\cdot \left[\begin{array}{c}{V}_1\\ V_2\end{array}\right] \\ =\left[\begin{array}{l}softmax(Q_1{K}_1^{\top })V_1\\ softmax(Q_2{K}_1^{\top })V_1+softmax(Q_2{K}_2^{\top })V_2\end{array}\right] \\ =\left[\begin{array}{c}At{t}_1(Q,K,V)\\ softmax(Q_2{K}_1^{\top })V_1+softmax(Q_2{K}_2^{\top })V_2\end{array}\right] \end{gathered}$$

3. KV 都是成对出现的，如果 缓存 KV，则可以加快推理速度。

第 3 步：重复进行。

3. 缓存占用

关于 Llama3 的 KV Cache 源码，参考 model.py：

xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)self.cache_k = self.cache_k.to(xq)
self.cache_v = self.cache_v.to(xq)self.cache_k[:bsz, start_pos : start_pos + seqlen] = xk
self.cache_v[:bsz, start_pos : start_pos + seqlen] = xvkeys = self.cache_k[:bsz, : start_pos + seqlen]
values = self.cache_v[:bsz, : start_pos + seqlen]

关于 KV 的缓存内存占用：

相关参数 batch_size=32，head=32，layer=32，dim_size=4096，seq_length=2048，float32(4个字节)类，计算 KV cache 的缓存占用：
$$\begin{gathered} M=2\ast N_{bs}\ast (N_{dim}/N_{head}\ast N_{head})\ast N_{layer}\ast N_{seq}\ast 4 \\ =2\ast 32\ast 4096\ast 32\ast 2048\ast 4/1024/1024/1024=64G \end{gathered}$$
也就是说 head 数量无关，因为维度除以 Head 再乘以 Head。Llama3 使用 GQA (Grouped Query Attention) 分组查询注意力机制，降低 4 倍的 KV Cache，head=32，kv_head=8，即 scale=head/kv_head=4。

参考：

• CSDN - 从头开始实现 LLaMA3 的网络结构与推理流程 教程
• Transformers KV Caching Explained

这篇关于LLM - GPT(Decoder Only) 类模型的 KV Cache 公式与原理 教程的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---