本文主要是介绍前端算法 === 力扣 111 二叉树的最小深度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
问题描述
DFS(深度优先搜索)方案
BFS(广度优先搜索)方案
总结
力扣(LeetCode)上的题目111是关于二叉树的最小深度问题。这个问题可以通过深度优先搜索(DFS)和广度优先搜索(BFS)两种方法来解决。下面我将分别对这两种方法进行讲解。
问题描述
给定一个二叉树,找出它的最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
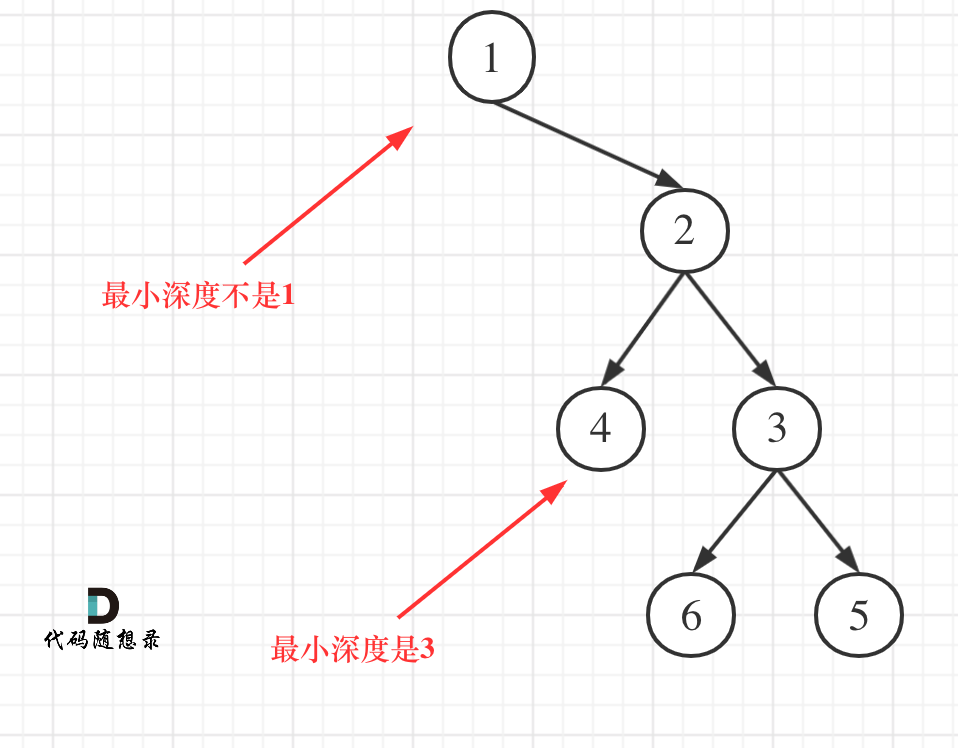
本题还有一个误区,题目中说的是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。,注意是叶子节点。
什么是叶子节点,左右都为空的节点才是叶子节点!
DFS(深度优先搜索)方案
DFS是一种自顶向下的搜索策略,它从根节点开始,尽可能深地搜索树的分支。在这个问题中,我们可以递归地遍历二叉树的每个节点,直到到达叶子节点。
- 基本情况:如果当前节点为空,返回0。
- 递归:分别对当前节点的左子树和右子树调用DFS,获取它们的最小深度。
- 比较:比较左子树和右子树的深度,取较小者加1(当前节点的深度)。
function minDepth(root) {// 基本情况:如果根节点为空,返回0,因为空树的深度是0if (root === null) {return 0;}// 如果左子树为空,只考虑右子树的深度if (root.left === null) {return minDepth(root.right) + 1; // 递归调用右子树,并将深度加1}// 如果右子树为空,只考虑左子树的深度if (root.right === null) {return minDepth(root.left) + 1; // 递归调用左子树,并将深度加1}// 如果左右子树都不为空,比较左右子树的深度,选择较小的深度,然后加1return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
}root:当前正在考虑的节点。root.left和root.right:当前节点的左子节点和右子节点。minDepth(root.left)和minDepth(root.right):递归调用函数本身,分别计算左子树和右子树的最小深度。Math.min(...):选择两个深度中的较小值。+1:因为我们在计算从根节点到叶子节点的路径长度,所以每经过一个节点,深度就加1。
递归的美妙之处在于它能够自然地处理树结构,每次递归调用都处理树的一个分支,直到达到叶子节点,然后逐层返回,直到得到整个树的最小深度。这种方法直观且易于理解,特别是对于树结构的问题。
BFS(广度优先搜索)方案
BFS是一种自底向上的搜索策略,它从根节点开始,逐层遍历树的所有节点。在这个问题中,我们可以使用队列来实现BFS。
- 初始化:创建一个队列,将根节点入队。
- 循环:只要队列不为空,执行以下操作:
- 取出队列中的所有节点,记为当前层。
- 对于当前层的每个节点,检查其左右子节点:
- 如果一个节点没有左子节点或右子节点,返回当前层的深度。
- 如果有子节点,将子节点加入队列。
- 层级计数:每处理完一层,深度计数器加1。
function minDepth(root) {if (!root) return 0;const queue = [[root, 1]];let depth = 1;while (queue.length) {const [node, d] = queue.shift();if (!node.left && !node.right) return d;if (node.left) queue.push([node.left, depth + 1]);if (node.right) queue.push([node.right, depth + 1]);}
}总结
DFS和BFS都是解决这个问题的有效方法。DFS的优点是代码简单,但可能在某些情况下效率不如BFS。BFS通常更直观,因为它逐层遍历树,而且对于这个问题,BFS可以更快地找到最小深度,因为它会在找到第一个叶子节点时立即停止搜索。然而,BFS需要额外的存储空间来存储队列。根据具体问题和场景,你可以选择适合的方法。
这篇关于前端算法 === 力扣 111 二叉树的最小深度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




