本文主要是介绍最大流的Ford-Fulkerson方法初步,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
网络或者网络流是一种基本的数据结构,而最大流则是网络流上的基本问题。网络本质上是一个符合一定条件的有向带权图。而最大流是最大可行流的简称,可行流是一个定义在网络流上的符合一定条件的函数。这些定义条件对于算法的正确性是不可缺少的,不过本文不描述可行流的数学条件,只介绍最大流最常用的Ford-Fulkerson方法的原理。
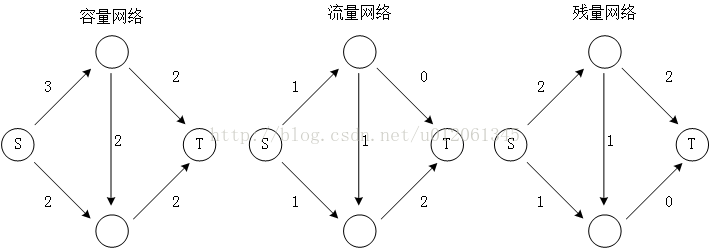
如上左的权图称作容量网络,边权值表示该边的容量。上中的权图称为流量网络,边权值表示该边经过的流量(这显然是一个可行流)。上右的图称为残量网络,边权值表示该边还能容纳多少流量。很显然,当可行流完全取0的时候,残量网络就是容量网络。
为了方便描述,给出增广路径的概念。增广路径就是残量网络上从源到汇的一条可行路径,可行就是边权值均为正。最大流算法的基本理论就是:最大流的充要条件是残量网络中不存在增广路径。因此,当可以在残量网络中找到一条增广路径时,就说明当前流不是最大流,同时也说明当前流至少可以加上增广路径的最小权值形成新的可行流。所以,最大流的基本算法就是在残量网络是寻找增广路径,然后累加即可;直到不存在增广路径即可。寻找增广路径可以使用搜索。

此时仍然有一个技术问题,关于反向边。考虑上图左的容量网络,假设第一次搜索到的增广路径如上中所示,则残量网络如上右所示。此时我们发现该残量网络已经不存在增广路径了,于是达到了最大流,答案为2。但很明显正确答案是4。此现象出现的原因是中间那条边。这个网络上要达到最大流就不能选用中间那条边,但是搜索时并不知道这一点。为了处理这个问题,加上反向边,初始时反向边容量均为0;反向边一样能够参与增广路径的搜索;搜索时,正向边每减去一个值,反向边就加上一个值。如下所示,与之前一模一样的搜索过程,得到了下右所示的残量网络。在这个网络上,经过中间的反向边仍然能搜索到增广路径。最后可以得到正确答案。所以,正向边、反向边各用一次,实际上就相当于没有选用。但使用反向边,就不必在搜索过程中回溯。技术上,反向边提供了“反悔”的机会。

明白增广路径与反向边后,理论上就能实现最大流了。最大流中经常说的FF方法就是指的基于此原理的方法。在此原理上,又有一些新的算法用于提高增广路径搜索的效率,但原理上仍然是基于FF方法的,包括EK、Dinic算法等。这些算法平衡性比较好,既能够满足绝大部分题目的需要,编码上也不过于复杂,因此FF类方法是最常用的最大流解法。hdu1532是一道基本的最大流,这里展示了FF方法的原理,使用了没有任何优化的增广路径搜索。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define SIZE 205typedef int weight_t;int N,M;//边的结构
struct edge_t{int node;weight_t c;//c为容量edge_t* next;edge_t* redge;//指向反向边bool isU;//正向边
}Edge[SIZE*2];
int ECnt;//图的邻接表
edge_t* Ver[SIZE];void init(){ECnt = 0;fill(Ver+1,Ver+M+1,(edge_t*)0);
}//生成双向边
void mkEdge(int a,int b,weight_t c){int t1 = ECnt++;int t2 = ECnt++;Edge[t1].node = b;Edge[t1].c = c;Edge[t1].next = Ver[a];Edge[t1].redge = Edge + t2;Edge[t1].isU = true;Ver[a] = Edge + t1;Edge[t2].node = a;Edge[t2].c = 0;Edge[t2].next = Ver[b];Edge[t2].redge = Edge + t1;Edge[t2].isU = false;Ver[b] = Edge + t2;
}bool read(){if ( EOF == scanf("%d%d",&N,&M) )return false;init();for(int i=0;i<N;++i){int a,b,c;scanf("%d%d%d",&a,&b,&c);mkEdge(a,b,c);}return true;
}
bool F[SIZE];
//u当前节点,f为当前流
int dfs(int u,int f){if ( u == M ) return f;F[u] = true;for(edge_t*p=Ver[u];p;p=p->next){int v = p->node;if( F[v] ) continue;weight_t c = p->c;if ( c > 0 ){int t = dfs(v,min(c,f));if ( 0 == t ) continue;p->c -= t;p->redge->c += t;return t;}}return 0;
}int solve(){int ret = 0;while(1){fill(F+1,F+M+1,false);int t = dfs(1,INT_MAX);if ( 0 == t ) return ret;ret += t;}
}int main(){while( read() )printf("%d\n",solve());return 0;
}
这篇关于最大流的Ford-Fulkerson方法初步的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!