本文主要是介绍算法设计与分析:分治法求最近点对问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、实验目的
1. 掌握分治法思想;
2. 学会最近点对问题求解方法。
二、实验内容
1. 对于平面上给定的N个点,给出所有点对的最短距离,即,输入是平面上的N个点,输出是N点中具有最短距离的两点。
2. 要求随机生成N个点的平面坐标,应用蛮力法编程计算出所有点对的最短距离。
3. 要求随机生成N个点的平面坐标,应用分治法编程计算出所有点对的最短距离。
4. 分别对N=100000~1000000,统计算法运行时间,比较理论效率与实测效率的差异,同时对蛮力法和分治法的算法效率进行分析和比较。
5. 如果能将算法执行过程利用图形界面输出,可获加分。
三、算法思想
1. 预处理:根据输入点集S中的x轴和y轴坐标进行排序,得到X和Y,很显然此时X和Y中的点就是S中的点。
2. 点数较少时的情形
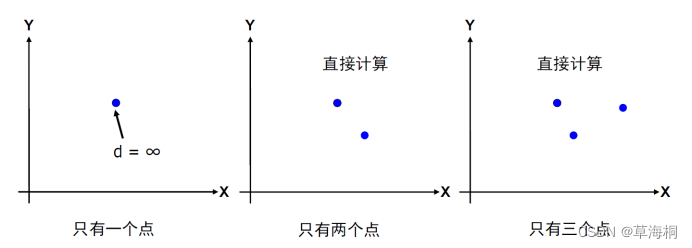
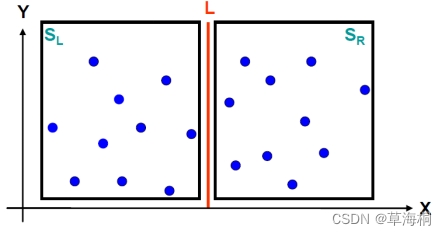
3. 点数|S|>3时,将平面点集S分割成为大小大致相等的两个子集SL和SR,选取一个垂直线L作为分割直线,如何以最快的方法尽可能均匀平分?注意这个操作如果达到效率O(n^2),将导致整个算法效率达O(n^2)。
4. 两个递归调用,分别求出SL和SR中的最短距离为dl和dr。
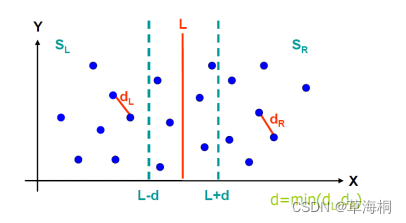
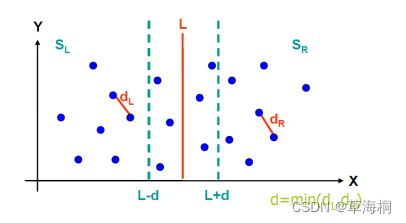
5. 取d=min(dl, dr),在直线L两边分别扩展d,得到边界区域Y,Y'是区域Y中的点按照y坐标值排序后得到的点集(为什么要排序?),Y'又可分为左右两个集合Y'L和Y'R
6. 对于Y'L中的每一点,检查Y'R中的点与它的距离,更新所获得的最近距离,注意这个步骤的算法效率,请务必做到线性效率,并在实验报告中详细解释为什么能做到线性效率?

四、实验步骤
先定义全局变量和点结构:
#define max 10000000000;//假定最大距离
int n,m,**v;
//n为规模,m为创建点集合过程时的点数,v用于判断是否已有该点(rand不产生大于40000的数)
double time1,time2;//蛮力法、分治法花费的时间
double dt1,dt2;//蛮力法、分治法求得的最近距离
//---------------------------
struct D{//点结构int x=0,y=0;
};
D a1,b1,a2,b2;//a1、b1为蛮力法求得的点的下标,a2、b2为分治法求得的点的下标
D *k,*p;//蛮力法、分治法用的点集合1、蛮力法
对前面n-1个点的每一个点,均与在其后面的每个点进行距离计算,并与最小距离min比较,若比min小,则更新min的值,时间复杂度为O(n2)。
伪代码:
Manli(A)min=Infinity//最小距离for i=0 to A.length-1for j=i+1 to A.lengthd=dis(A[i],A[j])//A[i]、A[j]两点的距离if d<minmin=da=ib=ja1=ab1=breturn min2、分治法
2.1 先用快速排序SortX(A,1,n)将所有点按x坐标升序排序
方便分治均匀,时间复杂度为O(nlgn)。
SortX(l,r)i=l,j=r,keyx=A[l].x,keyy=A[l].y //Array A is a global variablewhile i<jwhile i<j and A[j].x>=keyxj--if i<jA[i]=A[j]i++elsebreakwhile i<j and A[i].x<=keyxi++if i<jA[j]=A[i]j--A[i].x=keyx,A[i].y=keyyif(l<i-1) SortX(l,i-1)if(i+1<r) SortX(i+1,r)2.2 点数n<=3时直接计算,时间复杂度为O(1)
2.3 点数n>3时
将平面点集S分割成为大小大致相等的两个子集SL和SR,选取一个垂直线L(以x坐标居中的为分治点,上面已排序好了)作为分割直线。
两个子集递归调用(当只有一个元素时返回无穷大,两个时按y升序排序这两个元素),分别求出SL和SR中的最短距离dl和dr。
取最小值d=min(dl, dr),在直线L两边分别扩展d,得到边界区域Y。
然后用Marge(l,mid,r)函数按纵坐标升序归并左右两部分点集合,时间复杂度O(n)
由于前面点已按y升序排序,所以在区域Y中,两点距离小于当前min的可能情况为在一个长2*d,、宽d的长方形内。
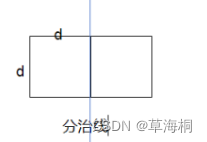
由于已知两边的最小距离为d,则对在这个长方形内任意一点P,距P为d的点Q的个数不超过6个,例如下面的点P最多在左右两个正方形的6条边上各有一个点距P为d(但是此情况下,在同一个正方形内的其他两个点的距离已经小于当前最小距离小于d了,所以可能的点数不超过6);
再或者是说,在这个长方形内,最多就六个点相距d,即六个顶点。
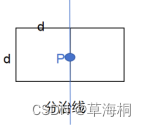
所以,只需要对t点集中的每个点与其后面的5个点比较距离是否小于当前最小距离d并更新d就行。时间复杂度O(n)。
综上所述,T(n)=2*T(n/2)+f(n)。f(n)为Marge和遍历t点集,时间复杂度均为O(n),共递归lgn次,则时间复杂度为O(nlgn)。前面按x坐标排序的时间复杂度为O(nlgn),所以总的时间复杂度为O(nlgn)。
伪代码如下:
Fenzhi(l,r)if l==r //一个点return max //直接返回无穷大if l+1==r //两个点,按y升序排序a2=A[l]b2=A[r]A[l]=a2.y<b2.y?a2:b2 //y坐标较小的点A[r]=a2.y>b2.y?a2:b2 //y坐标较大的点return dis(A[l],A[r])if l+1<r //点数大于2mid=(r+l)/2 mid为分治中点,将点集合划分为左右均匀的两部分d=min(Fenzhi(l,mid),Fenzhi(mid+1,r))//d取左右两部分最小距离的较小值Merge(l,mid,r) //按纵坐标升序归并左右两部分的点*t=new Point[r-l+1]//记录跨中线且距离分治中点d水平距离小于当前最小值d的异侧点tn=0 //t点集的元素个数for i=1 to rif A[i].x>(A[i].x-d) and A[i].x<(A[i].x+d)//异侧且距分治中心mid小于d则入tt[tn++]=A[i]for i=0 to tn-1for j=i+1 to tn-1 and j<i+6 //往后判断5个点//t[]中y升序,若y坐标差已超过当前d,break,判断下一个点if t[j].y-t[i].y>dbreakif dis(t[i],t[j])<d //如果当前点距离小于等于当前d,则对最小距离d进行更新d=dis(t[i],t[j])a2=t[i]b2=t[j]return d //返回当前分治的最小距离运行结果如下(取其中两例):两种方法求得的最近距离一致(虽然不一定是同一对点),且分治法更快。可见算法查找正确。

五、实验结果和分析
分别对N=100000~1000000,统计算法运行时间,比较理论效率与实测效率的差异,同时对蛮力法和分治法的算法效率进行分析和比较。
这里修改了代码,对每个规模N均运行5趟取平均时间。
| 算法 | 规模N: | 5000 | 10000 | 20000 | 30000 | 50000 | 70000 | 100000 |
| 蛮力法 | 实测效率/s | 0.334 | 1.2372 | 4.7186 | 10.0754 | 30.1722 | 59.1302 | 120.953 |
| 理论效率/s | 0.3076 | 1.2304 | 4.9216 | 11.0736 | 30.76 | 60.2896 | 123.04 | |
| 表1 | ||||||||
| 算法 | 规模N: | 50000 | 100000 | 200000 | 300000 | 500000 | 700000 | 1000000 |
| 分治法 | 实测效率/s | 0.058 | 0.156 | 0.266 | 0.3618 | 0.726 | 1.012 | 1.44 |
| 理论效率/s | 0.0601 | 0.1278 | 0.271 | 0.42 | 0.7283 | 1.0458 | 1.5336 | |
对于蛮力法,
T实测=k·n2实测
T理论=k·n2理论
所以可得
T理论=T实测·(n理论/n实测)2
根据上式,以N=10000为基准,求出蛮力法的理论效率。
对于分治法
T实测=k·n实测lgn实测
T理论=k·n理论lgn理论
所以可得
T理论=T实测·(n理论·lgn理论)/(n实测·lgn实测)
根据上式,以N=100000为基准,求出分治法的理论效率。
作出蛮力法的实测效率和理论效率曲线图如下:
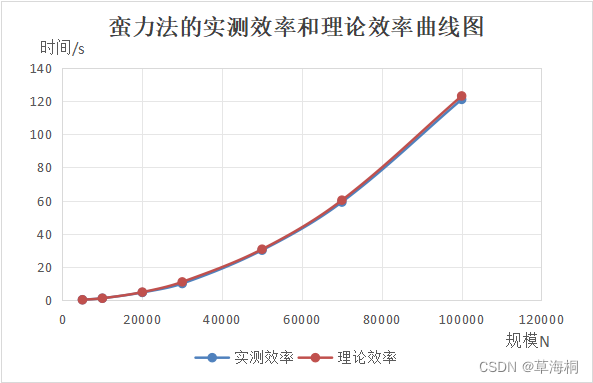
可以看出,实测效率和理论效率曲线贴合度很高,也都符合n2二次曲线。n=100000时的时间消耗,基本约为n=10000时的100倍。
作出分治法的实测效率和理论效率的曲线图如下:
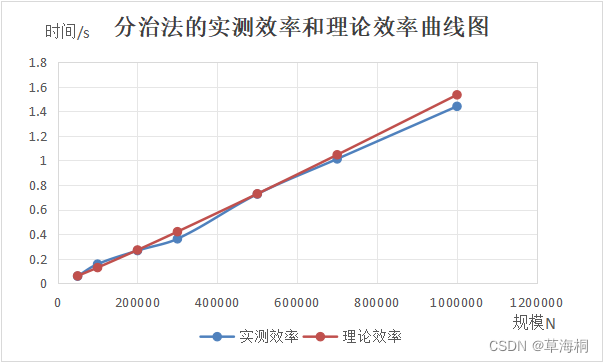
可以看出,分治法的实测曲线和理论曲线贴合度还行,但没有蛮力法的两条贴合度高,可能是由于实验次数不够大(只进行5次取平均)。符合nlgn型曲线走势。
对比两种方法,分治法效率明显由于蛮力法,尤其是当规模N持续增大时。
这篇关于算法设计与分析:分治法求最近点对问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







