代码随想录算法训练营第十六天| 找树左下角的值、路径总和、 从中序与后序遍历序列构造二叉树

本文主要是介绍代码随想录算法训练营第十六天| 找树左下角的值、路径总和、 从中序与后序遍历序列构造二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

找树左下角的值

题目链接：找树左下角的值
文档讲解：代码随想录
状态：递归没想到中右左的遍历顺序，迭代想出来了

思路：需要找最大深度，然后使用中右左的遍历顺序找最左节点
题解：

    int res = 0;int maxDepth = 0;public int findBottomLeftValue(TreeNode root) {dfs(root, 0);return res;}//中右左public void dfs(TreeNode root, int depth) {if (root == null) {return;}depth++;dfs(root.left, depth);dfs(root.right, depth);if (depth > maxDepth) {maxDepth = depth;res = root.val;}}

递归题解：层次遍历最后一行第一个数即可

   public int findBottomLeftValue(TreeNode root) {if (root == null) {return 0;}Deque<TreeNode> deque = new LinkedList<>();deque.addLast(root);int ans = root.val;while (!deque.isEmpty()) {int size = deque.size();TreeNode node = deque.peekFirst();ans = node.val;while (size-- > 0) {deque.pollFirst();while (node.left != null) {deque.addLast(node.left);}while (node.right != null) {deque.addLast(node.right);}}}return ans;}

路径总和

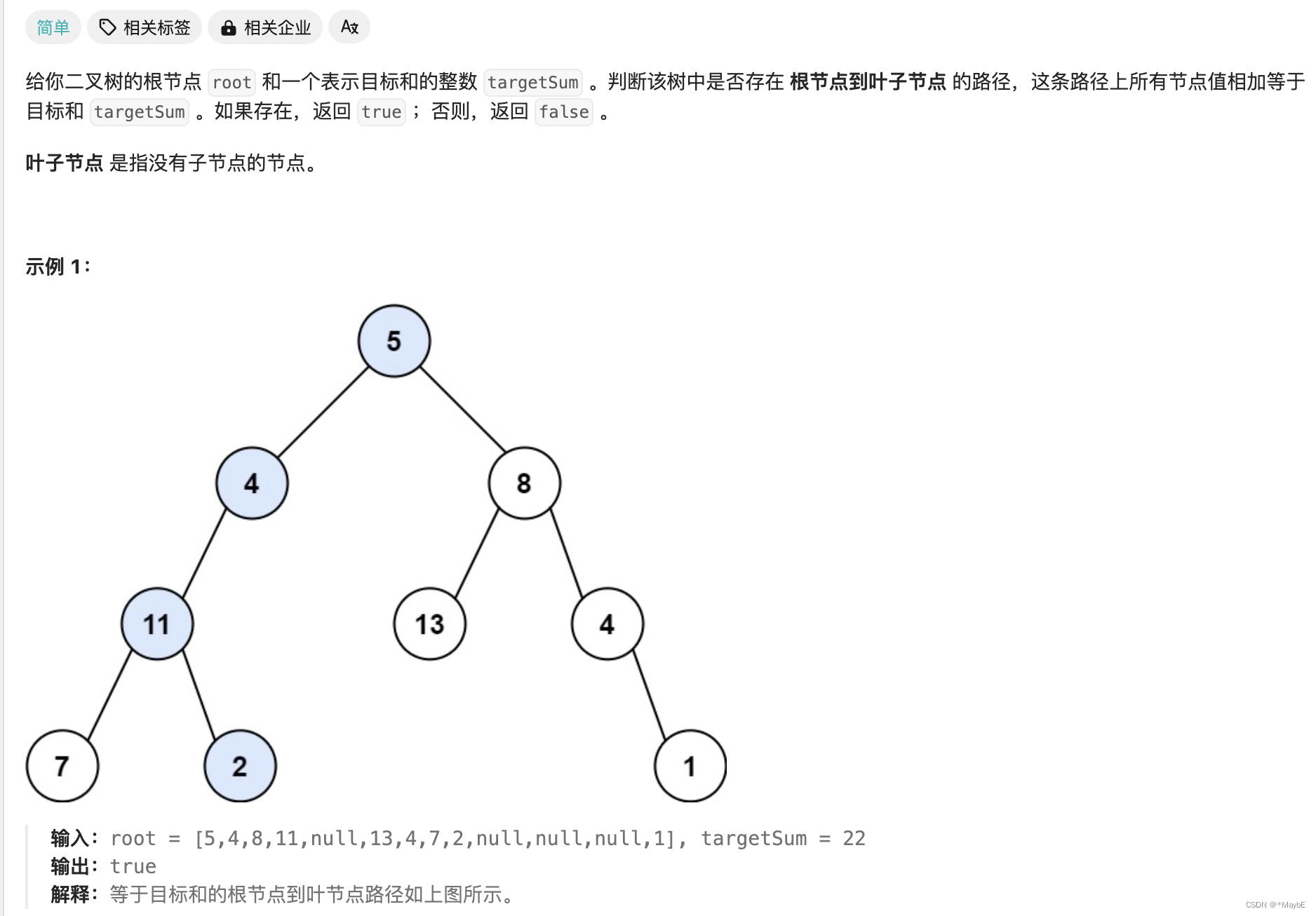
题目链接：路径总和
文档讲解：代码随想录
状态：还行

思路：看到有返回值，说明可以考虑左右子树进行相同的递归操作，即分别判断它们的子树是否满足条件。
递归题解：

public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) {return false;}// 如果当前节点是叶子节点，并且从根节点到该节点的路径和等于目标和，则返回true// 这里的条件是：当前节点的值等于剩余的目标和，且没有左右子节点if (targetSum - root.val == 0 && root.left == null && root.right == null) {return true;}// 递归地检查当前节点的左子树和右子树，看是否存在符合条件的路径// 如果左子树或右子树中存在符合条件的路径，则返回true// 否则，返回falsereturn hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}

从中序与后序遍历序列构造二叉树

题目链接：从中序与后序遍历序列构造二叉树
文档讲解：代码随想录
状态：没做出来，主要是使用案例中的数组去构建数的时候，误以为inorder中第一个数就是左节点了

思路： 如何根据两个顺序构造一个唯一二叉树?

• 以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。
• 一层一层切下去，每次后序数组最后一个元素就是节点元素。

例如:inorder = [9,3,15,20,7] 中序:左中右, postorder = [9,15,7,20,3] 后序:左右中

• 先看后序中的3肯定是中间结点,然后3在中序中分割,9肯定是左子树,15,20,7肯定属于右子树,
• 再回到后序,中序中的9是左子树结点,所以在后序中,9是左,15,7,20属于右子树
• 15,7,20中,20肯定是中间结点,所以回到中序中的15,20,7 肯定15属于左子树,7属于右子树

那么代码应该怎么写呢？

• 第一步：如果数组大小为零的话，说明是空节点了。
• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
• 第五步：切割后序数组，切成后序左数组和后序右数组
• 第六步：递归处理左区间和右区间
• 注意:要统一分割区间时,是左闭右开还是左闭右闭!!!

题解：

    Map<Integer, Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map = new HashMap<>();// 用map保存中序序列的数值对应位置for (int i = 0; i < inorder.length; i++) {map.put(inorder[i], i);}//前闭后开return findNode(inorder, 0, inorder.length, postorder, 0, postorder.length);}public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {//参数里面的范围都是前闭后开if (inBegin >= inEnd || postBegin >= postEnd) {// 不满足左闭右开，说明没有元素，返回空树return null;}//找到后序遍历中的最后一个元素int rootIndex = map.get(postorder[postEnd - 1]);//例如,找到后序中的3在中序中的位置为1//构造结点TreeNode root = new TreeNode(inorder[rootIndex]);// 保存中序左子树个数，用来确定后序数列的个数int lenOfLeft = rootIndex - inBegin;//例如,1-0 = 1// inorder:[9] postorder:[9]root.left = findNode(inorder, inBegin, rootIndex, postorder, postBegin, postBegin + lenOfLeft);// inorder:[15,20,7] postorder:[15,7,20]root.right = findNode(inorder, rootIndex + 1, inEnd, postorder, postBegin + lenOfLeft, postEnd - 1);return root;}

这篇关于代码随想录算法训练营第十六天| 找树左下角的值、路径总和、 从中序与后序遍历序列构造二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---