本文主要是介绍群体优化算法----人工蜂群优化算法应用于路径规划(机器人避开平面障碍寻找最短路线),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
介绍
人工蜂群优化算法(Artificial Bee Colony Algorithm, ABC)是由Dervis Karaboga在2005年提出的一种模拟蜜蜂觅食行为的优化算法。该算法基于蜜蜂群体的分工合作和信息交流机制,通过模拟蜜蜂寻找食物源的过程来解决优化问题。ABC算法因其简单、灵活和有效的特点,被广泛应用于各类优化问题,如函数优化、数据挖掘、路径规划等
概念
ABC算法主要模拟了三类蜜蜂的行为:雇佣蜂、观察蜂和侦查蜂。
雇佣蜂(Employed Bees):负责在食物源附近进行局部搜索,并将食物源的信息传递给观察蜂。
观察蜂(Onlooker Bees):在蜂巢中通过观察雇佣蜂的舞蹈选择食物源进行进一步搜索。
侦查蜂(Scout Bees):负责在全局范围内随机搜索新的食物源,以替代那些被淘汰的食物源。
步骤
初始化:在搜索空间内随机生成若干个食物源(即解),并计算其适应度值。
雇佣蜂阶段:
每只雇佣蜂在其对应的食物源附近随机选择一个新的解。
计算新解的适应度值,如果新解优于当前解,则更新当前解。
观察蜂阶段:
观察蜂根据雇佣蜂的舞蹈(适应度值)选择食物源,进行局部搜索。
与雇佣蜂阶段类似,计算新解的适应度值并进行更新。
侦查蜂阶段:
对于那些长时间未被改进的食物源,由侦查蜂进行全局随机搜索,以寻找新的潜在食物源。
终止条件:重复上述步骤直到满足终止条件(如达到最大迭代次数或满足精度要求)。
本文示例
模拟了机器人在一个二维平面内的路径规划问题,目标是找到一条最优路径,使得机器人能够从起点移动到终点,避开障碍物
路径规划问题定义
假设一个二维平面中有若干障碍物,机器人需要从起点(Start)移动到终点(Goal),避开所有障碍物,找到一条最短路径
代码
clc;
clear;% 参数设置
numBees = 50; % 蜂群规模(食物源数量)
maxIter = 1000; % 最大迭代次数
limit = 100; % 限制参数,用于判断是否需要启用侦查蜂
dim = 2; % 问题维度
numObstacles = 10; % 障碍物数量
mapSize = [100, 100]; % 地图大小% 起点和终点位置
startPoint = [10, 10];
endPoint = [90, 90];% 障碍物位置
obstacles = rand(numObstacles, 2) .* repmat(mapSize, numObstacles, 1);% 初始化食物源
foodSources = rand(numBees, dim) .* repmat(mapSize, numBees, 1);
fitness = calculateFitness(foodSources, startPoint, endPoint, obstacles, mapSize);
trials = zeros(numBees, 1);% 绘制地图
figure;
hold on;
axis([0 mapSize(1) 0 mapSize(2)]);
plot(startPoint(1), startPoint(2), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');
plot(endPoint(1), endPoint(2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
for i = 1:numObstaclesplot(obstacles(i, 1), obstacles(i, 2), 'ks', 'MarkerSize', 10, 'MarkerFaceColor', 'k');
end% 主循环
for iter = 1:maxIter% 雇佣蜂阶段for i = 1:numBeesk = randi([1, dim]);phi = rand * 2 - 1;newSolution = foodSources(i, :);newSolution(k) = foodSources(i, k) + phi * (foodSources(i, k) - foodSources(randi([1, numBees]), k));newFitness = calculateFitness(newSolution, startPoint, endPoint, obstacles, mapSize);if newFitness < fitness(i)foodSources(i, :) = newSolution;fitness(i) = newFitness;trials(i) = 0;elsetrials(i) = trials(i) + 1;endend% 观察蜂阶段prob = fitness / sum(fitness);for i = 1:numBeesif rand < prob(i)k = randi([1, dim]);phi = rand * 2 - 1;newSolution = foodSources(i, :);newSolution(k) = foodSources(i, k) + phi * (foodSources(i, k) - foodSources(randi([1, numBees]), k));newFitness = calculateFitness(newSolution, startPoint, endPoint, obstacles, mapSize);if newFitness < fitness(i)foodSources(i, :) = newSolution;fitness(i) = newFitness;trials(i) = 0;elsetrials(i) = trials(i) + 1;endendend% 侦查蜂阶段for i = 1:numBeesif trials(i) > limitfoodSources(i, :) = rand(1, dim) .* mapSize;fitness(i) = calculateFitness(foodSources(i, :), startPoint, endPoint, obstacles, mapSize);trials(i) = 0;endend% 绘制当前最优路径[bestFitness, bestIndex] = min(fitness);bestSolution = foodSources(bestIndex, :);plotPath(startPoint, bestSolution, endPoint, obstacles);drawnow;
end% 计算适应度函数
function fitness = calculateFitness(solutions, startPoint, endPoint, obstacles, mapSize)numSolutions = size(solutions, 1);fitness = zeros(numSolutions, 1);for j = 1:numSolutionssolution = solutions(j, :);path = [startPoint; solution; endPoint];pathLength = 0;for i = 1:(size(path, 1) - 1)pathLength = pathLength + norm(path(i, :) - path(i + 1, :));endfor i = 1:size(obstacles, 1)if min(sqrt(sum((path - obstacles(i, :)).^2, 2))) < 5pathLength = pathLength + 10000; % 惩罚因子endendfitness(j) = pathLength;end
end% 绘制路径
function plotPath(startPoint, solution, endPoint, obstacles)path = [startPoint; solution; endPoint];plot(path(:, 1), path(:, 2), 'b-o');plot(startPoint(1), startPoint(2), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g');plot(endPoint(1), endPoint(2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');for i = 1:size(obstacles, 1)plot(obstacles(i, 1), obstacles(i, 2), 'ks', 'MarkerSize', 10, 'MarkerFaceColor', 'k');end
end效果
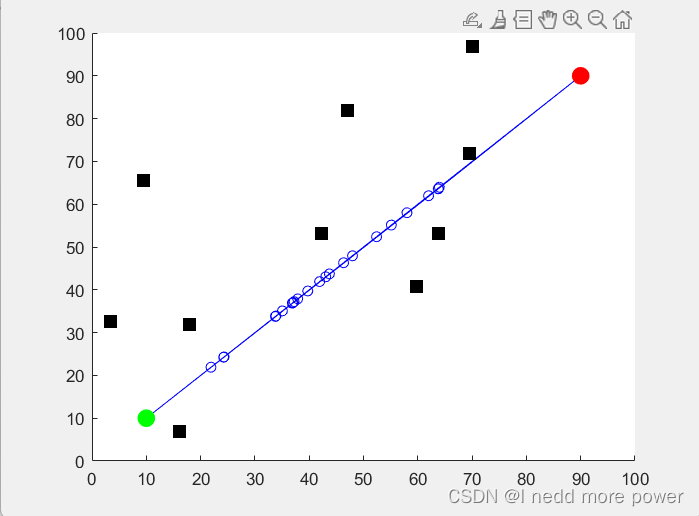
说明
初始化部分:
设置蜂群规模、最大迭代次数等参数。
定义地图大小、起点和终点的位置,以及障碍物的位置。
初始化食物源(即路径中的中间点)和计算初始适应度。
主循环部分:
雇佣蜂阶段:雇佣蜂在当前食物源附近进行局部搜索,并根据适应度值决定是否更新食物源。
观察蜂阶段:观察蜂根据雇佣蜂的舞蹈(适应度值)选择食物源进行进一步搜索。
侦查蜂阶段:对长时间未被改进的食物源进行全局随机搜索,以寻找新的潜在食物源。
实时绘制当前最优路径,以便观察算法的收敛过程。
适应度函数:
计算路径的总长度作为适应度值,同时对路径经过障碍物的情况进行惩罚,以避免路径穿越障碍物。
路径绘制:
绘制当前最优路径、起点、终点和障碍物,以便观察路径规划的效果
这篇关于群体优化算法----人工蜂群优化算法应用于路径规划(机器人避开平面障碍寻找最短路线)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




