本文主要是介绍【强化学习】DPO(Direct Preference Optimization)算法学习笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【强化学习】DPO(Direct Preference Optimization)算法学习笔记
- RLHF与DPO的关系
- KL散度
- Bradley-Terry模型
- DPO算法流程
- 参考文献
RLHF与DPO的关系
- DPO(Direct Preference Optimization)和RLHF(Reinforcement Learning from Human Feedback)都是用于训练和优化人工智能模型的方法,特别是在大型语言模型的训练中
- DPO和RLHF都旨在通过人类的反馈来优化模型的表现,它们都试图让模型学习到更符合人类偏好的行为或输出
- RLHF通常涉及三个阶段:全监督微调(Supervised Fine-Tuning)、奖励模型(Reward Model)的训练,以及强化学习(Reinforcement Learning)的微调
- DPO是一种直接优化模型偏好的方法,不需要显式地定义奖励函数,而是通过比较不同模型输出的结果,选择更符合人类偏好的结果作为训练目标,主要是通过直接最小化或最大化目标函数来实现优化,利用偏好直接指导优化过程,而不依赖于强化学习框架

KL散度
- KL散度(Kullback-Leibler divergence),也被称为相对熵,是衡量两个概率分布P和Q差异的一种方法
- 公式: K L ( P ∣ ∣ Q ) = ∑ x P ( x ) log ( P ( x ) Q ( x ) ) \mathrm{KL}(P||Q)=\sum_xP(x)\log\left(\frac{P(x)}{Q(x)}\right) KL(P∣∣Q)=∑xP(x)log(Q(x)P(x))
- KL散度是不对称的, K L ( P ∣ ∣ Q ) ! = K L ( Q ∣ ∣ P ) KL(P||Q)!=KL(Q||P) KL(P∣∣Q)!=KL(Q∣∣P)

Bradley-Terry模型
-
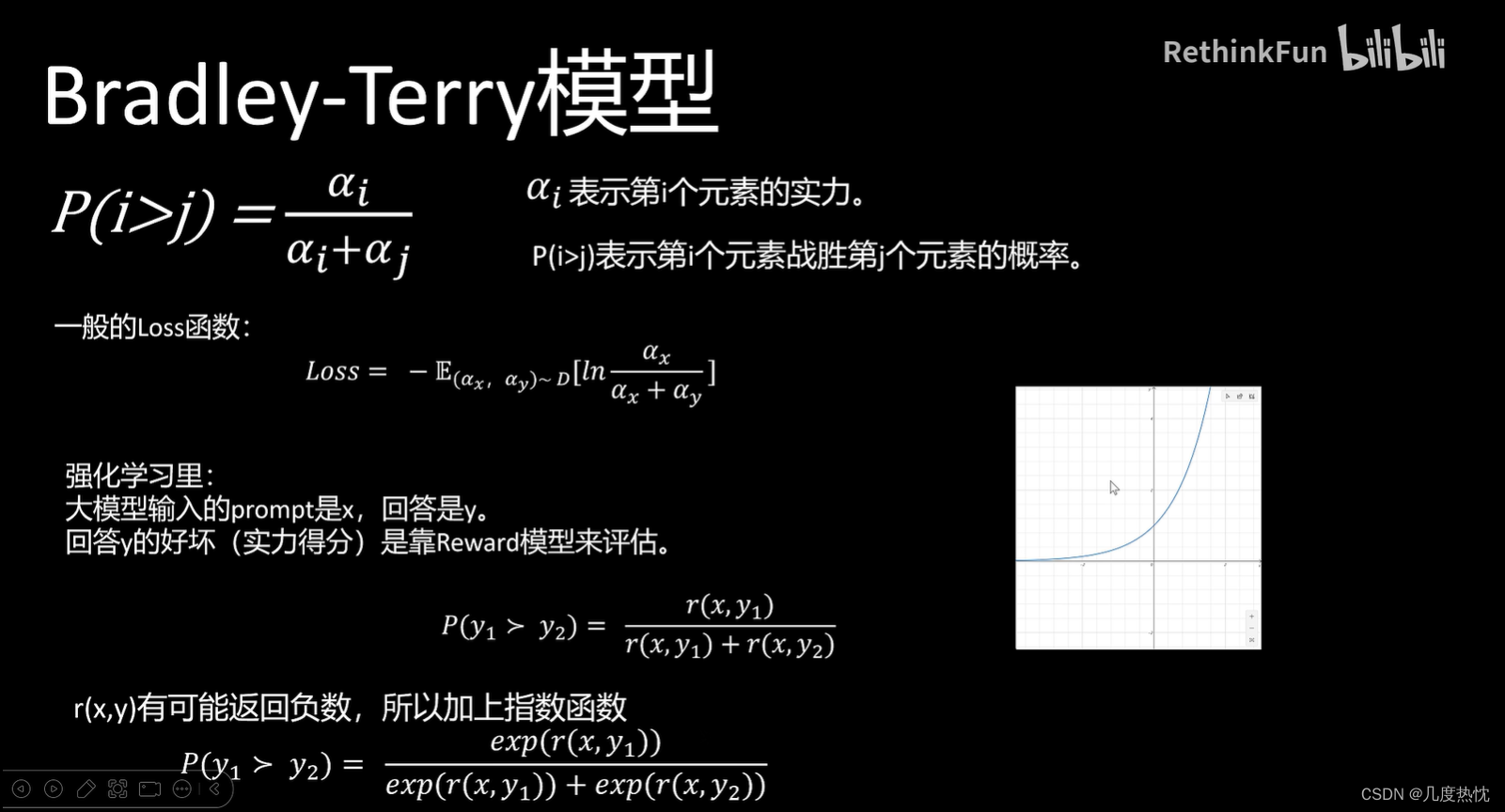
Bradley-Terry模型是一种用于比较成对对象并确定相对偏好或能力的方法。这种模型特别适用于对成对比较数据进行分析,从而对一组对象进行排序
-
P ( i > j ) = α i α i + α j P(i{>}j)=\frac{\alpha_i}{\alpha_i{+}\alpha_j} P(i>j)=αi+αjαi
-
α i \alpha_i αi表示第 i i i个元素的能力参数,且大于0。 P ( i > j ) P(i>j) P(i>j)表示第 i i i个元素战胜第 j j j个元素的概率
-
Bradley-Terry模型的参数通常通过最大似然估计(MLE)来确定
-
sigmoid函数: σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
-
loss函数的化简
L o s s = − E ( x , y w , y l ) ∼ D [ ln e x p ( r ( x , y w ) ) e x p ( r ( x , y w ) ) + e x p ( r ( x , y l ) ) ] = − E ( x , y w , y l ) ∼ D [ ln 1 1 + e x p ( r ( x , y l ) − r ( x , y w ) ) ] = − E ( x , y w , y l ) ∼ D [ ln σ ( r ( x , y w ) − r ( x , y l ) ) ] \begin{aligned}Loss &=-\mathbb{E}_{(x,y_{w},y_{l})\sim D}[\ln\frac{exp(r(x,y_{w}))}{exp(r(x,y_{w}))+exp(r(x,y_{l}))}] \\ &= -\mathbb{E}_{(x,y_{w},y_{l})\sim D}[\ln\frac{1}{1 + exp(r(x,y_{l})- r(x,y_{w}))}] \\ &= -\mathbb{E}_{(x,y_{w},y_{l})\sim D}[\ln \sigma(r(x,y_{w})-r(x,y_{l}))] \end{aligned} Loss=−E(x,yw,yl)∼D[lnexp(r(x,yw))+exp(r(x,yl))exp(r(x,yw))]=−E(x,yw,yl)∼D[ln1+exp(r(x,yl)−r(x,yw))1]=−E(x,yw,yl)∼D[lnσ(r(x,yw)−r(x,yl))] -
loss函数的目标是优化LLM输出的 y w y_w yw,经过reward计算的得分尽可能的大于 y w y_w yw经过reward计算的得分

DPO算法流程
- DPO通过比较不同输出的偏好,构建一个目标函数,该函数直接反映人类的偏好,通常使用排序损失函数(例如Pairwise Ranking Loss),该函数用来衡量模型在用户偏好上的表现
- DPO优化过程:使用梯度下降等优化算法,直接最小化或最大化目标函数。通过不断调整模型参数,使得模型生成的输出更加符合用户的偏好

- 基准模型一般指经过SFT有监督微调后的模型
- DPO的目标是尽可能得到多的奖励,同时使得新训练的 模型尽可能与基准模型分布一致
DPO训练目标的化简
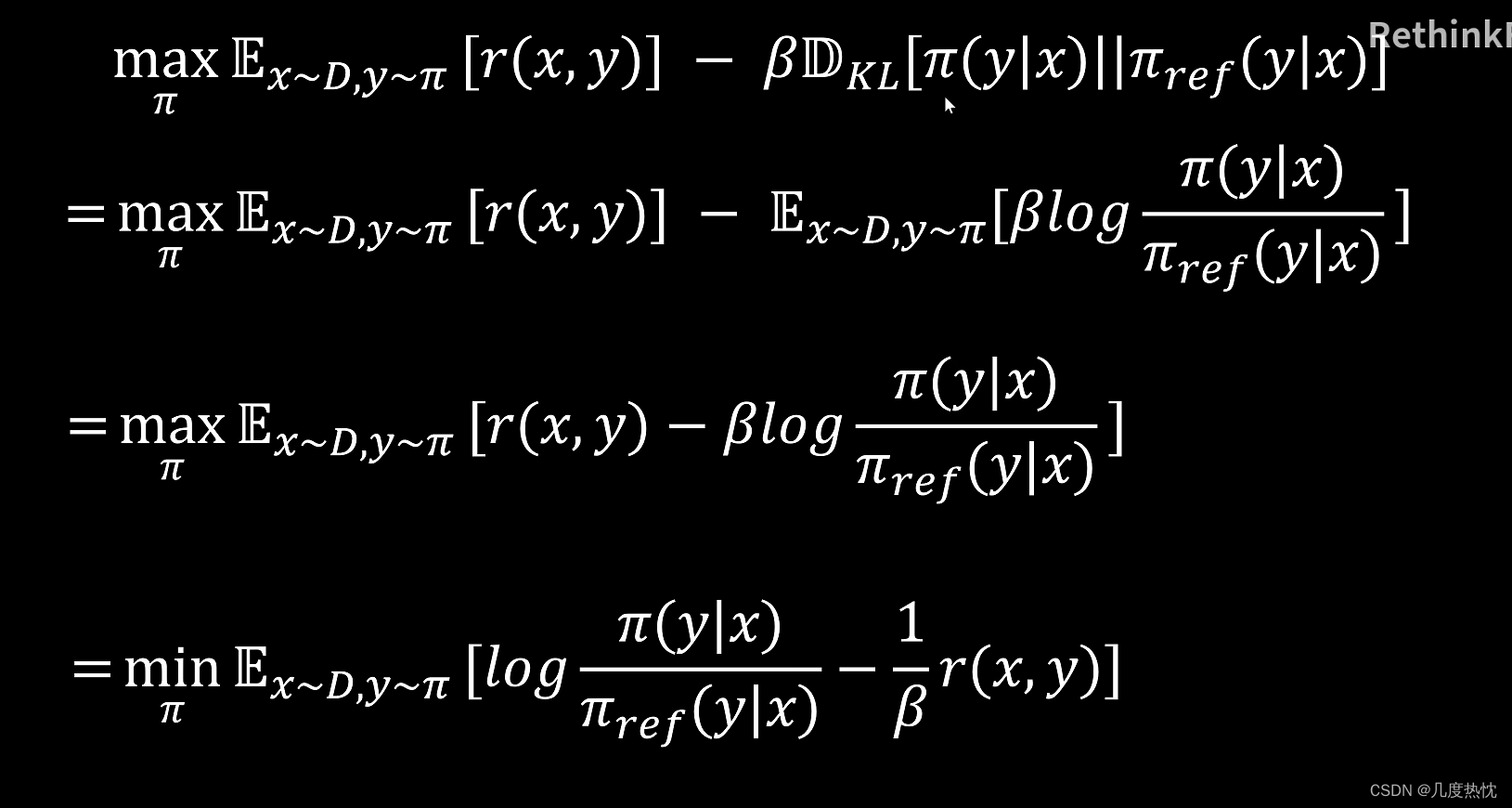
上图中第一步利用的是KL散度的定义,之所以式子中没有KL散度中的 P ( π ( y ∣ x ) ) P(\pi(y|x)) P(π(y∣x)),是因为KL散度可以理解成是一个概率比值的log的期望,在这里这个概率以期望的形式放到式子左边的期望中了
- 求最大值 通过在式中加上负号转化为求最小值,并同时除以 β \beta β
- DPO原论文中的推导过程

- 继续推导

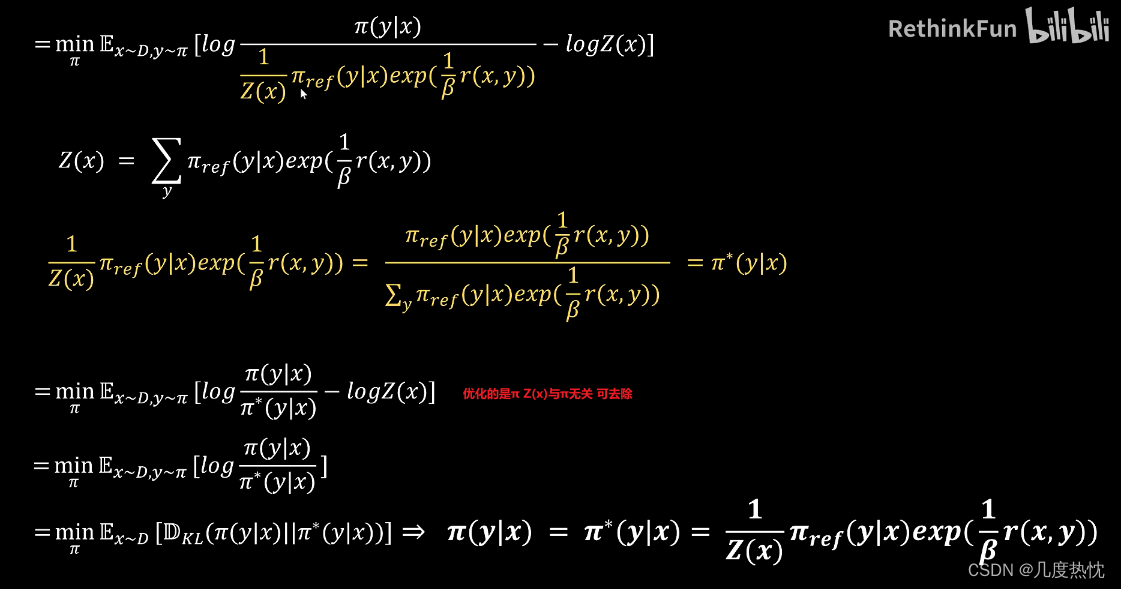
- 求解reward函数的表达式,将reward函数的表达式代入loss函数中
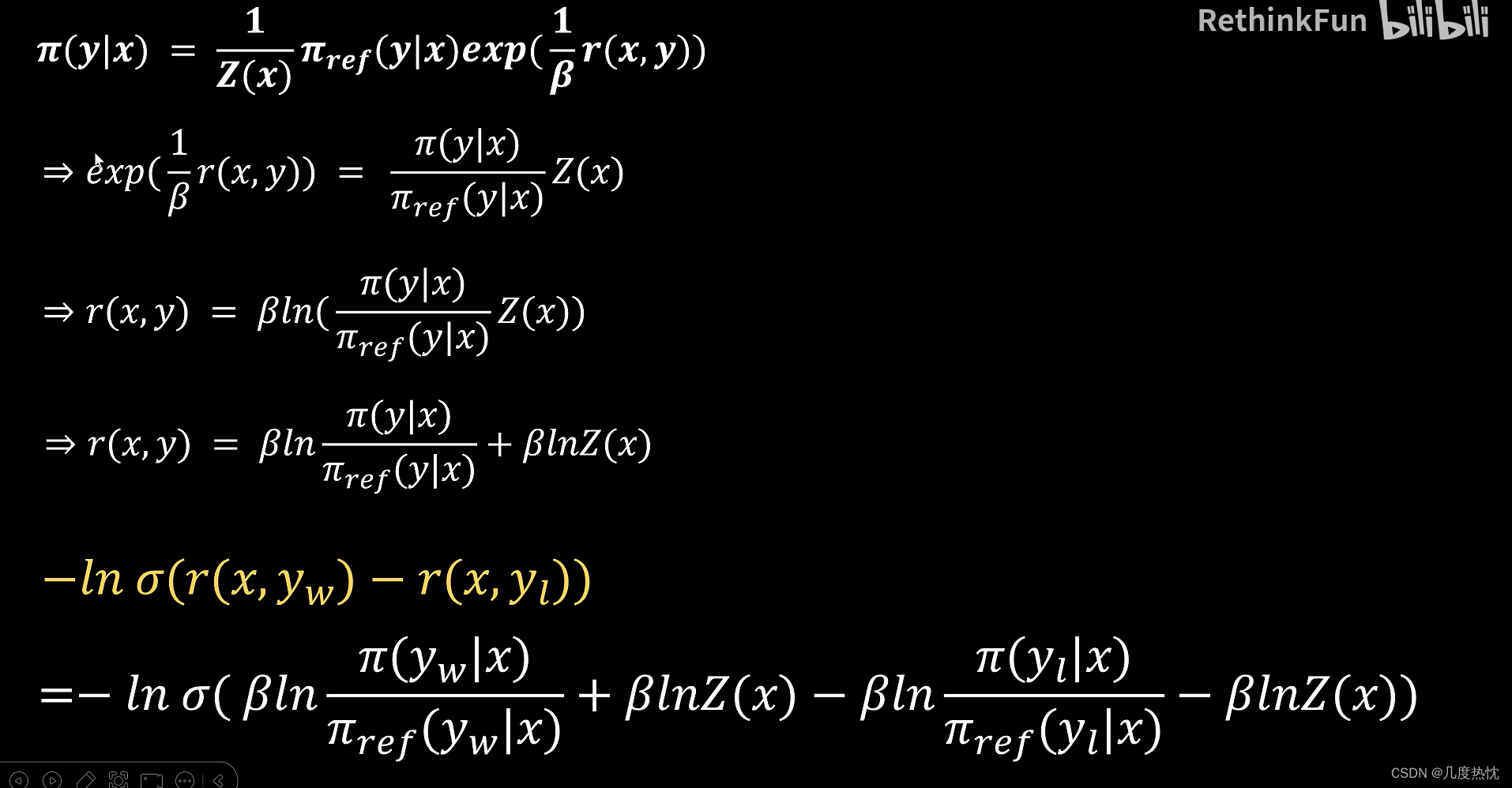
- DPO loss损失函数的表达形式
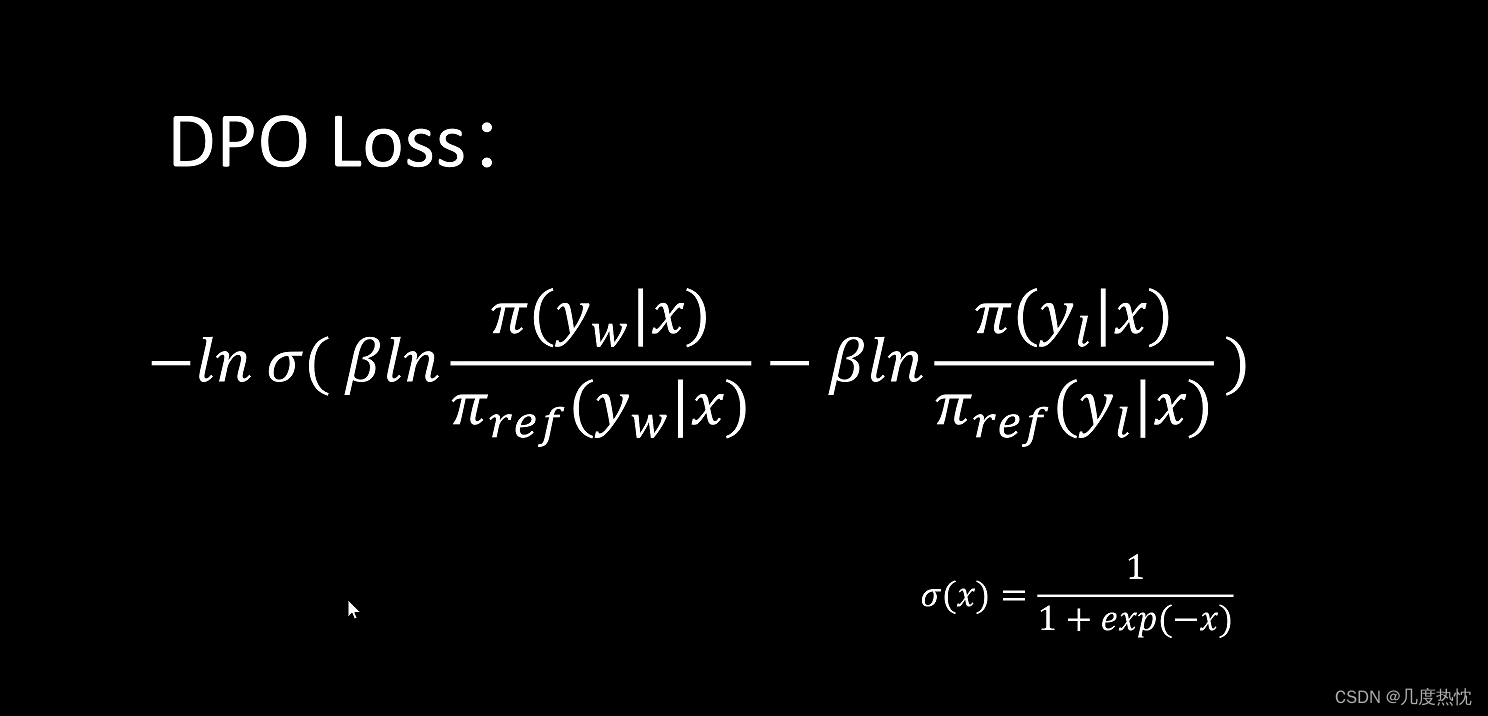
- logZ(x)项被抵消,于是可以转而用最大似然估计MLE直接在这个概率模型上直接优化LM,去得到希望的最优的π*
个人理解的一知半解 有时间还是得去看看原论文
参考文献
- DPO (Direct Preference Optimization) 算法讲解
- Direct Preference Optimization(DPO)学习笔记
- DPO原论文 Direct Preference Optimization: Your Language Model is Secretly a Reward Model
这篇关于【强化学习】DPO(Direct Preference Optimization)算法学习笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






