本文主要是介绍3.8 二叉树中结点最大的距离 重建二叉树 顺序遍历二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 前言
本文的一些图片, 资料 截取自编程之美
2. 问题描述
3. 问题分析
对于树的相关问题, 递归是非常常见的
对于第一个问题 : 可以通过先递归获取每一个结点的最大左子树的深度, 以及最大右子树的深度, 然后在递归一次获取(node.maxLeft + node.maxRight)的最大值即为所求
对于第二个问题, 因为我们现在有一个先序, 中序的遍历序列, 所以我们可以确定root结点即为先序遍历的第一个结点, 然后根据中序序列来确定root结点的左右子树, 然后在递归建树即可
对于第三个问题 , 通常是使用一个队列来维护需要遍历的结点队列, 遍历一个结点之后, 就将其左右孩子结点添加到队列中, 遍历啊遍历, 直到队列为空
对于上面的描述, 可能比较抽象, 下面是几幅图, 希望可以帮助理解
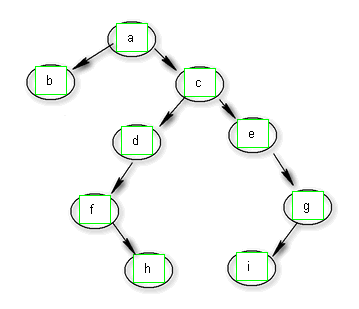
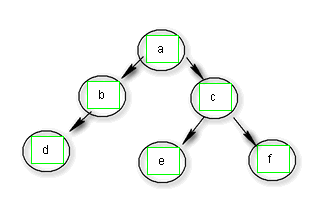
问题一 :
1 给定的树
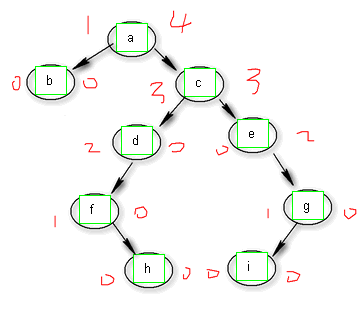
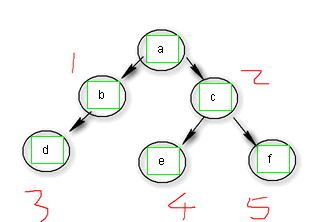
2 递归获取树的最大左右子树深度
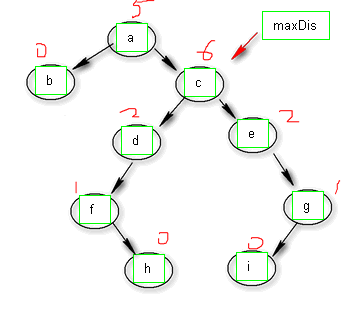
3 递归获取树的结点最大距离
问题二 :
1 前序和中序
firstOrder : 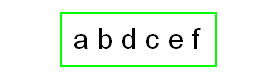
infixOrder :
2 判断根节点, 左右子树
根据firstOrder判断根节点 : 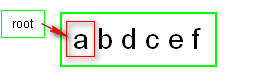
根据中序判断左右子树 : 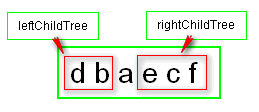
在根据左右子树的节点数, 分解前序中的左右子树 :
确定左右子树的前序, 中序遍历序列之后, 即可递归建树了
问题三 :
1 给定的树
2 将当前结点的左右结点添加到队列, 进队的顺序
进队的顺序就保证了层次关系, 因而层次遍历二叉树得以实现
4. 代码
备注 : 先序构建树, “#“结点表示空节点, 上面的问题三的图形对应的数的表示为 : a b # d # # c f # # e # #
代码清单 :
1 先序建树
2 先序 + 中序, 中序 + 后序, 重建二叉树 [一种思路是上面的思路, 另一种思路是先补全其先序序列[加上空结点], 然后在利用先序建树(1)[注意 : 中序 + 后序重建树, 需要先构建右子树, 然后在构建左子树 ], 不过原理和第一种基本上一致 ]
3 判断给定的先序 + 中序, 是否能够构建一颗二叉树
4 获取指定层级的结点
5 层次遍历, 层次自底向上遍历二叉树
/*** file name : Test09FindMaxDisInBinaryTree.java* created at : 8:56:46 AM May 29, 2015* created by 970655147*/package com.hx.test04;public class Test09FindMaxDisInBinaryTree {// 1. 获取一颗二叉树的两个节点的最大距离// 2. 重建二叉树// 3. 判断给定的(前序, 中序)[(中序, 后序) ] 是否能够成一个合法的二叉树// 4. 获取二叉树的某一层的元素// 5. 顺序遍历二叉树 层次遍历二叉树public static void main(String []args) {// BinTree bt = BinTree.createABinTree();
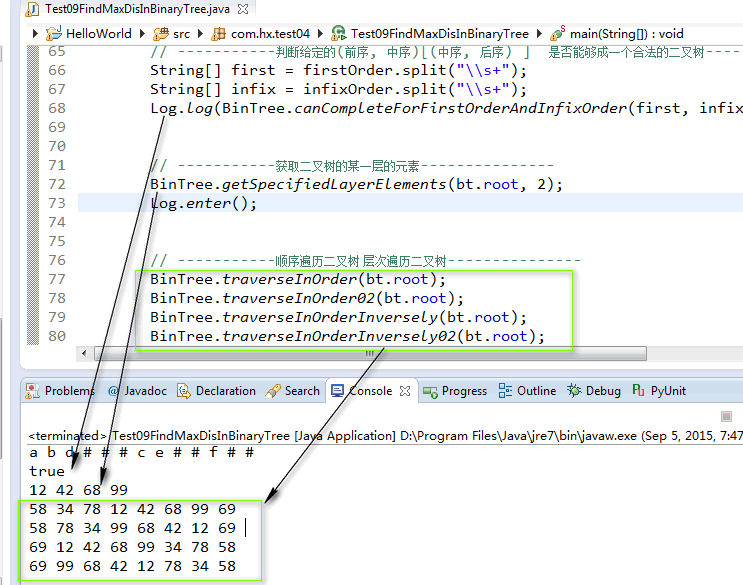
// Log.log(bt);// -----------获取一颗二叉树的两个节点的最大距离--------------- String data = "58 34 12 # # 42 # # 78 68 69 # # # 99 # #";BinTree bt = BinTree.createABinTree(data);Log.log(bt);List<Integer> deepth = new ArrayList<Integer>();bt.headTraverseForMaxDepth(bt.root, 0, deepth);Log.log(deepth );// 相信能获取到这个 数据的话应该知道 该怎么获取最大深度了吧,,int maxDis = bt.getMaxDis(bt.root);Log.log("maxDistance : " + maxDis);// -----------重建二叉树--------------- String data02 = "a b # d # # c f # # e # #";String firstOrder = "a b d c e f";String infixOrder = "d b a e c f";String epilogue = "d b e f c a";// BinTree bt02 = BinTree.rebuildForFirstOrderAndInfixOrder(firstOrder, infixOrder);
// BinTree bt02 = BinTree.rebuildForFirstOrderAndInfixOrder02(firstOrder, infixOrder);
// BinTree bt02 = BinTree.rebuildForInfixOrderAndEpilogue(infixOrder, epilogue);BinTree bt02 = BinTree.rebuildForInfixOrderAndEpilogue02(epilogue, infixOrder);Log.log(bt02);// -----------判断给定的(前序, 中序)[(中序, 后序) ] 是否能够成一个合法的二叉树--------------- String[] first = firstOrder.split("\\s+");String[] infix = infixOrder.split("\\s+");Log.log(BinTree.canCompleteForFirstOrderAndInfixOrder(first, infix, 0, 0, first.length) );// -----------获取二叉树的某一层的元素---------------BinTree.getSpecifiedLayerElements(bt.root, 2);Log.enter();// -----------顺序遍历二叉树 层次遍历二叉树---------------BinTree.traverseInOrder(bt.root);BinTree.traverseInOrder02(bt.root);BinTree.traverseInOrderInversely(bt.root);BinTree.traverseInOrderInversely02(bt.root);// -----------splits---------------}// 一颗二叉树public static class BinTree {// 根节点Node root;// 初始化public BinTree() {root = new Node();}public BinTree(Node root) {this.root = root;}// 获取root节点public Node root() {return root;}// 判断结点的左结点是否为空[#也算为空]public static boolean isNodeNull(Node node) {return (node == null) || (Node.NULL.equals(node.getData()) );}// 根据用户的输入创建一颗二叉树public static BinTree createABinTree() {BinTree bt = new BinTree();createNode(bt.root, "root");return bt;}// 根据指定格式的字符串创建一颗二叉树public static BinTree createABinTree(String data) {return createABinTreeReversely(data);}// 根据指定格式的字符串创建一颗二叉树 先建立左子树 在建立右子树public static BinTree createABinTreeReversely(String data) {BinTree bt = new BinTree();String[] splits = data.split("\\s+");idx = 0;createNodeReversely(bt.root, splits);return bt;}// 根据指定格式的字符串创建一颗二叉树 先建立右子树 在建立左子树public static BinTree epilogueOrderCreateABinTreeInversely(String data) {BinTree bt = new BinTree();String[] splits = data.split("\\s+");idx = 0;epilogueOrderCreateNodeInversely(bt.root, splits);return bt;}// assistMethod 根据用户的输入建树private static void createNode(Node node, String notice) {Scanner scan = Tools.getScanner();Log.logWithoutLn("please input " + notice + " : ");node.data = scan.next();if(!Node.NULL.equals(node.data) ) {node.left = new Node();node.right = new Node();createNode(node.left, notice + "'s leftChild");createNode(node.right, notice + "'s rightChild");}}// assistMethod 根据指定格式的字符串建树static int idx;// 先建立左子树 在建立右子树private static void createNodeReversely(Node node, String[] data) {node.data = data[idx ++];if(!Node.NULL.equals(node.data) ) {node.left = new Node();node.right = new Node();createNodeReversely(node.left, data);createNodeReversely(node.right, data);}}// 先建立右子树 在建立左子树private static void epilogueOrderCreateNodeInversely(Node node, String[] data) {node.data = data[idx ++];if(!Node.NULL.equals(node.data) ) {node.left = new Node();node.right = new Node();epilogueOrderCreateNodeInversely(node.right, data);epilogueOrderCreateNodeInversely(node.left, data);}}// 根据先序, 中序 重新建树// 思路 : 先补全树的字符串表示, 在建树[左 -> 右]public static BinTree rebuildForFirstOrderAndInfixOrder(String firstOrder, String infixOrder) {String[] first = firstOrder.split("\\s+");String[] infix = infixOrder.split("\\s+");StringBuilder sb = new StringBuilder();completeForFirstOrderAndInfixOrder(first, infix, 0, 0, first.length, sb);return createABinTree(sb.toString());}// 根据先序, 中序 重新建树 递归建树public static BinTree rebuildForFirstOrderAndInfixOrder02(String firstOrder, String infixOrder) {String[] first = firstOrder.split("\\s+");String[] infix = infixOrder.split("\\s+");Node root = rebuildForFirstOrderAndInfixOrder020(first, infix, 0, 0, first.length);return new BinTree(root);}// 根据中序, 后序 重新建树// 思路 : 先补全树的逆序字符串表示, 在逆序建树[右 -> 左]public static BinTree rebuildForInfixOrderAndEpilogue(String infixOrder, String epilogueOrder) {String[] epilogue = epilogueOrder.split("\\s+");String[] infix = infixOrder.split("\\s+");StringBuilder sb = new StringBuilder();completeForInfixOrderAndEpilogue(epilogue, infix, 0, 0, epilogue.length, sb);return epilogueOrderCreateABinTreeInversely(sb.toString());}// 根据先序, 中序 重新建树 递归建树public static BinTree rebuildForInfixOrderAndEpilogue02(String epilogueOrder, String infixOrder) {String[] epilogue = epilogueOrder.split("\\s+");String[] infix = infixOrder.split("\\s+");Node root = rebuildForInfixOrderAndEpilogueOrder020(epilogue, infix, 0, 0, infix.length);return new BinTree(root);}// 根据先序和中序 补全 "#"子节点private static void completeForFirstOrderAndInfixOrder(String[] first, String[] infix, int start01, int start02, int len, StringBuilder sb) {sb.append(first[start01] + " ");int idx = getIdxForStr(first[start01], infix, start02, len);int leftNumMinus1 = idx - start02, rightNumMinus1 = start02 + len - idx - 1;if(leftNumMinus1 == 0) {sb.append("# ");} else {completeForFirstOrderAndInfixOrder(first, infix, start01+1, start02, leftNumMinus1, sb);}if(rightNumMinus1 == 0) {sb.append("# ");} else {completeForFirstOrderAndInfixOrder(first, infix, start01+leftNumMinus1+1, idx+1, rightNumMinus1, sb);}}// 根据先序和中序, 递归构造左右子树private static Node rebuildForFirstOrderAndInfixOrder020(String[] first, String[] infix, int start01, int start02, int length) {Node node = new Node(first[start01]);int idx = getIdxForStr(first[start01], infix, start02, length);int leftNumMinus1 = idx - start02, rightNumMinus1 = start02 + length - idx - 1;if(leftNumMinus1 > 0) {node.left = rebuildForFirstOrderAndInfixOrder020(first, infix, start01+1, start02, leftNumMinus1);} else {node.left = new Node(Node.NULL);}if(rightNumMinus1 > 0) {node.right = rebuildForFirstOrderAndInfixOrder020(first, infix, start01+1+leftNumMinus1, idx+1, rightNumMinus1);} else {node.right = new Node(Node.NULL);}return node;}// 根据先序和中序 补全 "#"子节点private static void completeForInfixOrderAndEpilogue(String[] epilogue, String[] infix, int start01, int start02, int len, StringBuilder sb) {int endIdx = start01 + len - 1;sb.append(epilogue[endIdx] + " ");int idx = getIdxForStr(epilogue[endIdx], infix, start02, len);int leftNumMinus1 = idx - start02, rightNumMinus1 = start02 + len - idx - 1;if(rightNumMinus1 == 0) {sb.append("# ");} else {completeForInfixOrderAndEpilogue(epilogue, infix, endIdx-rightNumMinus1, idx+1, rightNumMinus1, sb);}if(leftNumMinus1 == 0) {sb.append("# ");} else {completeForInfixOrderAndEpilogue(epilogue, infix, start01, start02, leftNumMinus1, sb);}}// 根据中序和后序, 递归构造左右子树private static Node rebuildForInfixOrderAndEpilogueOrder020(String[] epilogue, String[] infix, int start01, int start02, int length) {int endIdx = start01 + length - 1;Node node = new Node(epilogue[endIdx]);int idx = getIdxForStr(epilogue[endIdx], infix, start02, length);int leftNumMinus1 = idx - start02, rightNumMinus1 = start02 + length - idx - 1;if(rightNumMinus1 > 0) {node.right = rebuildForInfixOrderAndEpilogueOrder020(epilogue, infix, start01+leftNumMinus1, idx+1, rightNumMinus1);} else {node.right = new Node(Node.NULL);}if(leftNumMinus1 > 0) {node.left = rebuildForInfixOrderAndEpilogueOrder020(epilogue, infix, start01, start02, leftNumMinus1);} else {node.left = new Node(Node.NULL);}return node;}// 判断给定的前序和中序 是否合理 是否能构成一颗合法的二叉树public static boolean canCompleteForFirstOrderAndInfixOrder(String[] first, String[] infix, int start01, int start02, int len) {int idx = getIdxForStr(first[start01], infix, start02, len);int leftNumMinus1 = idx - start02, rightNumMinus1 = start02 + len - idx - 1;boolean isLeftOk = false, isRightOk = false;if(leftNumMinus1 == 0) {isLeftOk = true;} else {isLeftOk = canCompleteForFirstOrderAndInfixOrder(first, infix, start01+1, start02, leftNumMinus1);}if(rightNumMinus1 == 0) {isRightOk = true;} else {isRightOk = canCompleteForFirstOrderAndInfixOrder(first, infix, start01+leftNumMinus1+1, idx+1, rightNumMinus1);}return isLeftOk && isRightOk;}// 获取level层的元素 递归实现public static void getSpecifiedLayerElements(Node node, int level) {if(Node.NULL.equals(node.data) ) {return ;}if(level == 0) {Log.logWithoutLn(node.data + " ");}getSpecifiedLayerElements(node.left, level-1);getSpecifiedLayerElements(node.right, level-1);}// 顺序遍历二叉树 方向从左至右public static void traverseInOrder(Node node) {Deque<Node> que = new LinkedList<Node>();que.addLast(node);while(que.size() > 0) {Node tmp = que.pollFirst();Log.logWithoutLn(tmp.data + " ");if(!Node.NULL.equals(tmp.left.data) ) {que.addLast(tmp.left);}if(!Node.NULL.equals(tmp.right.data) ) {que.addLast(tmp.right);}}Log.enter();}// 顺序遍历二叉树 方向从右至左public static void traverseInOrder02(Node node) {Deque<Node> que = new LinkedList<Node>();que.addLast(node);while(que.size() > 0) {Node tmp = que.pollFirst();Log.logWithoutLn(tmp.data + " ");if(!Node.NULL.equals(tmp.right.data) ) {que.addLast(tmp.right);}if(!Node.NULL.equals(tmp.left.data) ) {que.addLast(tmp.left);}}Log.enter();}// 顺序自底向上遍历二叉树 方向从左至右public static void traverseInOrderInversely(Node node) {Deque<Node> que = new LinkedList<Node>();Deque<Node> inv = new LinkedList<Node>();que.addLast(node);while(que.size() > 0) {Node tmp = que.pollFirst();inv.push(tmp);if(!Node.NULL.equals(tmp.right.data) ) {que.addLast(tmp.right);}if(!Node.NULL.equals(tmp.left.data) ) {que.addLast(tmp.left);}}while(inv.size() > 0) {Node tmp = inv.pop();Log.logWithoutLn(tmp.data + " ");}Log.enter();}// 顺序自底向上遍历二叉树 方向从右至左public static void traverseInOrderInversely02(Node node) {Deque<Node> que = new LinkedList<Node>();Deque<Node> inv = new LinkedList<Node>();que.addLast(node);while(que.size() > 0) {Node tmp = que.pollFirst();inv.push(tmp);if(!Node.NULL.equals(tmp.left.data) ) {que.addLast(tmp.left);}if(!Node.NULL.equals(tmp.right.data) ) {que.addLast(tmp.right);}}while(inv.size() > 0) {Node tmp = inv.pop();Log.logWithoutLn(tmp.data + " ");}Log.enter();}// 获取arr中与str相同的字符串的索引private static int getIdxForStr(String str, String[] arr, int start, int len) {int idx = -1, end = start + len;for(int i=start; i<end; i++) {if(str.equals(arr[i]) ) {idx = i;return idx;}}return idx;}// 先序遍历public void headTraverse(Node node) {if(node != null) {Log.logWithoutLn(node.data + " ");headTraverse(node.left);headTraverse(node.right);}}// assistMethod toString时使用 先序遍历二叉树 获取当前二叉树的字符串表示public void headTraverseForString(Node node, StringBuilder sb) {if(node != null) {sb.append(node.data + " ");
// sb.append(node.maxLeft + " - " + node.maxRight + "; ");headTraverseForString(node.left, sb);headTraverseForString(node.right, sb);}}// 先序遍历二叉树获取各个叶子节点的深度public void headTraverseForMaxDepth(Node node, int cnt, List<Integer> deepth) {if(! node.data.equals(Node.NULL) ) {headTraverseForMaxDepth(node.left, cnt+1, deepth);headTraverseForMaxDepth(node.right, cnt+1, deepth);} else {deepth.add(cnt);return ;}}// 先序遍历二叉树 获取每一个节点的最深左子树的深度, 和最深右子树的深度private void headTraverseForDepth(Node node, int cnt) {if(!node.data.equals(Node.NULL) ) {headTraverseForDepth(node.left, cnt+1);headTraverseForDepth(node.right, cnt+1);node.maxLeft = getMax(node.left.maxLeft + 1, node.left.maxRight + 1);node.maxRight = getMax(node.right.maxLeft + 1, node.right.maxRight + 1);} else {node.maxLeft = -1;node.maxRight = -1;return ;}}// 获取node子树的可能的最大距离 // 先递归获取每一个结点的最大左子树的深度, 以及最大右子树的深度, 然后在递归一次获取(node.maxLeft + node.maxRight)的最大值即为所求public int getMaxDis(Node node ) {headTraverseForDepth(node, 0);return getMaxDis0(node);}// 获取node子树的可能的最大距离 sum表示(maxLeft + maxRight)// 如果node.sum大于node.left.sum, node.right.sum 则结果去node.sum// 否则 去较大的子树结点 递归private int getMaxDis0(Node node ) {int nodeSum = node.maxLeft + node.maxRight;int nodeLeftSum = node.left.maxLeft + node.right.maxRight;int nodeRightSum = node.right.maxLeft + node.right.maxRight;int max = getMax(nodeSum, nodeLeftSum);max = getMax(max, nodeRightSum);if(max == nodeSum) {return nodeSum;} else if(max == nodeLeftSum) {return getMaxDis(node.left);} else if(max == nodeRightSum) {return getMaxDis(node.right);}return -1;}// 获取x, y的较大值private int getMax(int x, int y) {return x > y ? x : y;}// Debugpublic String toString() {StringBuilder sb = new StringBuilder();headTraverseForString(root, sb);return sb.toString();}}// 树的结点public static class Node {// 空节点 表示叶子节点final static String NULL = "#";// data 存放该节点的数据, left, right 存放左/ 右子树的索引// maxLeft, maxRight 表示左/ 右子树的最深深度String data;Node left;Node right;int maxLeft;int maxRight;// 初始化public Node() {} public Node(String data) {this.data = data;}// getter & setter public String getData() {return data;} public Node getLeft() {return left;}public Node getRight() {return right;}public void setLeft(Node left) {this.left = left;}public void setRight(Node right) {this.right = right;}// Debugpublic String toString() {return data;}}}
5. 运行结果
6. 总结
树是一种递归的结构, 所以涉及的算法很多都涉及递归, 通过这几个算法, 相信我们对于二叉树的了解又会深一层
这篇关于3.8 二叉树中结点最大的距离 重建二叉树 顺序遍历二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!