本文主要是介绍leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度
leecode 226 翻转二叉树
题目链接 :https://leetcode.cn/problems/invert-binary-tree/description/
题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
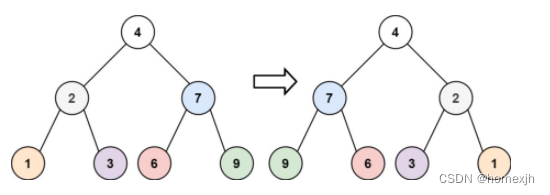
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
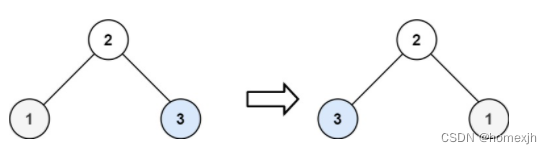
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
解题思路
这道题其实就是对二叉树的每个节点进行交换,其实就跟数值交换差不多,只不过这里是在二叉树。一般遇到二叉树相关题目,想一下使用哪一种遍历顺序,前中后。这道题来说,前序和后序基本都可以,如果是中序的话,某些节点可能要交换两次,因为中序遍历逻辑是左中右,在中进行交换,然后再遍历到右节点,这不是相当于把原来交换的再次交换了吗。具体实现代码为:
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) return root;traverseMid(root);return root;}public void traverse(TreeNode root) {if (root == null) return; //递归终止条件traverse(root.left); //左traverse(root.right); //右TreeNode tmp = root.left; //中root.left = root.right;root.right = tmp;}
}
//或者不用辅助函数
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) return root; //递归终止条件TreeNode left = invertTree(root.left); //左TreeNode right = invertTree(root.right); //右root.left = right; //中root.right = left;return root;}
}
leecode 101 对称二叉树
题目链接 :https://leetcode.cn/problems/symmetric-tree/description/
题目
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
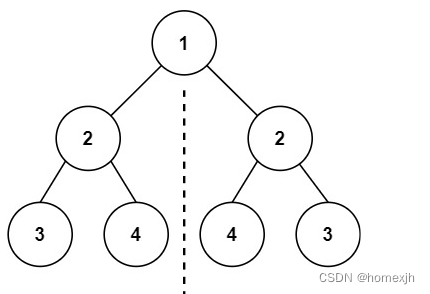
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
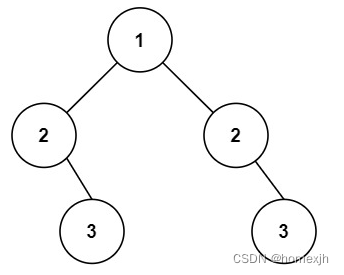
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
解题思路
这道题我们要清楚,要比较的不是左右节点,而是根节点的左右两棵树,所以在遍历的过程中,两棵树要同时遍历。那要哪种遍历顺序呢,因为同时比较两棵树的左右节点,那哪个遍历顺序通过返回值是能拿到左右节点信息的呢。就是后续遍历了。
那这道题的递归终止条件是什么呢,这道题是个判断题,一旦有符合的就直接返回。从示例中可以看到,左子树的左节点的值要等于右子树的右节点的值,左子树的右节点的值要等于右字数的左节点的值。所以这个是递归中的语句。那不满足的就是返回false就行了,递归条件有以下几种:
1.左子树为空右子树不为空 if (left == null && right != null) return false;
2.左子树不为空右子树为空 if (right == null && left != null) return false
3.左子树和右子树都为空,这是符合的 if (left == null && right == null) return true;
4.左子树的值不等于右子树的值 if (left.val != right.val) return false;
其中第4点一定是在前面三点判断完后开始判断,因为要不为空才有值。
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left,root.right); //两棵树同时遍历}public boolean compare(TreeNode left,TreeNode right) {if (left == null && right != null) return false; //1.左子树为空右子树不为空if (right == null && left != null) return false; //2.左子树不为空右子树为空if (left == null && right == null) return true; //3.左子树和右子树都为空if (left.val != right.val) return false; //4.左子树的值不等于右子树的值boolean out = compare(left.left,right.right); //左boolean inner = compare(left.right,right.left); //右return out && inner; //中}
}
leecode 104 二叉树的最大深度
题目链接 :https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
题目
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
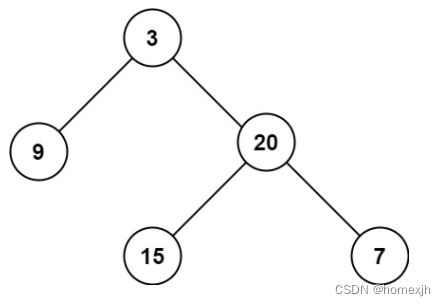
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100
解题思路
这道题用层序遍历可以套模板。这篇文章主要是说二叉树的递归。对于二叉树的最大深度,最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。那我们可以用前序遍历一路遍历下去,遍历到下一层,深度加一,不过要注意的是,在返回去的时候,深度要相应的减一,此时就涉及到回溯了。也可以用后序遍历,拿到左右值后深度加一。注意递归结束条件,是当root==null,return 0;取左右子树深度的最大值加上根节点这一层即可。当然,中序遍历也是一样的。具体代码为:
//后序遍历
class Solution {public int maxDepth(TreeNode root) { if (root == null) return 0; //递归终止条件int left = maxDepth(root.left); //左int right = maxDepth(root.right); //右return Math.max(left,right) + 1; //中}
}
//前序遍历
class Solution {int res = 0;public int maxDepth(TreeNode root) {int length = 0;traverse(root,length);return res;}public void traverse(TreeNode root,int length) {if (root == null) return;length++;res = Math.max(res,length); //中traverse(root.left,length); //左traverse(root.right,length); //右length--; //回溯}
}
//中序遍历
class Solution {int res = 0;public int maxDepth(TreeNode root) {int length = 0;traverse(root,length);return res;}public void traverse(TreeNode root,int length) {if (root == null) return;length++;traverse(root.left,length); //左res = Math.max(res,length); //中traverse(root.right,length); //右length--; //回溯}
}
这篇关于leecode 226 翻转二叉树、101 对称二叉树、104 二叉树的最大深度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



