代码随想录算法训练营第16天 |● 104.二叉树的最大深度 559.n叉树的最大深度 ● 111.二叉树的最小深度 ● 222.完全二叉树的节点个数

本文主要是介绍代码随想录算法训练营第16天 |● 104.二叉树的最大深度 559.n叉树的最大深度 ● 111.二叉树的最小深度 ● 222.完全二叉树的节点个数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

前言

所有的题目一刷都是优先掌握递归，迭代法没看，记不住。打十个做完之后再说吧
104和111没有看先序遍历的代码

104.二叉树的最大深度

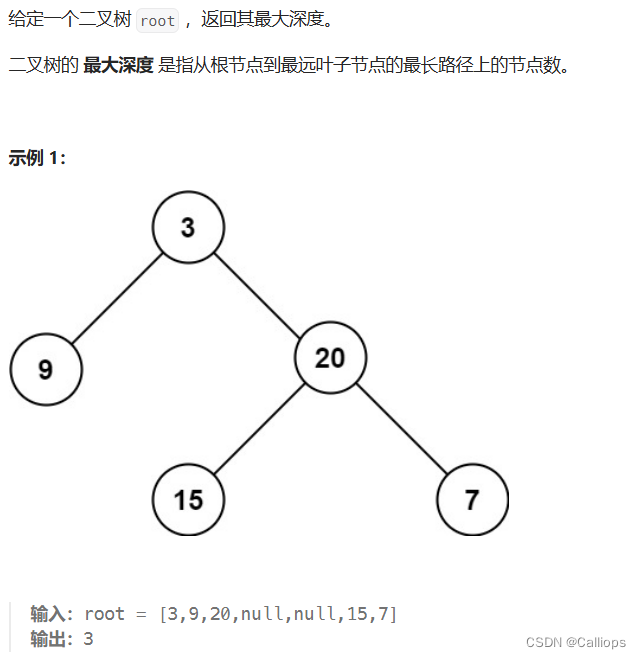
思路

知识点

记住深度和高度的定义：1. 从1开始 计数 2. 深度和高度与我们主观常识一致

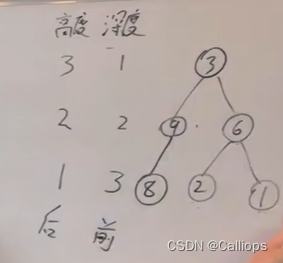
总体思路：求解最大深度就是求解根节点的高度；💛

因为求深度是前序遍历，求高度是后序遍历【在子节点的高度上加1就是根节点的高度】，后序遍历要比前序遍历在本题中简洁一些，所以本题使用后序遍历的求高度；
💟具体实现细节：单层递归中求解的逻辑是，当前节点的高度为子节点高度+1；【递归法的第三步】
递归三部曲

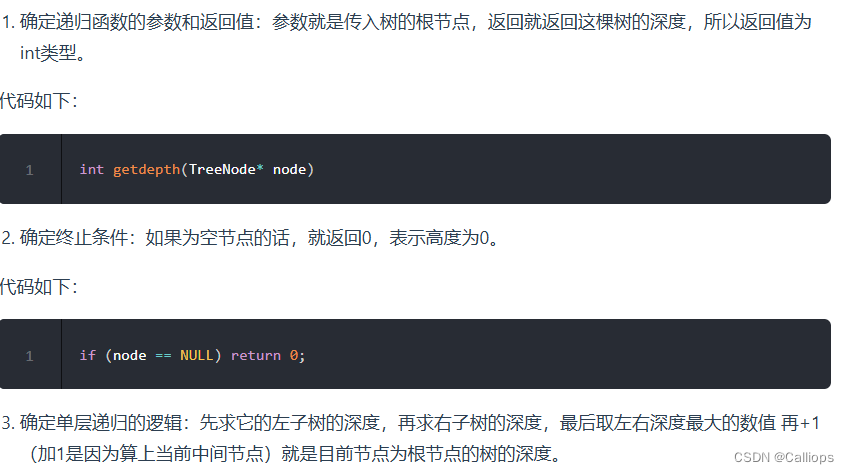
先序遍历有c++代码，非常直观的从上往下的递归。也可以看

方法一 递归法

class Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""def getheight(root):if not root: return 0height_left = getheight(root.left)height_right =getheight(root.right)height = 1+max(height_left,height_right)return heightreturn getheight(root)
###精简版
class Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""if not root: return 0return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

方法二 迭代法

559. n叉树的最大深度

这题目我也刷了

class Solution:def maxDepth(self, root: 'Node') -> int:if not root:return 0max_depth = 1for child in root.children:max_depth = max(max_depth, self.maxDepth(child) + 1)return max_depth

111.二叉树的最小深度

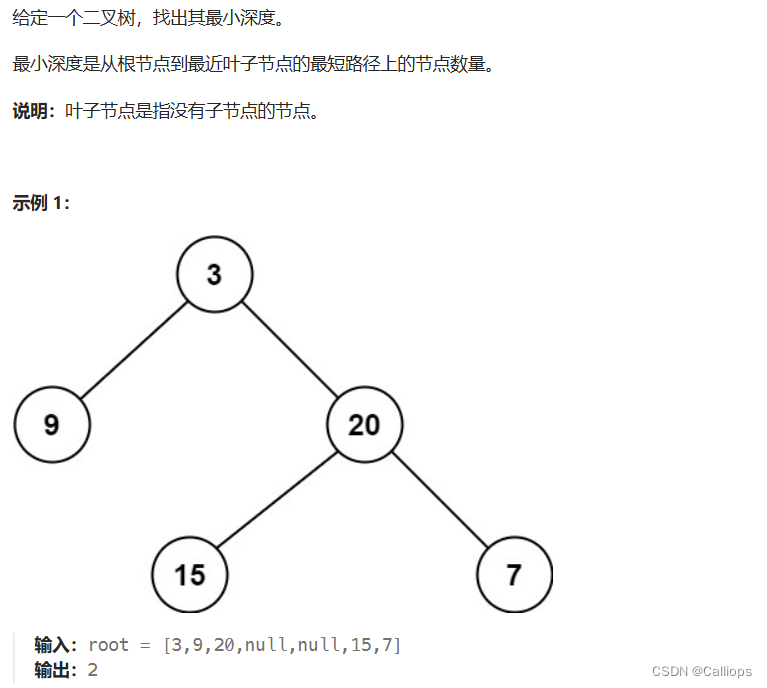
思路

总体思路：与上面的最大深度差不多，但是不能单纯将max改成min。

• 如果直接max改成min的话，例如下面的最右边的节点6会被算成高度为1，因为min子节点的结果为0，也就是将6当成叶子了；或者按照老师讲解的，根节点中会算左边的null为0.，这样最小深度就是1了。
  下面是老师的讲解
  

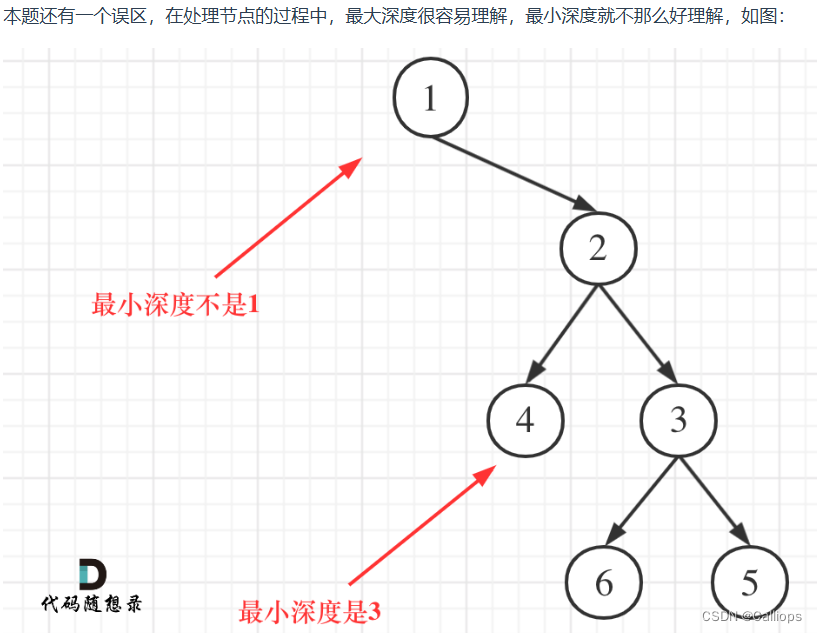
• 所以这条题目相较于104的改动就是加上分类讨论：（这是递归法的第三步单层逻辑）

  • 子节点中，一个是null，一个有节点，按照有节点的那个算
  • 两个都有的话选择min的那个
  • 两个都是空那就是0【可以与上面那个合并】
    

方法一 后向遍历递归法

自己写的错误

1. 在类里面调用递归的时候，记得加上self
2. 下面是教程里面的代码，我写的时候is None用not来代替了，我觉着这样国家好一些

class Solution:def getDepth(self, node):if node is None:return 0leftDepth = self.getDepth(node.left)  # 左rightDepth = self.getDepth(node.right)  # 右# 当一个左子树为空，右不为空，这时并不是最低点if node.left is None and node.right is not None:return 1 + rightDepth# 当一个右子树为空，左不为空，这时并不是最低点if node.left is not None and node.right is None:return 1 + leftDepthresult = 1 + min(leftDepth, rightDepth)return resultdef minDepth(self, root):return self.getDepth(root)### 精简代码
class Solution:def minDepth(self, root):if root is None:return 0if root.left is None and root.right is not None:return 1 + self.minDepth(root.right)if root.left is not None and root.right is None:return 1 + self.minDepth(root.left)return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

方法二 迭代法

222.完全二叉树的节点个数

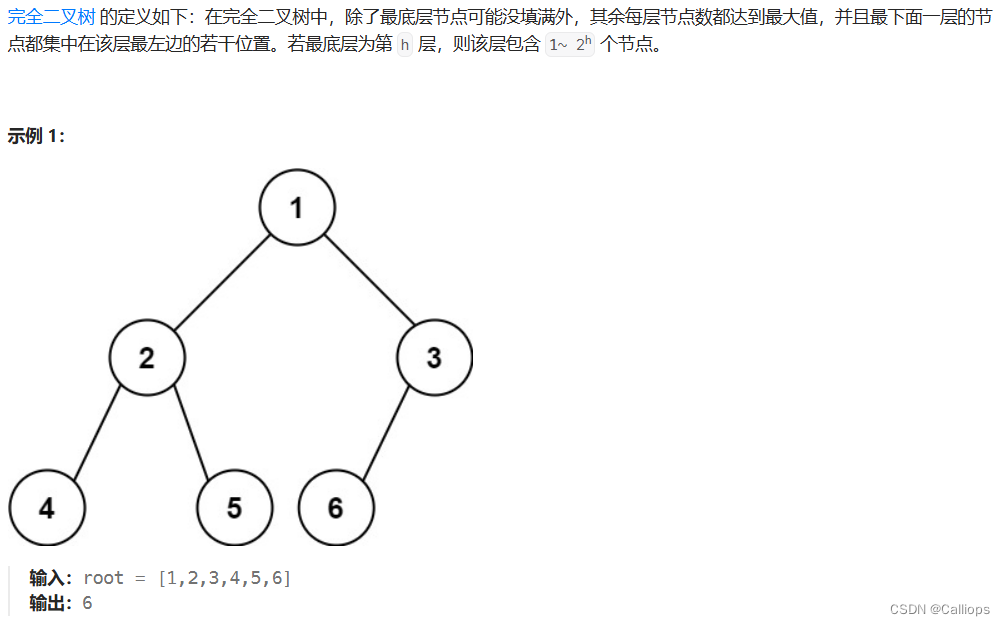
思路

方法一 当成普通二叉树来做

注意：使用后序遍历的代码是最简洁的
先序遍历：参考104题目教程里面的先序遍历写法，明显会复杂一些，为啥呢，因为需要一个全局变量来++1
单层处理逻辑：后序遍历到这个节点时，已经遍历的节点个数为它的子节点个数之和+1
递归三步走：

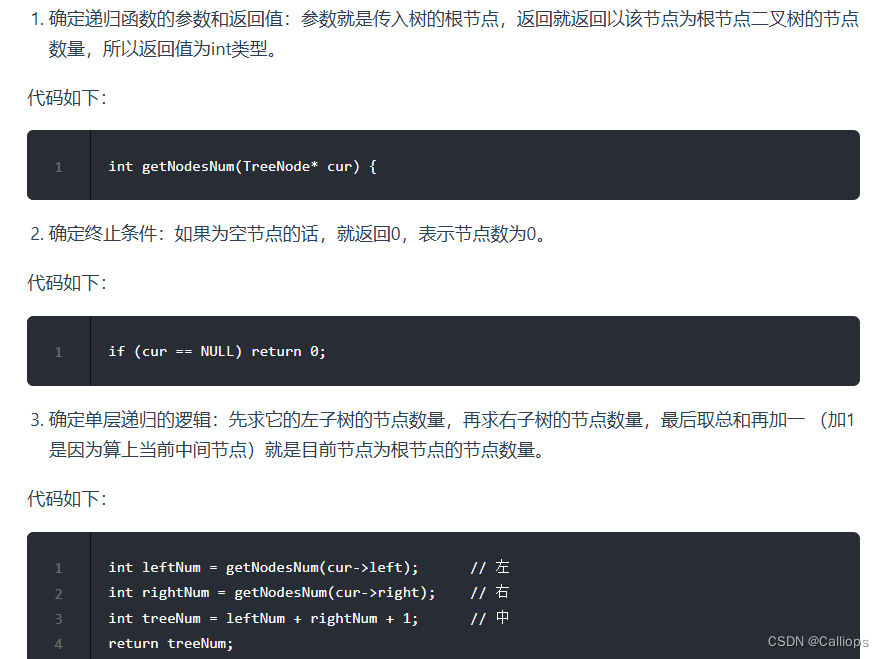
每一个都需遍历一下，时间复杂度为O(n)

class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""if not root: return 0cright = self.countNodes(root.right)cleft = self.countNodes(root.left)return 1+cright+cleft

方法二 利用完全二叉树的特性

首先回顾完全二叉树定义：

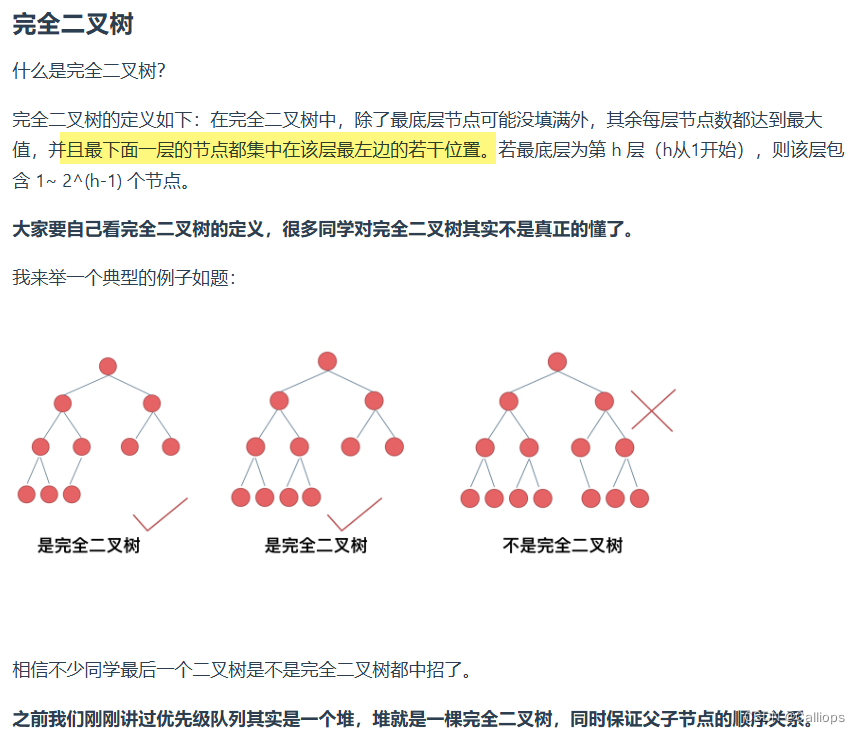
总体思路：利用满二叉树如果知道深度为n，节点个数就是2**n-1的特性，避免遍历所有的节点；
递归第三步单层处理逻辑：

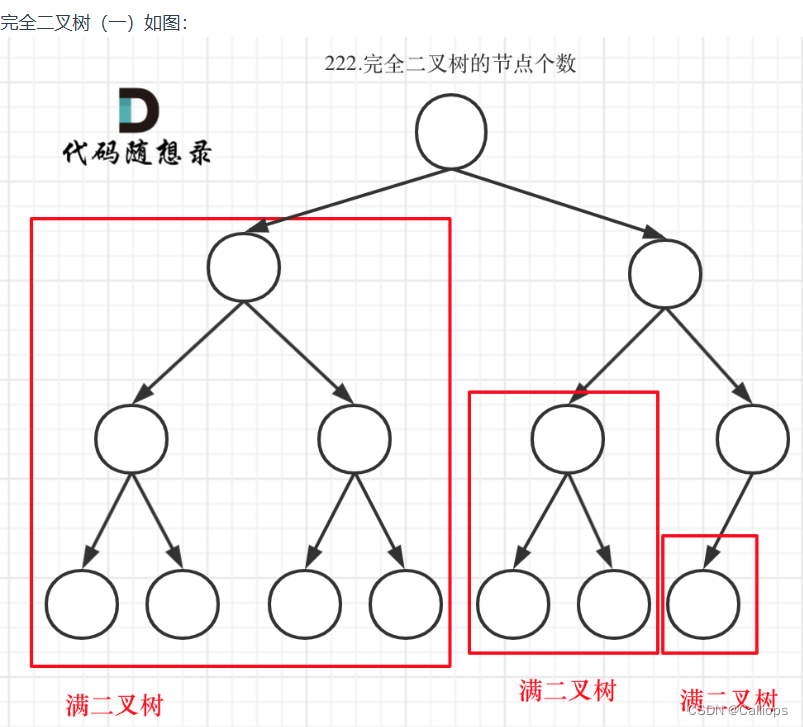
• 完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

  • 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

  • 对于情况二，左右孩子节点数之和加1

    • 左孩子，和右孩子的计算就是递归，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

    
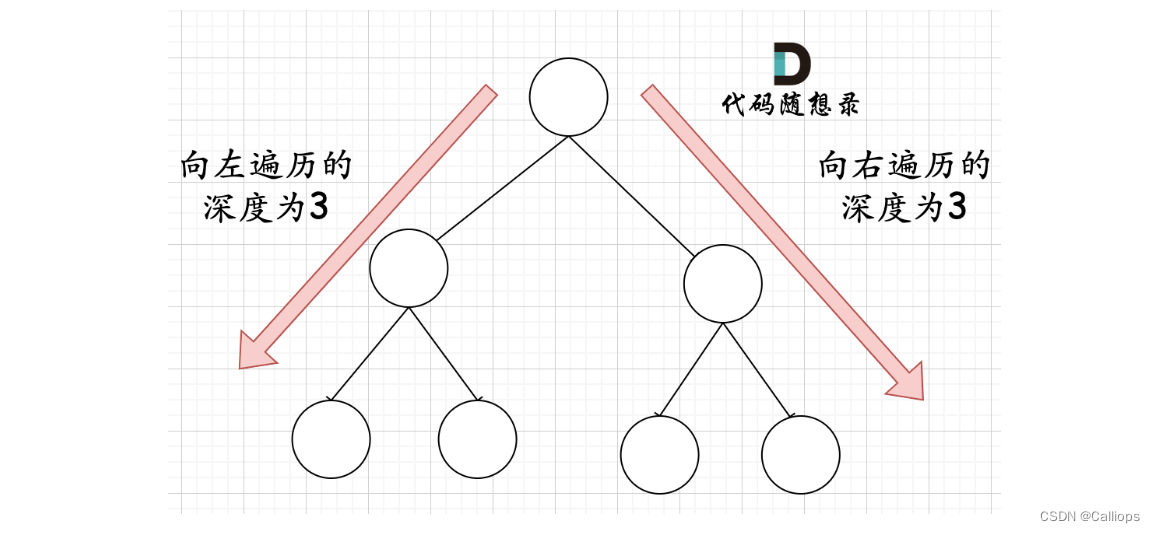
    如何判断是否为完全二叉树：最左边一层和最右边一层节点数相同，这样就只需要遍历最外侧的就行
    
    注意事项

1. left和right侧边count的起始为1
2. 2的阶数写为(2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0

class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""# if not root: return 0# cright = self.countNodes(root.right)# cleft = self.countNodes(root.left)# return 1+cright+cleftif not root: return 0#判断是否为满二叉树left = root.leftright = root.rightleft_height, right_height = 1,1# 注意这个是1while(left):left_height +=1left = left.leftwhile(right):right_height += 1right = right.rightif right_height == left_height:return 2**right_height -1cleft = self.countNodes(root.left)cright = self.countNodes(root.right)return 1+cleft+cright#还有一种技巧计算2的阶数，这时起始height要计算为0；代码如下，
class Solution:def countNodes(self, root: TreeNode) -> int:if not root:return 0left = root.leftright = root.rightleftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便rightDepth = 0while left: #求左子树深度left = left.leftleftDepth += 1while right: #求右子树深度right = right.rightrightDepth += 1if leftDepth == rightDepth:return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0return self.countNodes(root.left) + self.countNodes(root.right) + 1

更加简洁的写法：完全二叉树写法2【教程里面的】
两侧同时顺着边数，直到有一条边为none，然后依据是否同时到底来判断是否为满二叉树；

class Solution: # 利用完全二叉树特性def countNodes(self, root: TreeNode) -> int:if not root: return 0count = 1left = root.left; right = root.rightwhile left and right:count+=1left = left.left; right = right.rightif not left and not right: # 如果同时到底说明是满二叉树，反之则不是return 2**count-1return 1+self.countNodes(root.left)+self.countNodes(root.right) 

---

总结

比较有意思，今天都不想听申论课了。还是算法好玩。。。。可惜找不到工作

这篇关于代码随想录算法训练营第16天 |● 104.二叉树的最大深度 559.n叉树的最大深度 ● 111.二叉树的最小深度 ● 222.完全二叉树的节点个数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---