本文主要是介绍二叉树快速拾遗笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 二叉树前中后序遍历
- 反转二叉树
- 二叉树最大最小深度
- 对称二叉树
- 判断是否是平衡二叉树
- 构造最大二叉树
- 前序遍历打印二叉树
- 二叉树层次遍历
- 二叉树中和为某一值的路径
- 总结
前言
二叉树基础内容拾遗,使用递归解题三部曲:
- 找整个递归的终止条件: 递归应该在什么时候结束?
- 找返回值: 应该给上一级返回什么信息?
- 本级递归应该做什么:在这一级递归中应该完成什么任务?
提示:以下是本篇文章正文内容,下面案例可供参考
二叉树前中后序遍历
/*** 1. 前序遍历 根 左 右* 时间复杂度:O(n),其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。* 空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。**/public void preorderTraversal(TreeNode root) {if (root != null) {System.out.print(root.val + " "); preorderTraversal(root.left);preorderTraversal(root.right);}}/*** 中序:左 根 右** @param root* @return*/public void inorderTraversal(TreeNode root) {if (root != null) {inorderTraversal(root.left);System.out.print(root.val + " ");inorderTraversal(root.right);}}/*** 后序:左 右 根** @param root* @return*/public void postorderTraversal(TreeNode root) {if (root != null) {postorderTraversal(root.left);postorderTraversal(root.right);System.out.print(root.val + " ");}}
反转二叉树
- 递归实现
public TreeNode invertTree(TreeNode node) {if (node == null) {return null;}TreeNode temp = node.left;node.left = node.right;node.right = temp;invertTree(node.left);invertTree(node.right);return node;}
- 非递归队列实现
public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();TreeNode left = node.left;node.left = node.right;node.right = left;if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}return root;}
二叉树最大最小深度
/*** 最大深度*/public static int treeMaxDepth(TreeNode curr) {if (curr != null) {int left = treeMaxDepth(curr.left);int right = treeMaxDepth(curr.right);return left > right ? left + 1 : right + 1;}return 0;}/*** 最小深度*/public static int treeMinDepth(TreeNode root) {TreeNode curr = root;if (curr == null) return 0;if (curr.left == null && curr.right == null) return 1;int min_depth = Integer.MAX_VALUE;if (curr.left != null) {min_depth = Math.min(treeMinDepth(curr.left), min_depth);}if (curr.right != null) {min_depth = Math.min(treeMinDepth(curr.right), min_depth);}return min_depth + 1;}
对称二叉树
/*** 递归解决* <p>* 时间复杂度:O(n)O(n),因为我们遍历整个输入树一次,所以总的运行时间为 O(n)O(n),其中 nn 是树中结点的总数。* 空间复杂度:递归调用的次数受树的高度限制。在最糟糕情况下,树是线性的,其高度为 O(n)O(n)。因此,在最糟糕的情况下,由栈上的递归调用造成的空间复杂度为 O(n)O(n)。** @param root* @return*/public boolean isSymmetric(TreeNode root) {return isMirror(root, root);}public boolean isMirror(TreeNode left, TreeNode right) {if (left == null && right == null) return true;if (left == null || right == null) return false;return (left.val == right.val) && isMirror(left.left, right.right) && isMirror(left.right, right.left);}
判断是否是平衡二叉树
平衡二叉树即左右两棵子树高度差不大于1的二叉树。
条件:
它的左子树是平衡二叉树,
它的右子树是平衡二叉树,
它的左右子树的高度差不大于1。
在我们眼里,这颗二叉树就3个节点:root、left、right
/*** 递归解决,计算子树高度,-1表示子树已经不平衡了*/
class Solution2 {public boolean isBalanced(TreeNode root) {return height(root) >= 0;}private int height(TreeNode root) {if (root == null)return 0;int lh = height(root.left), rh = height(root.right);if (lh >= 0 && rh >= 0 && Math.abs(lh - rh) <= 1) {return Math.max(lh, rh) + 1;} else {return -1;}}
构造最大二叉树
https://leetcode-cn.com/problems/maximum-binary-tree/
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下:
二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。
一次递归做了什么?
找当前范围为[l,r]的数组中的最大值作为root节点,然后将数组划分成[l,bond-1]和[bond+1,r]两段,并分别构造成root的左右两棵子最大二叉树
public class _654_最大二叉树 {public static void main(String[] args) {int[] arr = new int[]{3, 2, 1, 6, 0, 5};TreeNode treeNode = new _654_最大二叉树().constructMaximumBinaryTree(arr);ArrayList<Integer> list = TreeNode.printFromTopToBottom(treeNode);System.out.println(list);}public TreeNode constructMaximumBinaryTree(int[] nums) {return maxTree(nums, 0, nums.length - 1);}public TreeNode maxTree(int[] nums, int l, int r) {//1. 判断边界条件 当左边大于右边的时候返回NULL;if (l > r) return null;//2. 找出最大值索引值int maxIndex = findMaxIndex(nums, l, r);//3.以最大值新建树顶TreeNode root = new TreeNode(nums[maxIndex]);//4.分别递归左右子树root.left = maxTree(nums, l, maxIndex - 1);root.right = maxTree(nums, maxIndex + 1, r);//5.返回根节点return root;}public int findMaxIndex(int[] nums, int l, int r) {// 初始化最小值和最小indexint max = Integer.MIN_VALUE, maxIndex = l;// 注意这里的遍历的起点和终点的判断条件for (int i = l; i <= r; i++) {if (max < nums[i]) {max = nums[i];maxIndex = i;}}return maxIndex;}
}
前序遍历打印二叉树
/*** 前序打印二叉树 (根->左->右)* @param root* @return*/public static ArrayList<Integer> printFromTopToBottom(TreeNode root) {ArrayList<Integer> arrayList = new ArrayList<Integer>();if (root==null){return arrayList;}Queue<TreeNode> queue = new LinkedList<TreeNode>();//队列:先入先出//将树存入队列中 根、左、右queue.offer(root);//添加根:add()和remove()方法在失败的时候会抛出异常(不推荐),offer代替while (!queue.isEmpty()){TreeNode node= queue.poll();//树当前节点更新;poll()返回第一个元素,并在队列中删除arrayList.add(node.val);//保存当前节点if (node.left!=null){queue.offer(node.left);//左}if (node.right!=null){queue.offer(node.right);//右}}return arrayList;}
二叉树层次遍历
示例:
二叉树:[3,9,20,null,null,15,7],3/ \9 20/ \15 7
返回其层序遍历结果:[[3],[9,20],[15,7]
]
链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal
/*** 时间复杂度:每个点进队出队各一次,故渐进时间复杂度为 O(n)* 空间复杂度:队列中元素的个数不超过 n个,故渐进空间复杂度为 O(n)* @param root* @return*/public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<>();if (root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> list = new ArrayList<>();int currentLevelSize = queue.size();for (int i = 1; i <= currentLevelSize; ++i) {TreeNode node = queue.poll();list.add(node.val);if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}ret.add(list);}return ret;}
二叉树中和为某一值的路径
参考:https://www.cnblogs.com/lishanlei/p/10707709.html
由于路径是从根节点出发到叶子节点的,因此我们需要首先遍历根节点,只有前序遍历是首先访问根节点的。
当访问某一个节点时,我们不知道前面经过了哪些节点,所以我们需要将经过的路径上的节点保存下来,每访问一个节点,我们需要把当前节点添加到路径中去。
在遍历下一个节点前,先要回到当前节点的父节点,在去其他节点,当回到父节点时,之前遍历的那个节点已经不在当前路径中了,所以需要删除之前在路径中的那个节点。
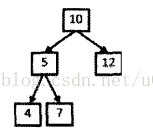
public List<ArrayList<Integer>> FindPath(TreeNode root, int target) {List<ArrayList<Integer>> listAll = new ArrayList<>(); //保存所有符合条件的路径用于返回值List<Integer> list = new ArrayList<>(); //存储当前路径return SeekPath(listAll, list, root, target);}private List<ArrayList<Integer>> SeekPath(List<ArrayList<Integer>> listAll, List<Integer> list, TreeNode root, int target) {if (root == null) return listAll;list.add(root.val);target -= root.val;if (target == 0 && root.left == null && root.right == null) { //当前路径和是指定值且当前节点是叶子节点listAll.add(new ArrayList<>(list));}SeekPath(listAll, list, root.left, target);SeekPath(listAll, list, root.right, target);list.remove(list.size() - 1); //递归回到父节点时需要在路径中删除上一个节点信息return listAll;}// FindPath(tree, 22) output: [[10, 5, 7], [10, 12]]
总结
未完待续
这篇关于二叉树快速拾遗笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





