C语言还可以这么玩，你绝对想不到！

2024-05-18 17:48
文章标签 语言 绝对 想不到

本文主要是介绍C语言还可以这么玩，你绝对想不到！，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

点击上方“小麦大叔”，选择“置顶/星标公众号”

福利干货，第一时间送达

大家好，我是小麦，又到了愉快的周五，有人说程序员就是艺术家，那下面我们看看用c语言能画出什么作品吧。

6421b43e791c40efec89d1c570e03d08.png

我们知道，在计算机中要显示颜色，一般都是用R、G、B三个0-255范围内的整数来描述。

5d9dfac927d11480e8eb0e6accf52978.png

这一点，即便你不是从事前端、客户端这些与界面交互相关的开发工作，也应该知道。

也就是说，你现在在屏幕上看到的任何一个像素点的颜色，都可以用RGB三个整数值来表示。

那就有一个有趣的问题：如果让程序自动来填写每一个像素点，最后会是一副什么画呢？

最近，我在知乎就看到了这么一个有趣的话题，看完真的让人称奇，独乐乐不如众乐乐，分享给大家。

事情是这样的：

国外有个大佬在StackExchange上发起了一个叫做 Tweetable Mathematical Art 的比赛。

参赛者需要用C/C++编写代表三原色的RD、GR、BL三个函数，每个函数都不能超过 140 个字符。每个函数都会接到 i 和 j 两个整型参数（0 ≤ i, j ≤ 1023），然后需要返回一个 0 到 255 之间的整数，表示位于 (i, j) 的像素点的颜色值。

举个例子，如果 RD(0, 0) 和 GR(0, 0) 返回的都是 0 ，但 BL(0, 0) 返回的是 255 ，那么图像的最左上角那个像素就是蓝色。

参赛者编写的代码会被插进下面这段程序当中（我做了一些细微的改动），最终会生成一个大小为 1024×1024 的图片。

// NOTE: compile with g++ filename.cpp -std=c++11
#include <iostream>
#include <cmath>
#include <cstdlib>
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // square
#define _cb(x) abs((x)*(x)*(x)) // absolute value of cube
#define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // cube rootunsigned char GR(int,int);
unsigned char BL(int,int);unsigned char RD(int i,int j){// YOUR CODE HERE
}
unsigned char GR(int i,int j){// YOUR CODE HERE
}
unsigned char BL(int i,int j){// YOUR CODE HERE
}void pixel_write(int,int);
FILE *fp;
int main(){fp = fopen("MathPic.ppm","wb");fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM);for(int j=0;j<DIM;j++)for(int i=0;i<DIM;i++)pixel_write(i,j);fclose(fp);return 0;
}
void pixel_write(int i, int j){static unsigned char color[3];color[0] = RD(i,j)&255;color[1] = GR(i,j)&255;color[2] = BL(i,j)&255;fwrite(color, 1, 3, fp);
}

我选了一些自己比较喜欢的作品，放在下面和大家分享。首先，是一个来自 Martin Büttner 的作品：

336d3629cf3fbc555b24623ec8cbf538.png

它的代码如下：

unsigned char RD(int i,int j){return (char)(_sq(cos(atan2(j-512,i-512)/2))*255);
}unsigned char GR(int i,int j){return (char)(_sq(cos(atan2(j-512,i-512)/2-2*acos(-1)/3))*255);
}unsigned char BL(int i,int j){return (char)(_sq(cos(atan2(j-512,i-512)/2+2*acos(-1)/3))*255);
}

这同样是来自 Martin Büttner 的作品：

fdf6f3ea81680fd4bc5e25a73ba710d8.png

这是目前暂时排名第一的作品，它的代码如下：

unsigned char RD(int i,int j){#define r(n)(rand()%n)static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):RD((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}unsigned char GR(int i,int j){static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):GR((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}unsigned char BL(int i,int j){static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):BL((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}

下面这张图仍然出自 Martin Büttner 之手：

f0f57c951bffc8c4685348462ca57cb6.png

难以想象， Mandelbrot 分形图形居然可以只用这么一点代码画出：

unsigned char RD(int i,int j){float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}return log(k)*47;
}unsigned char GR(int i,int j){float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}return log(k)*47;
}unsigned char BL(int i,int j){float x=0,y=0;int k;for(k=0;k++<256;){float a=x*x-y*y+(i-768.0)/512;y=2*x*y+(j-512.0)/512;x=a;if(x*x+y*y>4)break;}return 128-log(k)*23;
}

Manuel Kasten 也制作了一个 Mandelbrot 集的图片，与刚才不同的是，该图描绘的是 Mandelbrot 集在某处局部放大后的结果：

2c10895da0d16d6b839ff1c2b3235d7e.png

它的代码如下：

unsigned char RD(int i,int j){double a=0,b=0,c,d,n=0;while((c=a*a)+(d=b*b)<4&&n++<880){b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}return 255*pow((n-80)/800,3.);
}unsigned char GR(int i,int j){double a=0,b=0,c,d,n=0;while((c=a*a)+(d=b*b)<4&&n++<880){b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}return 255*pow((n-80)/800,.7);
}unsigned char BL(int i,int j){double a=0,b=0,c,d,n=0;while((c=a*a)+(d=b*b)<4&&n++<880){b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}return 255*pow((n-80)/800,.5);
}

这是 Manuel Kasten 的另一作品：

bf4bf24eec752a43935da0b65a2603fa.png

生成这张图片的代码很有意思：函数依靠 static 变量来控制绘画的进程，完全没有用到 i 和 j 这两个参数！

unsigned char RD(int i,int j){static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}unsigned char GR(int i,int j){static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}unsigned char BL(int i,int j){static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}

这是来自 githubphagocyte 的作品：

7b103096a693725f5ea10964e5129286.png

它的代码如下：

unsigned char RD(int i,int j){float s=3./(j+99);float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127;
}unsigned char GR(int i,int j){float s=3./(j+99);float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127;
}unsigned char BL(int i,int j){float s=3./(j+99);float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127;
}

这是来自 githubphagocyte 的另一个作品：

9d079bd56c570c186090cd5a838383e5.png

这是一张使用 diffusion-limited aggregation 模型得到的图片，程序运行起来要耗费不少时间。

代码很有意思：巧妙地利用宏定义，打破了函数与函数之间的界限，三段代码的字数限制便能合在一起使用了。

unsigned char RD(int i,int j){
#define D DIM
#define M m[(x+D+(d==0)-(d==2))%D][(y+D+(d==1)-(d==3))%D]
#define R rand()%D
#define B m[x][y]
return(i+j)?256-(BL(i,j))/2:0;
}unsigned char GR(int i,int j){
#define A static int m[D][D],e,x,y,d,c[4],f,n;if(i+j<1){for(d=D*D;d;d--){m[d%D][d/D]=d%6?0:rand()%2000?1:255;}for(n=1
return RD(i,j);
}unsigned char BL(int i,int j){
A;n;n++){x=R;y=R;if(B==1){f=1;for(d=0;d<4;d++){c[d]=M;f=f<c[d]?c[d]:f;}if(f>2){B=f-1;}else{++e%=4;d=e;if(!c[e]){B=0;M=1;}}}}}return m[i][j];
}

最后这张图来自 Eric Tressler：

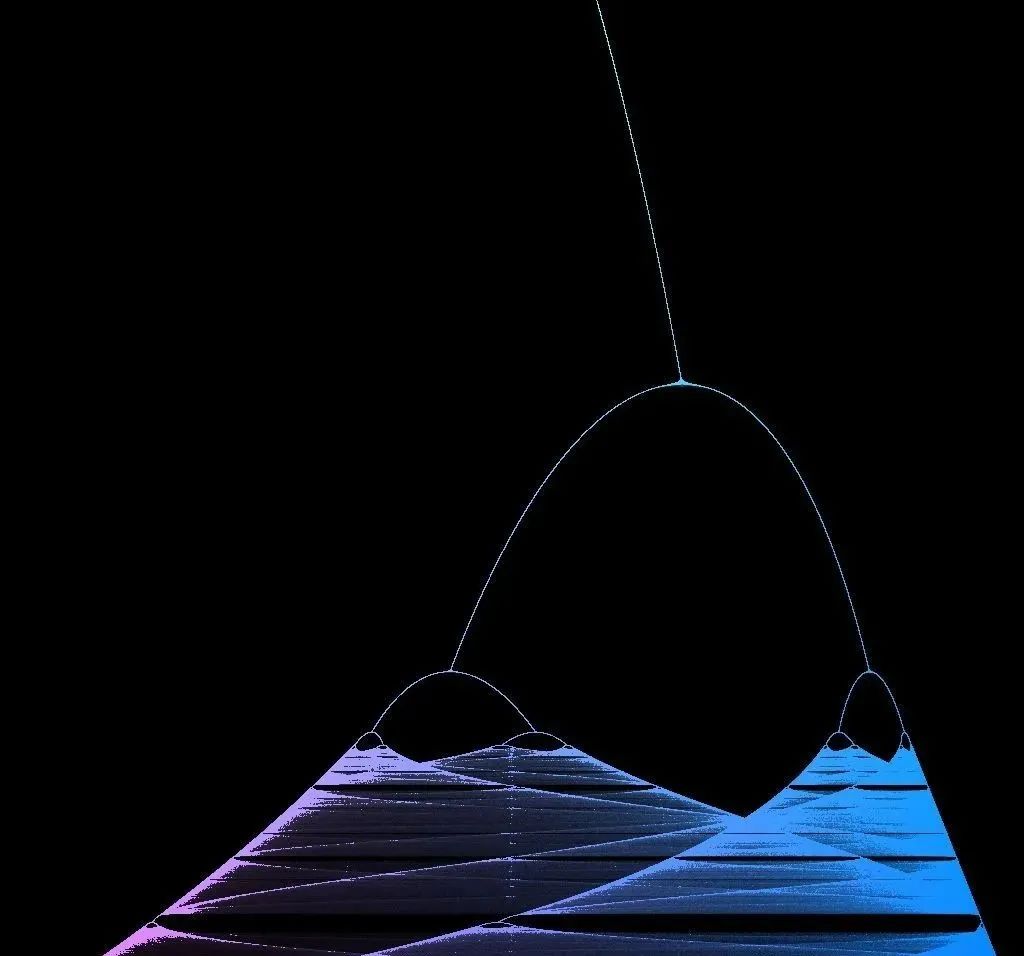
72d0bfbcf7fa299b2c9f01bdcfcbe529.png

这是由 logistic 映射得到的 Feigenbaum 分岔图。和刚才一样，对应的代码也巧妙地利用了宏定义来节省字符：

unsigned char RD(int i,int j){
#define A float a=0,b,k,r,x
#define B int e,o
#define C(x) x>255?255:x
#define R return
#define D DIM
R BL(i,j)*(D-i)/D;
}unsigned char GR(int i,int j){
#define E DM1
#define F static float
#define G for(
#define H r=a*1.6/D+2.4;x=1.0001*b/D
R BL(i,j)*(D-j/2)/D;
}unsigned char BL(int i,int j){
F c[D][D];if(i+j<1){A;B;G;a<D;a+=0.1){G b=0;b<D;b++){H;G k=0;k<D;k++){x=r*x*(1-x);if(k>D/2){e=a;o=(E*x);c[e][o]+=0.01;}}}}}R C(c[j][i])*i/D;
}

怎么样，短短几行代码，就能画出如此绚烂的图像，你有没有什么脑洞大开的想法，可以复制上面的代码来试一试啊！

作者：烧茄子

原文地址：www.zhihu.com/question/30262900/answer/48741026

版权归原作者所有，如有侵权，请联系删除。

—— The End ——

往期推荐

好项目，不私藏！适用于单片机开发的开源轮子

单片机开发从来不用数据结构？

写烂代码的人离职之后...

难倒高手了，c语言枚举end的作用是什么？

加入嵌入式技术交流群一起进步

点击上方名片关注我

f8597695d1d375ec8216e9b8d0785921.png

你点的每个好看，我都认真当成了喜欢

这篇关于C语言还可以这么玩，你绝对想不到！的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/995613。

相关文章

C语言中位操作的实际应用举例

C语言中位操作的实际应用举例

《C语言中位操作的实际应用举例》：本文主要介绍C语言中位操作的实际应用,总结了位操作的使用场景,并指出了需要注意的问题,如可读性、平台依赖性和溢出风险,文中通过代码介绍的非常详细,需要的朋友可以参... 目录1. 嵌入式系统与硬件寄存器操作2. 网络协议解析3. 图像处理与颜色编码4. 高效处理布尔标志集合
阅读更多...
Go语言开发实现查询IP信息的MCP服务器

Go语言开发实现查询IP信息的MCP服务器

《Go语言开发实现查询IP信息的MCP服务器》随着MCP的快速普及和广泛应用,MCP服务器也层出不穷,本文将详细介绍如何在Go语言中使用go-mcp库来开发一个查询IP信息的MCP... 目录前言mcp-ip-geo 服务器目录结构说明查询 IP 信息功能实现工具实现工具管理查询单个 IP 信息工具的实现服
阅读更多...
C 语言中enum枚举的定义和使用小结

C 语言中enum枚举的定义和使用小结

《C语言中enum枚举的定义和使用小结》在C语言里,enum（枚举）是一种用户自定义的数据类型,它能够让你创建一组具名的整数常量,下面我会从定义、使用、特性等方面详细介绍enum,感兴趣的朋友一起看... 目录1、引言2、基本定义3、定义枚举变量4、自定义枚举常量的值5、枚举与switch语句结合使用6、枚
阅读更多...
Go 语言中的select语句详解及工作原理

Go 语言中的select语句详解及工作原理

《Go语言中的select语句详解及工作原理》在Go语言中,select语句是用于处理多个通道（channel）操作的一种控制结构,它类似于switch语句,本文给大家介绍Go语言中的select语... 目录Go 语言中的 select 是做什么的基本功能语法工作原理示例示例 1：监听多个通道示例 2：带
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
C语言中的数据类型强制转换

C语言中的数据类型强制转换

《C语言中的数据类型强制转换》：本文主要介绍C语言中的数据类型强制转换方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C语言数据类型强制转换自动转换强制转换类型总结C语言数据类型强制转换强制类型转换：是通过类型转换运算来实现的，主要的数据类型转换分为自动转换
阅读更多...
利用Go语言开发文件操作工具轻松处理所有文件

利用Go语言开发文件操作工具轻松处理所有文件

《利用Go语言开发文件操作工具轻松处理所有文件》在后端开发中,文件操作是一个非常常见但又容易出错的场景,本文小编要向大家介绍一个强大的Go语言文件操作工具库,它能帮你轻松处理各种文件操作场景... 目录为什么需要这个工具？核心功能详解1. 文件/目录存javascript在性检查2. 批量创建目录3. 文件
阅读更多...
C语言实现两个变量值交换的三种方式

C语言实现两个变量值交换的三种方式

《C语言实现两个变量值交换的三种方式》两个变量值的交换是编程中最常见的问题之一,以下将介绍三种变量的交换方式,其中第一种方式是最常用也是最实用的,后两种方式一般只在特殊限制下使用,需要的朋友可以参考下... 目录1.使用临时变量（推荐）2.相加和相减的方式（值较大时可能丢失数据）3.按位异或运算1.使用临时
阅读更多...
使用C语言实现交换整数的奇数位和偶数位

使用C语言实现交换整数的奇数位和偶数位

《使用C语言实现交换整数的奇数位和偶数位》在C语言中,要交换一个整数的二进制位中的奇数位和偶数位,重点需要理解位操作,当我们谈论二进制位的奇数位和偶数位时,我们是指从右到左数的位置,本文给大家介绍了使... 目录一、问题描述二、解决思路三、函数实现四、宏实现五、总结一、问题描述使用C语言代码实现：将一个整
阅读更多...
C语言字符函数和字符串函数示例详解

C语言字符函数和字符串函数示例详解

《C语言字符函数和字符串函数示例详解》本文详细介绍了C语言中字符分类函数、字符转换函数及字符串操作函数的使用方法,并通过示例代码展示了如何实现这些功能,通过这些内容,读者可以深入理解并掌握C语言中的字... 目录一、字符分类函数二、字符转换函数三、strlen的使用和模拟实现3.1strlen函数3.2st
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2