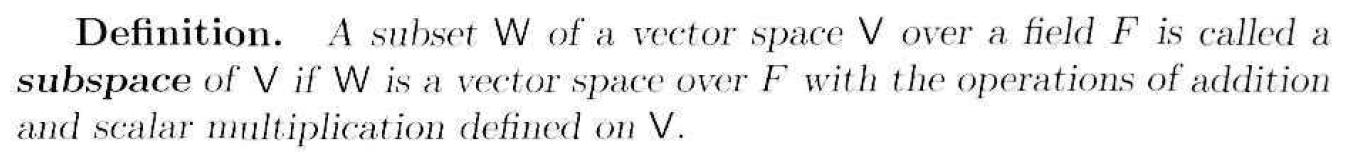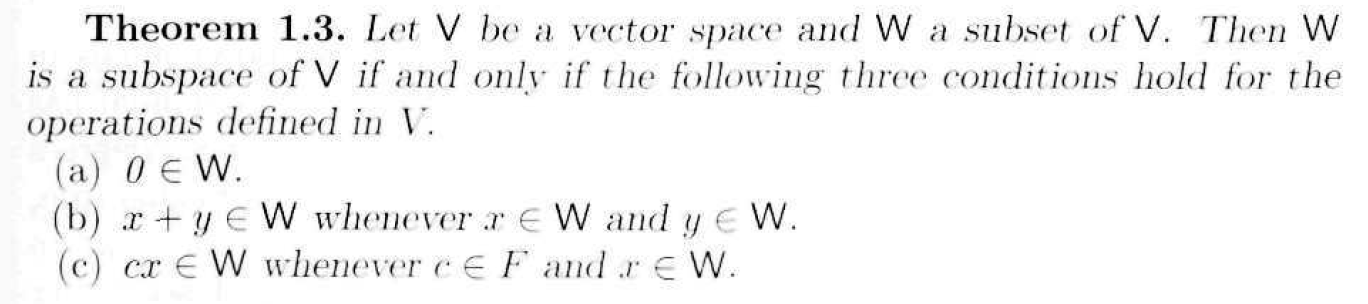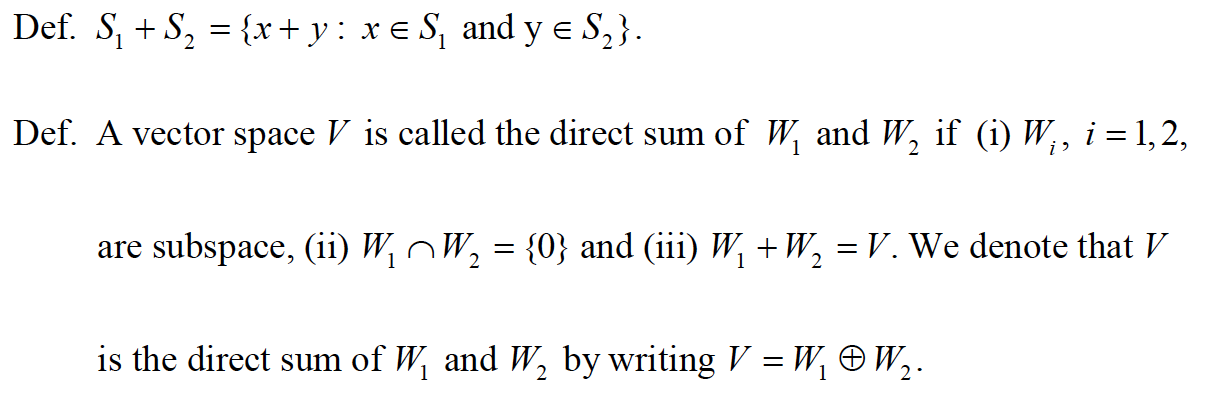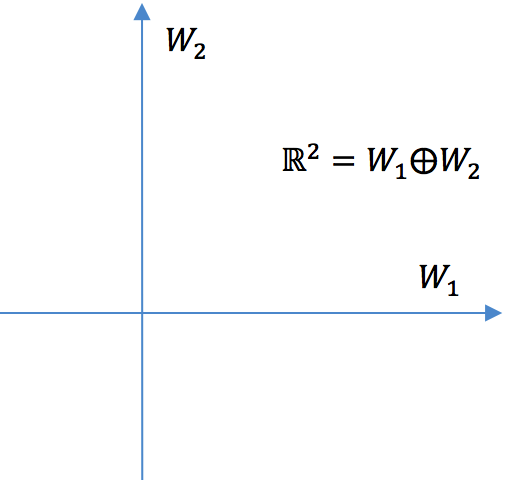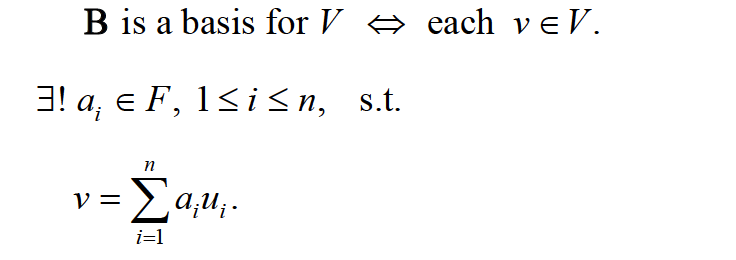线性代数笔记（1）：向量空间与子空间

一、向量空间的定义：

A vector space V over a field F consists of a set on which two operations (called addition and scalar multiplication) are defined, so that the following 10 properties hold.

（VS-1）x + y ∈ V，whenever x, y ∈ V. （加法封闭性）

（VS 0）ax ∈ V, whenever a ∈ F and x ∈ V. （乘法封闭性）

二、子空间的定义：

三、如何判断一个集合是子空间

四、与子空间有关的定理

Thm 1.4： 一个向量空间V的任意子空间之交集，仍然是V的子空间。

五、Direct Sum的概念

E.g.

六、Span的概念

不仅如此，我们还可以定义更广义的Span，此时向量空间中的一个元素将可以是更加泛化的对象（例如矩阵或多项式等）。

Thm 1.5：(i) Span(S) is a subspace of V；(ii) W is a subspace of V and S ⊂ W。Then Span(S) ⊂ W。i.e., Span(S) 是包含S的最小的子集空间。

七、线性独立与线性相关

定义：A subset S of a vector space V is called 线性相关，if ∃ distinct vectors u1, u2, …, un in S and scalars a1, a2, …, an not all 0, 使得

In this case, we also say that vectors of S are 线性相关（Any set S containing the 0 vector of 线性相关）。

一个集合是线性相关的，即是零向量可由集合中之向量非“trivial”的线性组合起来。或是说此集合有一个向量可用集合中其他向量线性组合起来，此处“trivial”是指组合系数皆为0。

八：基的概念

定义：A basis B for a vector space V is a 线性独立的 subset of V that generates V。

Thm 1.8：a vector space B = {u1, u2, …, un}, then

九：维度的概念

一个向量空间的基底的元素个数不一定是有限的，但下面的定理表明“如果这个向量空间可由一个有限集合所生成，则词此向量空间必有一个有限基底”。

Thm 1.9：Let V=Span(S)，where #(S)<∞. Then some subset of S is a basis for V.  Hence V has a finite basis.

如果一个向量空间有一个有限的基底，那么其它基底的元素个数是否相同呢？事实上我们可以证明：如果一个向量空间是由多个向量所张出的空间，则此向量空间不可能含有一个无限的线性独立集。更进一步，我们还可以得到：

由此我们可以来定义维度的概念：

1. A vector space, is called finite-dimensional if it has a finite basis.
2. The number of vectors in a basis is called the dimension of V and is denoted by dim(V).
3. A vector space that is not finite-dimensional is called infinite-dimensional.
   

最后我们还可以得出如下推论：If W is a subspace of a finite-dimensional vector space V, then any basis for W can be extended to a basis for V.

（本文完）

本文主要根据台湾交通大学开放课程线性代数（莊重 特聘教授主讲）之授课内容整理，并参考以下书籍：

【1】S.H. Friedberg, A.J. Insel, L.E Spence, 4th edition, Linear Algebra, Prentice-Hall, 2003

【2】David C. Lay. 刘深泉，等译. 线性代数及其应用（原书第3版），机械工业出版社，2005