Python 全栈体系【四阶】（四十三）

本文主要是介绍Python 全栈体系【四阶】（四十三），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第五章 深度学习

九、图像分割

3. 常用模型

3.4 DeepLab 系列

3.4.1 DeepLab v1(2015)

3.4.1.1 概述

图像分割和图像分类不一样，要对图像每个像素进行精确分类。在使用CNN对图像进行卷积、池化过程中，会导致特征图尺寸大幅度下降、分辨率降低，通过低分辨率特征图上采样生成原图的像素分类信息，容易导致信息丢失，分割边界不精确。DeepLab v1采用了空洞卷积、条件随机场等技术，有效提升了分割准确率。在 Pascal VOC 2012 的测试集 IOU 上达到了 71.6%，排名第一。速度方面，在GPU设备下推理可达每秒8帧。

3.4.1.2 空洞卷积

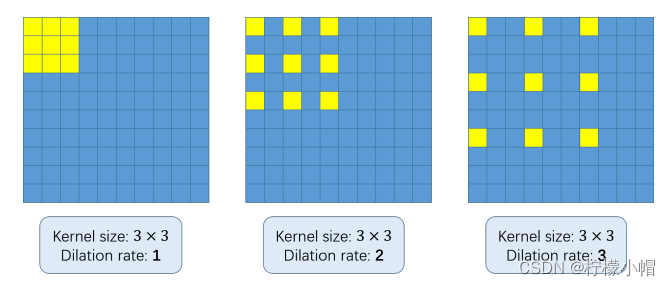
Dilated/Atrous Convolution(中文叫做空洞卷积或者膨胀卷积) ，是在标准的 convolution map 里注入空洞，以此来增加感受野。以下是一个空洞卷积示例图：

空洞卷积示例图

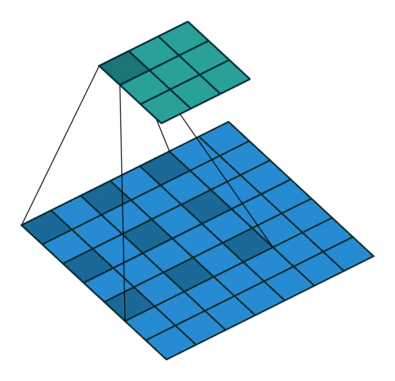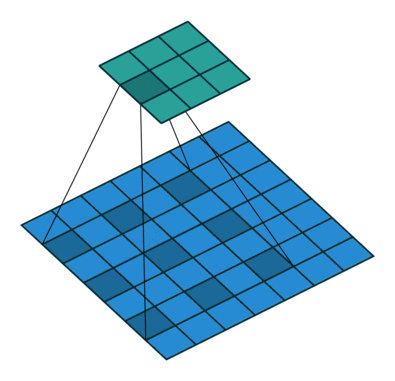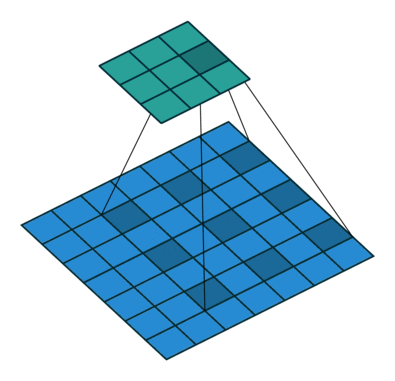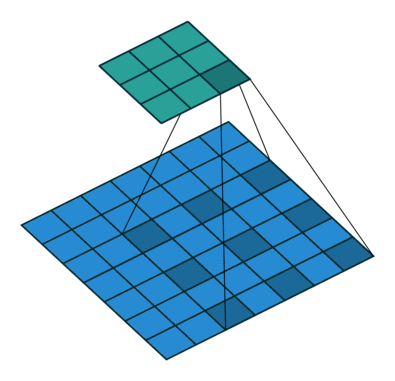
在空洞卷积中，通过添加空洞，在不增加参数、不进行降采样的情况下，增加感受野。空洞卷积有两种理解，一是可以理解为将卷积核扩展，如图卷积核为 3*3 但是这里将卷积核变为 5*5 即在卷积核每行每列中间加0。二是理解为在特征图上每隔1行或一列取数与 3*3 卷积核进行卷积。当不填充空洞时，dilation rate为1，当填充1时，dilation rate为2，当填充2时，dilation rate为3。如下图所示：

不同膨胀率的空洞卷积

空洞卷积最初的提出是为了解决图像分割的问题而提出的,常见的图像分割算法通常使用池化层和卷积层来增加感受野(Receptive Filed),同时也缩小了特征图尺寸(resolution),然后再利用上采样还原图像尺寸,特征图缩小再放大的过程造成了精度上的损失,因此需要一种操作可以在增加感受野的同时保持特征图的尺寸不变,从而代替下采样和上采样操作。

3.4.1.3 条件随机场

条件随机场（Conditional random field，CRF）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔可夫随机场。

马尔科夫随机场是具有马尔科夫特性的随机场。马尔科夫性质指的是一个随机变量序列按时间先后关系依次排开的时候，第N+1时刻的分布特性，与N时刻以前的随机变量的取值无关。拿天气来打个比方。如果我们假定天气是马尔可夫的，其意思就是我们假设今天的天气仅仅与昨天的天气存在概率上的关联，而与前天及前天以前的天气没有关系。其它如传染病和谣言的传播规律，就是具有马尔可夫性质的。

3.4.1.4 网络结构

DeepLab v1使用VGG-16作为基础模型，为了更适合图像分割任务，做出了以下修改：

• 将最后三个全连接层（fc6, fc7, fc8）改成卷积层
• 将最后两个池化层（pool4, pool5）步长由2改成1
• 将最后三个卷积层（conv5_1, conv5_2, conv5_3）的dilate rate 设置为2
• 输出层通道数改为21（20个类别，1个背景）

3.4.1.5 能量函数

条件随机场对分割边沿的改善效果

DeepLab v1使用了全连接条件随机场（Fully-connected Conditional Random Field）来保证分类准确和位置准确。其能量函数：

$$E(x)=\sum _i{\theta }_i(x_i)+\sum _{ij}{\theta }_{ij}(x_i,x_j)$$

训练的目标要最小化能量函数，函数第一项：

$${\theta }_i(x_i)=-logP(x_i)$$

第一项用来保证分类的准确率，其中$x_i$表示像素的标签值，$P(x_i)$表示DCNN的计算结果，准确率越高P(x)越接近1，该项值越小。函数第二项：

$$\begin{gathered} {\theta }_{ij}(x_i,x_j)=\mu (x_i,x_j)\sum _{m=1}^K{w}_m.k^m(f_i,f_j) \\ \mu (x_i,x_j)=1if{x}_i\ne x_j，otherwise0 \end{gathered}$$

其中，$\mu (x_i,x_j)$表示只考虑标签不相同的两个像素点，$k^m(f_i,f_j)$为一个高斯核函数，具体表示为：

$$w_{1}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\alpha }^2}-\frac{||I_i-I_j|{|}^2}{2{\sigma }_{\beta }^2})+w_{2}exp(-\frac{||p_i-p_j|{|}^2}{2{\sigma }_{\gamma }^2})$$

此函数主要由两个像素点的位置和颜色决定，位置为主、颜色为辅。该公式第一部分由位置（p表示）、颜色共同确定（I表示），第二项由位置确定，${\sigma }_{\alpha },{\sigma }_{\beta },{\sigma }_{\gamma }$控制高斯核的比例。

条件随机场边沿精修效果

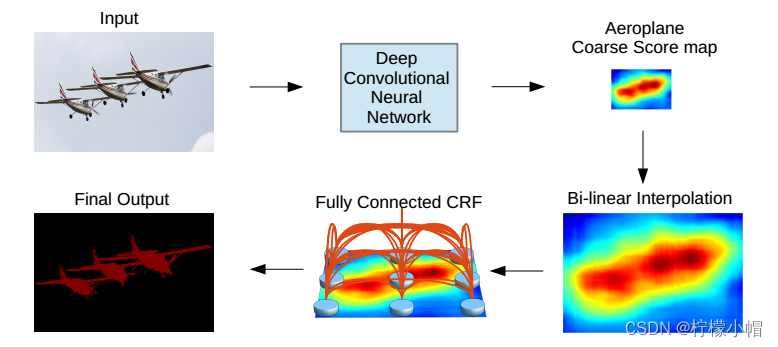
3.4.1.6 效果

• 自对比试验

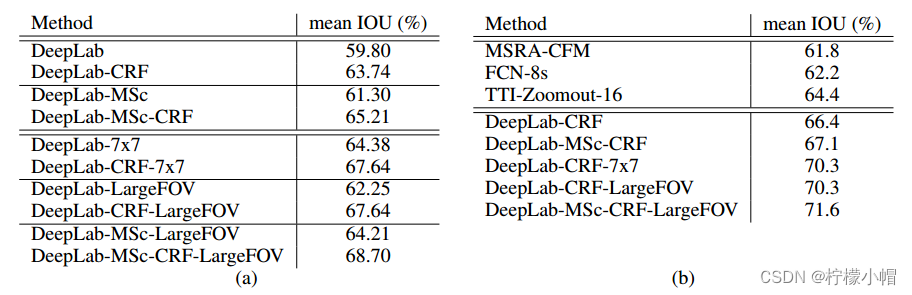
左表为采用不同策略下的IOU均值，其中，MSc表示多尺度融合，CRF表示条件随机场，LargFOV表大范围视野。右表为其它模型与该模型各种策略对比。

• 与FCN-8s和TTI-Zoomout-16的效果对比

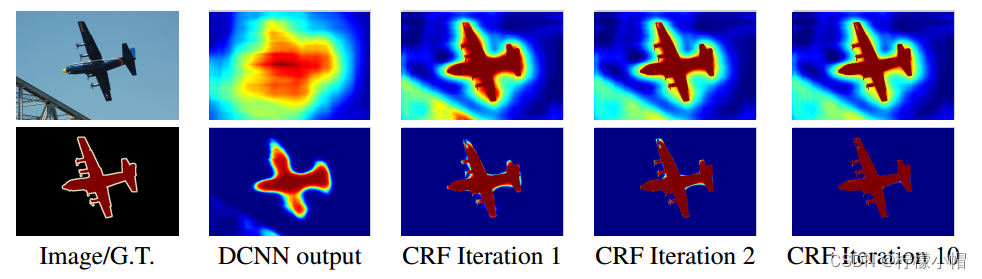
从上到下依次为原图、真实标记、被对比的模型分割效果、DeepLab-CRF分割效果。

3.4.2 DeepLab v2（2017）

DeepLab v2在DeepLab v1的基础上，主要引入了ASPP(Atrous Spatial Pyramid Pooling，膨胀空间金字塔池化)策略，在给定的输入上以不同采样率的空洞卷积并行采样，相当于以多个比例捕捉图像的上下文，从而获得更好的分割性能。ASPP原理如下图所示：

以下是PASCAL VOC 2012数据集上不同kernel size以及不同大小的膨胀率（atrous sampling rate）的实验对比：

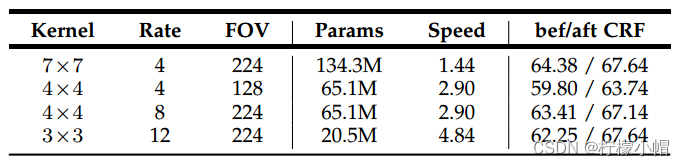
以下是PASCAL VOC 2012数据集上分割效果展示：

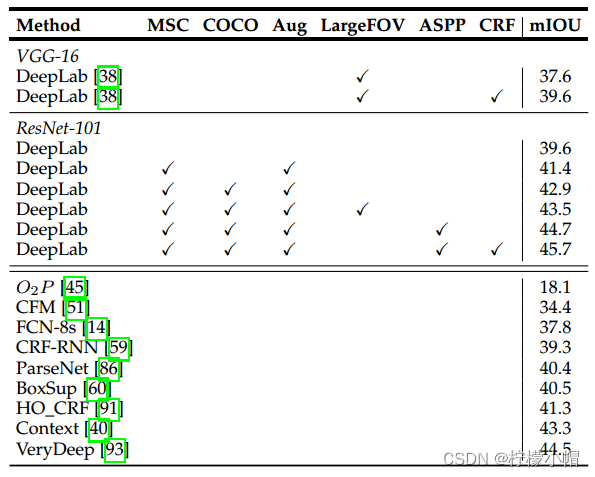
以下是使用ResNet-101在PASCAL VOC 2012数据集上的实验对比：

其中，MSC表示多尺度输入最大融合，COCO表示采用在MS-COCO上预训练的模型，Aug表示通过随机缩放增加数据。以下是跟其它模型的对比：

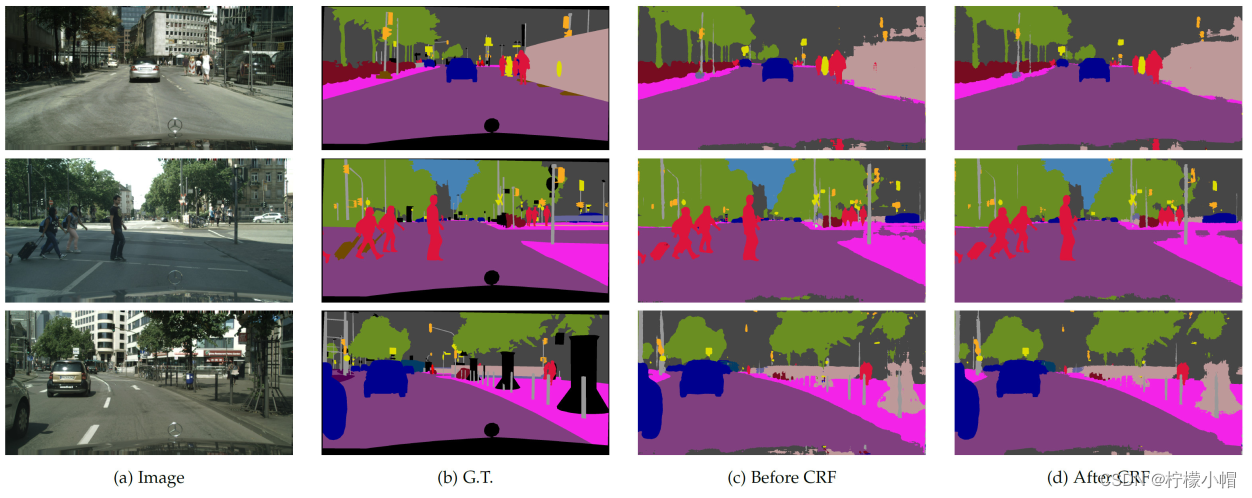
以下是在Cityscapes数据集上的分割效果：

以下是分割失败的示例：

这篇关于Python 全栈体系【四阶】（四十三）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---