本文主要是介绍算法设计与分析 例题 绘制Huffman树、循环赛、分治、最短路与动态规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.考虑用哈夫曼算法来找字符a,b,c,d,e,f 的最优编码。这些字符出现在文件中
的频数之比为 20:10:6:4:44:16。要求:
(1)(4 分)简述使用哈夫曼算法构造最优编码的基本步骤;
(2)(5 分)构造对应的哈夫曼树,并据此给出a,b,c,d,e,f 的一种最优编码。
解:1)、哈夫曼算法是构造最优编码树的贪心算法。其基本思想是,首先所
有字符对应n 棵树构成的森林,每棵树只有一个结点,根权为对应字符的频率。然后,重复
下列过程n-1 次:将森林中的根权最小的两棵树进行合并产生一个新树,该新树根的两个子
树分别是参与合并的两棵子树,根权为两个子树根权之和。
2)、根据题中数据构造哈夫曼树如下图所示。
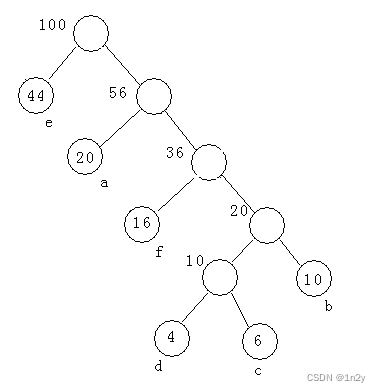
由此可以得出 a,b,c,d,e,f 的一组最优的编码:01,0000,00010,00011, 1,001。
2.
设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表:
每个选手必须与其他n-1名选手比赛各一次;每个选手一天至多只能赛一次;
循环赛要在最短时间内完成.
(1)(4分)循环赛最少需要进行( n-1 )天.
(2)(6分)当n=23=8时,请画出循环赛日程表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | 4 | 3 | 6 | 5 | 8 | 7 |
| 3 | 4 | 1 | 2 | 7 | 8 | 5 | 6 |
| 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 |
| 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| 6 | 5 | 8 | 7 | 2 | 1 | 4 | 3 |
| 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
3.
请用分治策略设计递归的归并排序算法,并分析其时间复杂性(要求:分别给出divide、conquer、combine这三个阶段所花的时间,并在此基础上列出递归方程,最后用套用公式法求出其解的渐进阶)。
答 : Template <class Type>
void MergeSort (Type a[ ], int left, int right)
{ if (left<right)
{ int i=(left+right)/2;
MergeSort(a, left, i);
MergeSort(a, i+1, right);
Merge(a, b, left, right);
Copy(a, b, left, right);
}
}
Divide 阶段的时间复杂性: O(1)
Conquer阶段的时间复杂性: 2T(n)
Combine阶段的时间复杂性: Θ(n) 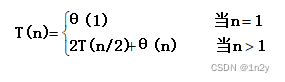
用套用公式法:a=2, b=2, nlog ba = n , f(n)=n, 因为f(n)与nlog ba 同阶,
∴T(n) =Θ(nlogn)
4.
对下图所示的连通网络G,用克鲁斯卡尔(Kruskal)算法求G的最小生成树T,请写出在算法执行过程中,依次加入T的边集TE中的边。说明该算法的贪心策略和算法的基本思想,并简要分析算法的时间复杂度。

TE={(3,4), (2,3),(1,5),(4,6)(4,5)}
贪心策略是每次都在连接两个不同连通分量的边中选权值最小的边。
基本思想:首先将图中所有顶点都放到生成树中,然后每次都在连接两个不同连通分量的边中选权值最小的边,将其放入生成树中,直到生成树中有n-1条边。
时间复杂度为:O(eloge)
5.
用动态规划策略求解最长公共子序列问题:
(1)给出计算最优值的递归方程。
(2)给定两个序列X={B,C,D,A},Y={A,B,C,B},请采用动态规划策略求出其最长公共子序列,要求给出过程。
(1)
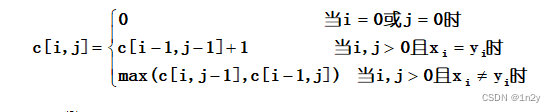
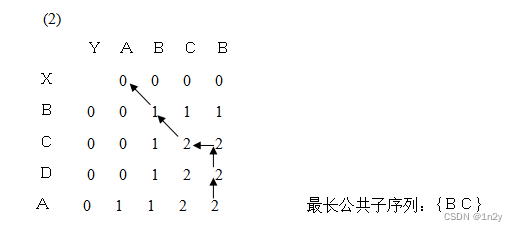
这篇关于算法设计与分析 例题 绘制Huffman树、循环赛、分治、最短路与动态规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







