MHD、MQA、GQA注意力机制详解

本文主要是介绍MHD、MQA、GQA注意力机制详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

MHD、MQA、GQA注意力机制详解

注意力机制详解及代码
- 前言：
- MHA
- MQA
- GQA

注意力机制详解及代码

前言：

自回归解码器推理是 Transformer 模型的一个严重瓶颈，因为在每个解码步骤中加载解码器权重以及所有注意键和值会产生内存带宽开销

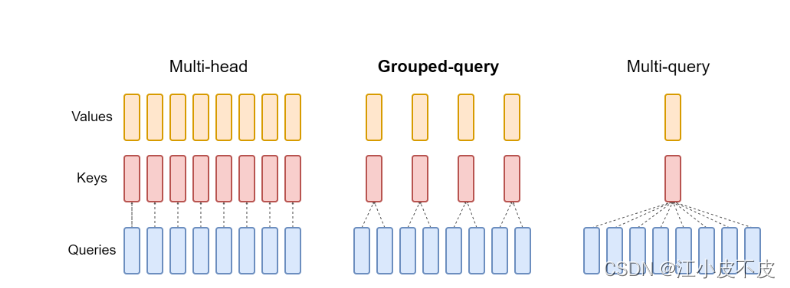
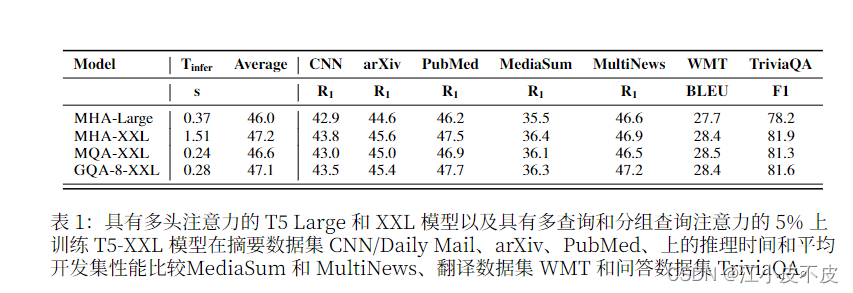
下图为三种注意力机制的结构图和实验结果

在这里插入图片描述

MHA

多头注意力机制是Transformer模型中的核心组件。在其设计中，"多头"意味着该机制并不只计算一种注意力权重，而是并行计算多种权重，每种权重都从不同的“视角”捕获输入的不同信息。

hidden_state经过线性层得到q、k、v
q、k、v经过split后增加一个维度：num_heads
q、k计算注意力分数score
softmax对注意力分数进行归一化得到注意力权重attention_probs
使用注意力权重和值计算输出：output
对注意力输出进行拼接concat

import torch
from torch import nn
class MutiHeadAttention(torch.nn.Module):def __init__(self, hidden_size, num_heads):super(MutiHeadAttention, self).__init__()self.num_heads = num_headsself.head_dim = hidden_size // num_heads## 初始化Q、K、V投影矩阵self.q_linear = nn.Linear(hidden_size, hidden_size)self.k_linear = nn.Linear(hidden_size, hidden_size)self.v_linear = nn.Linear(hidden_size, hidden_size)## 输出线性层self.o_linear = nn.Linear(hidden_size, hidden_size)def forward(self, hidden_state, attention_mask=None):batch_size = hidden_state.size()[0]query = self.q_linear(hidden_state)key = self.k_linear(hidden_state)value = self.v_linear(hidden_state)query = self.split_head(query)key = self.split_head(key)value = self.split_head(value)## 计算注意力分数attention_scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim))if attention_mask != None:attention_scores += attention_mask * -1e-9## 对注意力分数进行归一化attention_probs = torch.softmax(attention_scores, dim=-1)output = torch.matmul(attention_probs, value)## 对注意力输出进行拼接output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)output = self.o_linear(output)return outputdef split_head(self, x):batch_size = x.size()[0]return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1,2)

MQA

多查询注意力（MQA）可能导致质量下降和训练不稳定，并且训练针对质量和推理优化的单独模型可能不可行。此外，虽然一些语言模型已经使用了多查询注意力，如PaLM但许多语言模型没有，包括公开可用的语言模型，如T5和LLaM.

hidden_state经过线性层得到q、k、v
q、k、v经过split后增加一个维度：num_heads(q = num_heads,k=1,v=1)。相当于多个query，即多查询。
q、k计算注意力分数score
softmax对注意力分数进行归一化得到注意力权重attention_probs
使用注意力权重和值计算输出：output
对注意力输出进行拼接concat

## 多查询注意力
import torch
from torch import nn
class MutiQueryAttention(torch.nn.Module):def __init__(self, hidden_size, num_heads):super(MutiQueryAttention, self).__init__()self.num_heads = num_headsself.head_dim = hidden_size // num_heads## 初始化Q、K、V投影矩阵self.q_linear = nn.Linear(hidden_size, hidden_size)self.k_linear = nn.Linear(hidden_size, self.head_dim) ###self.v_linear = nn.Linear(hidden_size, self.head_dim) ##### 输出线性层self.o_linear = nn.Linear(hidden_size, hidden_size)def forward(self, hidden_state, attention_mask=None):batch_size = hidden_state.size()[0]query = self.q_linear(hidden_state)key = self.k_linear(hidden_state)value = self.v_linear(hidden_state)query = self.split_head(query)key = self.split_head(key, 1)value = self.split_head(value, 1)## 计算注意力分数attention_scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim))if attention_mask != None:attention_scores += attention_mask * -1e-9## 对注意力分数进行归一化attention_probs = torch.softmax(attention_scores, dim=-1)output = torch.matmul(attention_probs, value)output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)output = self.o_linear(output)return outputdef split_head(self, x, head_num=None):batch_size = x.size()[0]if head_num == None:return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1,2)else:return x.view(batch_size, -1, head_num, self.head_dim).transpose(1,2)

GQA

使用 5% 的原始预训练计算将现有的多头语言模型检查点训练到具有 MQA 的模型中
引入分组查询注意力 (GQA)，这是多头语言模型的泛化。查询注意力，它使用中间,多于一个，少于查询头数量的键值头。
经过训练的GQA 实现了接近多头注意力的质量，并且速度与 MQA 相当。

hidden_state经过线性层得到q、k、v
q、k、v经过split后增加一个维度：num_heads(q = num_heads,k=group_num,v=group_num)。相当于把多头分组了，比如原先有10个头，那就是10个query,分成5组，每组2个query,1个value,1个key。
q、k计算注意力分数score
softmax对注意力分数进行归一化得到注意力权重attention_probs
使用注意力权重和值计算输出：output
对注意力输出进行拼接concat

## 分组注意力查询
import torch
from torch import nn
class MutiGroupAttention(torch.nn.Module):def __init__(self, hidden_size, num_heads, group_num):super(MutiGroupAttention, self).__init__()self.num_heads = num_headsself.head_dim = hidden_size // num_headsself.group_num = group_num## 初始化Q、K、V投影矩阵self.q_linear = nn.Linear(hidden_size, hidden_size)self.k_linear = nn.Linear(hidden_size, self.group_num * self.head_dim)self.v_linear = nn.Linear(hidden_size, self.group_num * self.head_dim)## 输出线性层self.o_linear = nn.Linear(hidden_size, hidden_size)def forward(self, hidden_state, attention_mask=None):batch_size = hidden_state.size()[0]query = self.q_linear(hidden_state)key = self.k_linear(hidden_state)value = self.v_linear(hidden_state)query = self.split_head(query)key = self.split_head(key, self.group_num)value = self.split_head(value, self.group_num)## 计算注意力分数attention_scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim))if attention_mask != None:attention_scores += attention_mask * -1e-9## 对注意力分数进行归一化attention_probs = torch.softmax(attention_scores, dim=-1)output = torch.matmul(attention_probs, value)output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.head_dim * self.num_heads)output = self.o_linear(output)return outputdef split_head(self, x, group_num=None):batch_size,seq_len = x.size()[:2]if group_num == None:return x.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1,2)else:x = x.view(batch_size, -1, group_num, self.head_dim).transpose(1,2)x = x[:, :, None, :, :].expand(batch_size, group_num, self.num_heads // group_num, seq_len, self.head_dim).reshape(batch_size, self.num_heads // group_num * group_num, seq_len, self.head_dim)return x

这篇关于MHD、MQA、GQA注意力机制详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！