图形学基础笔记III：图形管线中的多边形裁剪算法、Sutherland-Hodgman、Guard Band Clipping

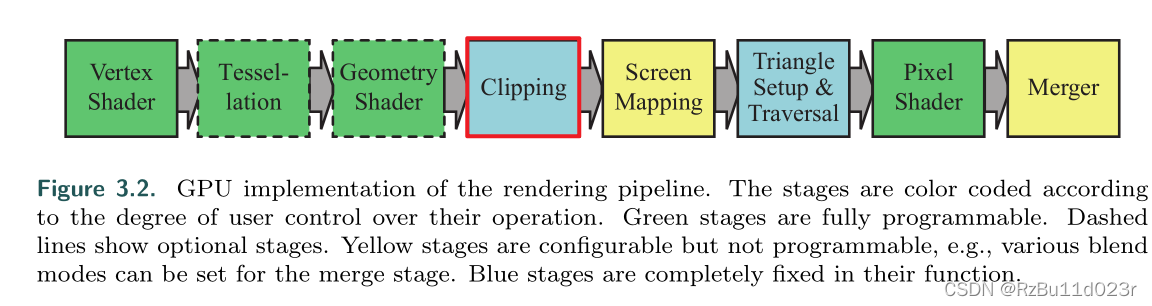
这个主要讲的是viewport 里的。

从 frustum （根据 fov 视场角 和 aspect ratio 纵横比决定 lrbt，front、near 是由摄像机距离和世界大小决定的）到 viewport 之后，能够看到的就只有投影后的 cuboid 在 viewport 里面的东西了。

问题是这个 clipping 是在 CPU 还是 GPU？实际有多个阶段，从 culling，CPU clipping 到 GPU clipping 和GPU rasterization。

本文尝试讲解这个问题，不过实际显卡和驱动变幻莫测，还需要更多参考资料。

但是有些麻烦的是因为只能处理三角形，如果裁剪了之后变成 polygon 了就要重新划分三角形了。好在三角形切一刀只会变成三角形或者四边形（quadrilateral）。

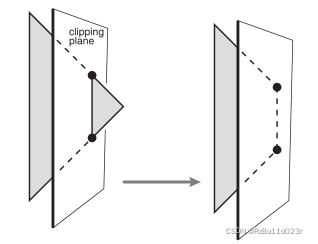
所以可以用下面的伪代码对整个 cuboid 内的 3D 三角形进行处理。

tiger book 也分析了裁剪实际放在 mvp 之前也可以，除以齐次坐标后也可以，在mvp之后也可以，但是除法之后（世界坐标）对于眼睛附近的地方是不连续的，所以这方面的运动就很难，所以一般在 MVP 后的除法之前做，而超平面也不难表示。对于 mvp 之后的平面方程则是最简单了（因为就是正立方体）。

首先是对直线的裁剪的硬件算法，即 cohen-sutherland 算法。对于多边形的裁剪是基于直线的裁剪的 sutherland-hodgman。一般讲解的是 2D 的情况，实际有 3D 的算法。

这部分算法可能是在 CPU 做的，也可能是在 GPU（看下面的 Guard band clipping 里面就明白了，对于不同的区域而言，有一些必须 CPU 就剪好，有一些可以让 GPU 剪，最后都是看你驱动怎么实现的），而且最新的硬件算法你也不知道是什么，会经过奇特的优化，其中还涉及到插值的问题。

对于一半在 viewport 里面的三角形，其实最简单的做法是 AABB 遍历的时候只访问 viewport 里面的像素就行了，感觉也没什么，关键是你不能剪掉的啊，剪掉了那 vertex 的信息就没了（OpenGL 规定是在 VS 后面进行 clipping），还要重建新的三角形和分割，那还 render 个寂寞。

对于 hardware clipping 来说，实际你还是要进行这部分的数据传输。如果不想数据传输就涉及在 CPU 端做 culling。optimization - At what phase in rendering does clipping occur? - Stack Overflow

当然，上面说的最简单的做法是 AABB 遍历的时候只访问 viewport 里面的像素就行。但是这样实际是要求显卡的实际能用的缓冲区是要大于 viewport 的。如果你的图元连缓冲区都放不下，是不是就一定要做类似 sutherland-hodgman 然后按老虎书说的要看情况拆成两个新的三角形，还要处理边界值（根据被剪掉的顶点插值好属性从而不会丢失）。

Nvidia 和 D3D 有一个叫 guard band clipping 的 culling + clipping 的层次算法，从 CPU 一路到 GPU 的，所以可能 GPU 就没有实现：

Guard Band Clipping in Direct3D (nvidia.cn)

Cohen-Sutherland

• 平面编码：使用 tbrl 4位编码，如果是在 viewport 的 tbrl 就为 1. 每个位置最多两个 1.
• 

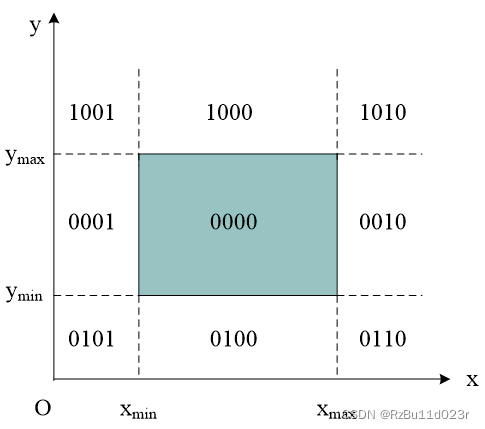
• 在交点处把线段分为两段。其中一段完全在窗口外，可弃之。然后对另一段重复上述处理。

• 
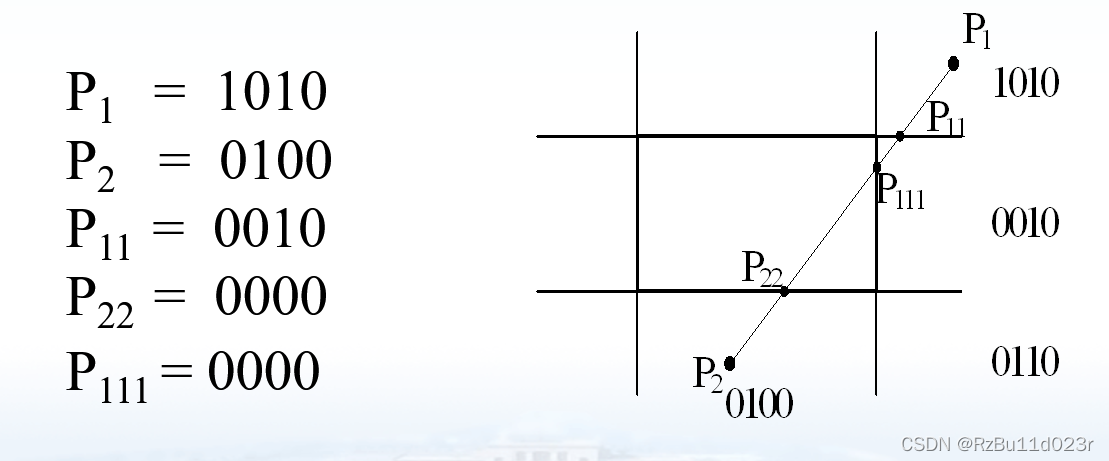
• 如上图，实际只需要对直线的端点（其实一直说直线说的是线段）求这个编码，根据不同的情况，然后递归/迭代进行下去：

	// Cohen–Sutherland clipping algorithm clips a line from// P0 = (x0, y0) to P1 = (x1, y1) against a rectangle with// diagonal from (xmin, ymin) to (xmax, ymax).void CohenSutherlandLineClipAndDraw(double x0,double y0,double x1,double y1) {// compute outcodes for P0, P1, and whatever point lies outside the clip// rectangleOutCode outcode0 = ComputeOutCode(x0, y0);OutCode outcode1 = ComputeOutCode(x1, y1);bool accept = false;while (true) {if (!(outcode0 | outcode1)) {// bitwise OR is 0: both points inside window; trivially accept and exit// loopaccept = true, break;} else if (outcode0 & outcode1) {// bitwise AND is not 0: both points share an outside zone (LEFT, RIGHT,// TOP, or BOTTOM), so both must be outside window; exit loop (accept is// false)break;} else {// failed both tests, so calculate the line segment to clip// from an outside point to an intersection with clip edgedouble x, y;// At least one endpoint is outside the clip rectangle; pick it.OutCode outcodeOut = outcode1 > outcode0 ? outcode1 : outcode0;// Now find the intersection point;// use formulas://   slope = (y1 - y0) / (x1 - x0)//   x = x0 + (1 / slope) * (ym - y0), where ym is ymin or ymax//   y = y0 + slope * (xm - x0), where xm is xmin or xmax// No need to worry about divide-by-zero because, in each case, the// outcode bit being tested guarantees the denominator is non-zeroif (outcodeOut & TOP)  // point is above the clip windowx = x0 + (x1 - x0) * (ymax - y0) / (y1 - y0), y = ymax;else if (outcodeOut & BOTTOM)  // point is below the clip windowx = x0 + (x1 - x0) * (ymin - y0) / (y1 - y0), y = ymin;else if (outcodeOut & RIGHT)  // point is to the right of clip windowy = y0 + (y1 - y0) * (xmax - x0) / (x1 - x0), x = xmax;else if (outcodeOut & LEFT)  // point is to the left of clip windowy = y0 + (y1 - y0) * (xmin - x0) / (x1 - x0), x = xmin;// Now we move outside point to intersection point to clip// and get ready for next pass.if (outcodeOut == outcode0)x0 = x, y0 = y, outcode0 = ComputeOutCode(x0, y0);elsex1 = x, y1 = y, outcode1 = ComputeOutCode(x1, y1);}}
}

Sutherland-Hodgman 多边形裁剪算法

• 关键在于怎么确定凸的凹的那些要不要封闭。
• 按某个顺序逐边裁剪：

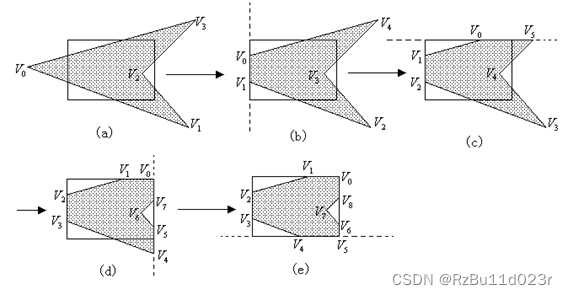
• 多边形边的分类：把所有边都按逆时针确定起点 S 和终点 P。每次裁剪的时候，viewport 边界裁剪线要做延长，再划分 in out 分区

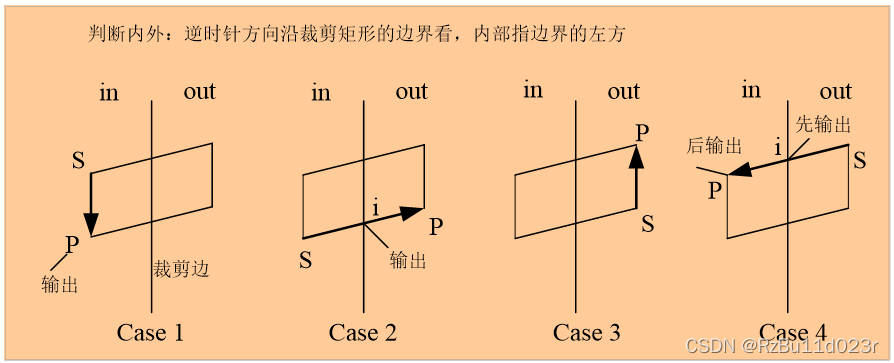
• case1 是整条边都在viewport 里面的（通过 Cohen-Sutherland 得知的），只保留终点。
• case2 是内往外出，保留交点。（起点会由另一个闭合边输出），交点的求法可以用数值解。
• case3 边在外面，不保留顶点。
• case4 外面进来，保留交点和终点。
• 一言：对于相交的，在 viewport 内的终点，以及交点都要保留

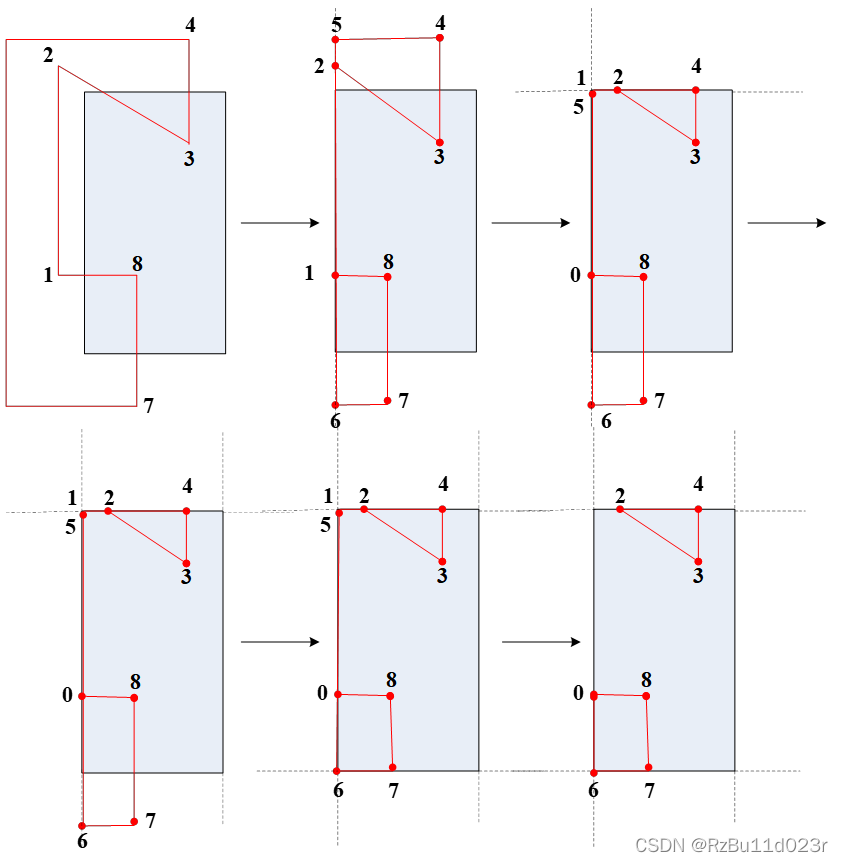
• 后处理：由于这个算法输出的是点，这里演示了一个凹多边形，所以你怎么把连连起来呢？wiki 说 Note that if the subject polygon was concave at vertices outside the clipping polygon, the new polygon may have coincident (i.e., overlapping) edges – this is acceptable for rendering, but not for other applications such as computing shadows.
• 所以说必须要做一个后处理，实际你处理不了，只能加一些专家系统的解决一部分问题。不过既然三角形是凸的，所以实际可以不管他（然而我感觉用这个只处理三角形是不是有点浪费？）别的算法也是针对 polygon 的。可能说三角形还能优化。不过注意的是，对于三角形切了之后变成四边形的情况还要割呢。
• 交点插值：由于与切割线的交点已经不是原来三角形的顶点了，所以 clipping 的过程要求一下新的顶点的重心坐标，把插值后的属性放到新的顶点上取。
• 切分三角形：这个过程很简单的，只要切完了之后看一下有多少个顶点，如果是 4 个就切一刀，把对应 vertex 的 attributes 都要复制一份。
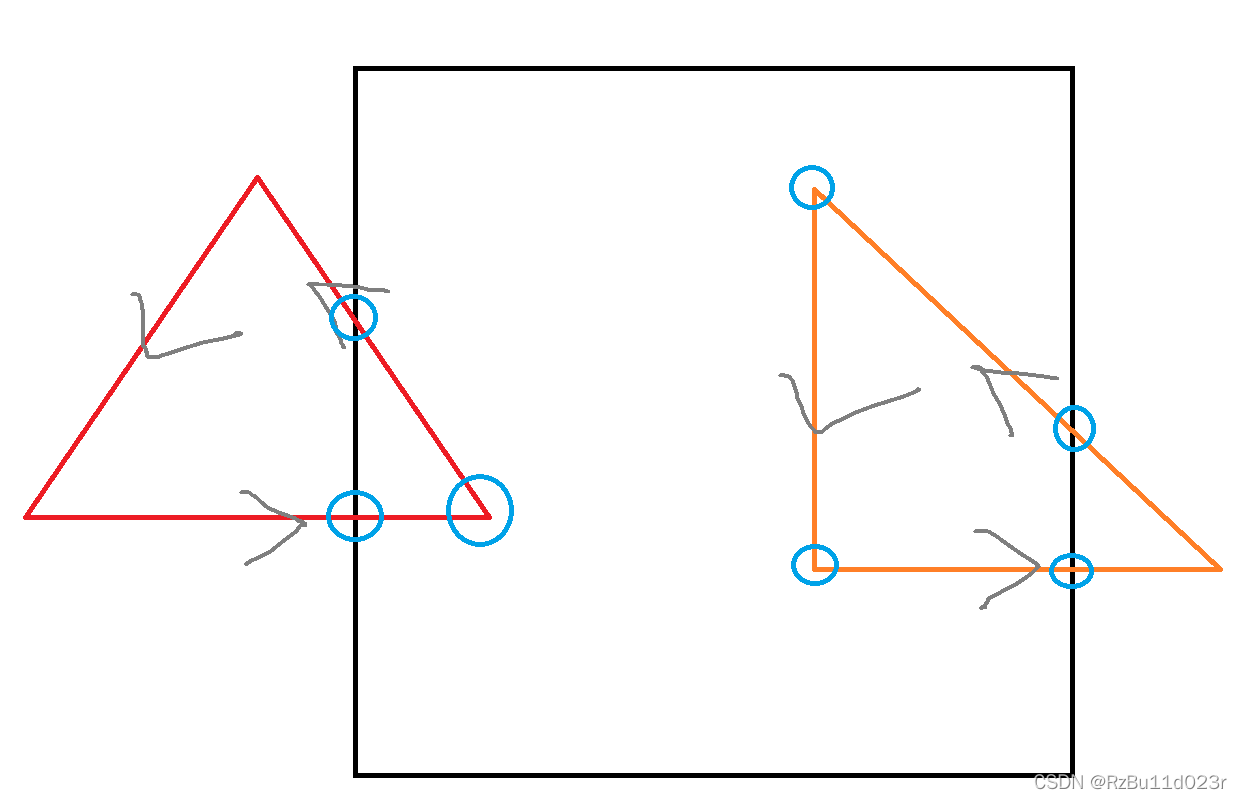
• 原理：其实上边这些操作指南一样的东西，是可以用三角形来推导出来的。规定顺时针方向和逆时针方向都行。就是依次遍历三角形的三条边，然后能够依次把要保留（裁剪）的顶点不遗漏不多选地列举出来。其实那几条规则对三角形来说实在是想当然的，可以穷举所有情况，。

Homogeneous Clipping

• 算法论文：p245-blinn.pdf (fabiensanglard.net)
• 上面这个 Sutherland-Hodgman 算法一看好像只能用在 2D 上，有一定的局限。
• 但是我们可以考虑把裁剪线扩展为裁剪面，而交点还是交点，只不过变成了 3D 的直线（线段）与平面的交点。
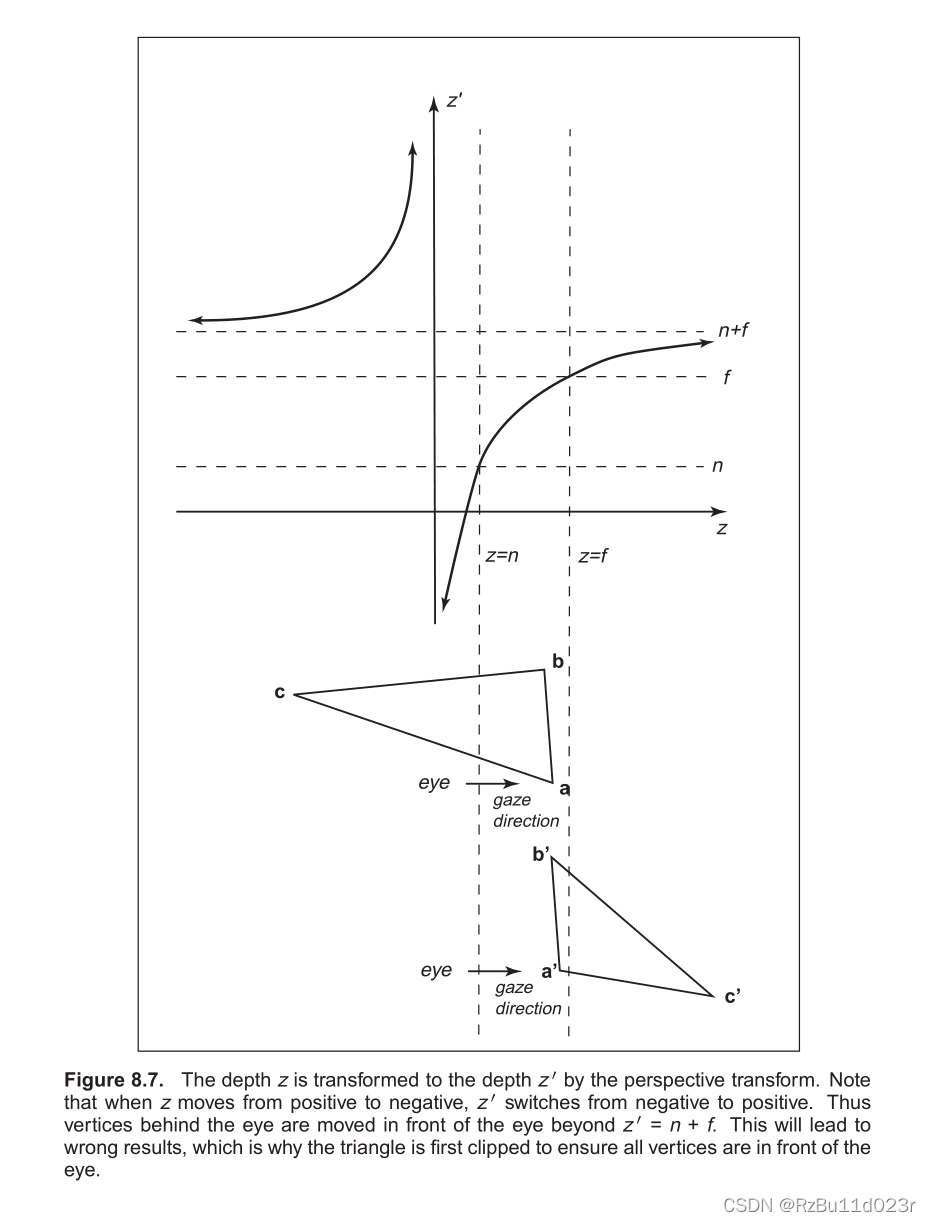
• 前面提到虎书说到，我们可以在 MVP 之后，做除法之前进行 clipping。这就是齐次坐标裁剪。复习一下为什么要在除法之前进行 clipping 呢，这是因为除法之后（世界坐标）对于眼睛附近的地方是不连续的（复习 MVP 矩阵的推导），所以一般在除法之前做。（记住除法的那个 w 其实在运算过程为了化简其他，用的就是 z 就行了，也就是因为这个 z 的除法引入了反比例函数）。

• P 矩阵的问题就是这里，回想 games101 讲 transformation II 的矩阵的推导，由于 P 矩阵主要是我们基于 x 和 y 来推导的，z 的这个是凑出来的。所以这下问题就导致最后会出错

• 但是实际还是大部分可以是正比关系的，只要 n + f 够给力，但是反比例函数的特性，必然有一部分会被弄反。

• 实际疯狂 google 找到齐次裁剪的关键字之后，也发现了有大佬的漂亮公式文章，这里也附上作为参考，我暂时就不研究具体公式（不过其实和上面 Sutherland-Hodgman 算法的差不多）。计算机图形学补充2：齐次空间裁剪(Homogeneous Space Clipping) - 知乎 (zhihu.com)。需要注意齐次坐标裁剪和 Sutherland-Hodgman 的关系就行。

实际显卡驱动中的 culling & clipping

• Nvidia 的算法说明：Guard Band Clipping in Direct3D (nvidia.cn)
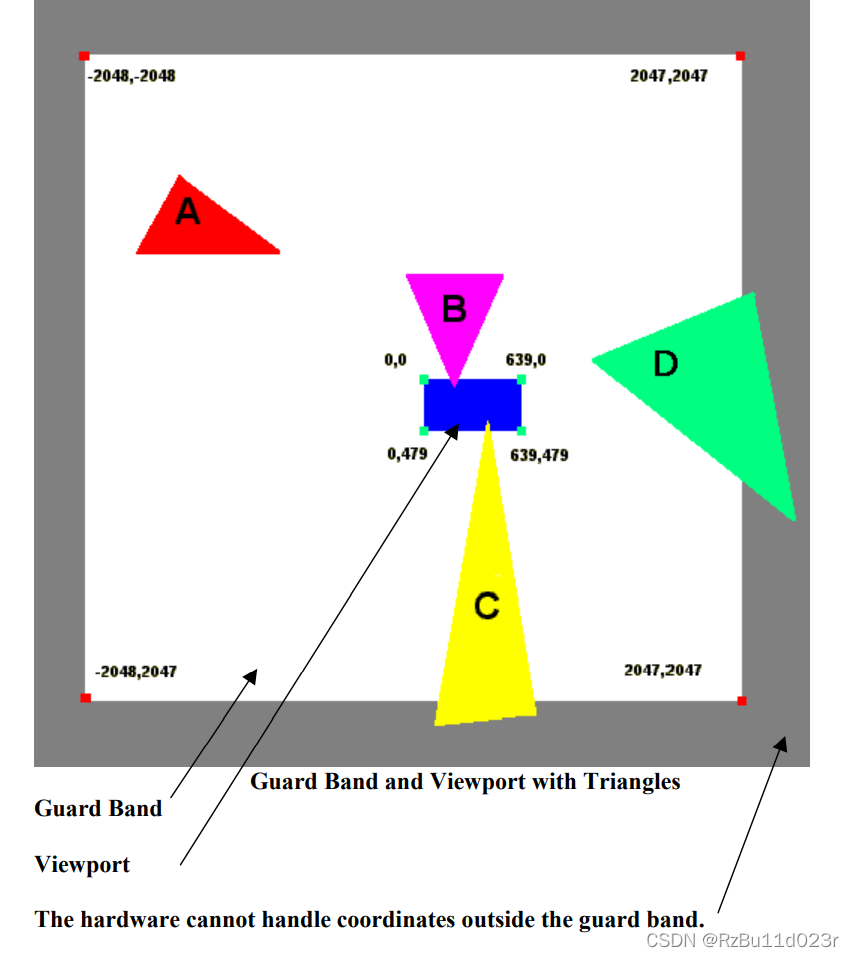
• 由于显卡的帧缓冲是有限的，为了能够支持更大的世界，实际显卡的帧缓冲是支持比 viewport 的帧缓冲大小大得多的的，这个叫做guard band。但是他仍然是有限的，显卡能够处理的三角形也是必须在有限的空间里的（但是三角形的个数可以轻松上亿甚至十几亿），一半 60 帧的引擎同屏渲染几亿三角形应该不在话下。
• 所以实际 CPU 传给 GPU 进行光栅化的三角形空间位置也不能超出视口太多然后还要渲染的，这样的结果是显卡自己处理不了这种三角形，因为他无法访问这么大范围的数据。

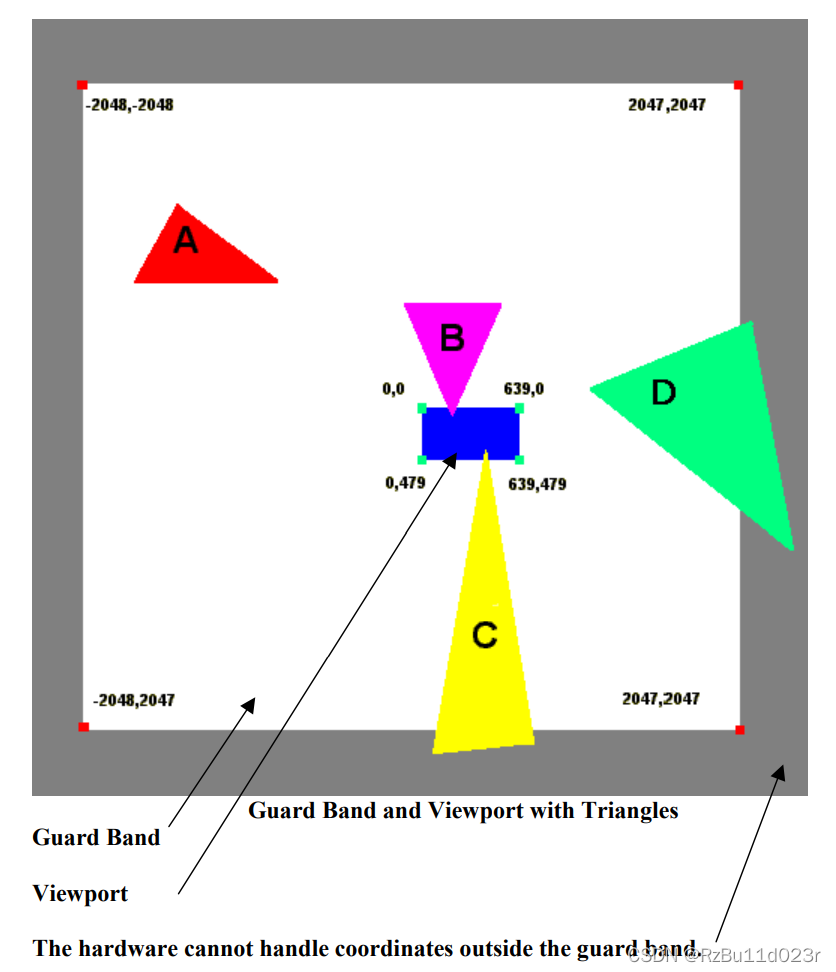
• 所以是两阶段裁剪算法：CPU 必须保证所有传送的三角形都在 Guard band 里面。GPU 自己再裁一遍。
• 上图，A 可以硬件丢弃，B 可以硬件裁剪。D 传送的时候就被丢掉了（驱动做），或者 CPU 可以丢掉。C 就是一个很麻烦的三角形，关键是他还和 viewport 相交了。所以必须要进行软件裁剪（CPU 进行）。

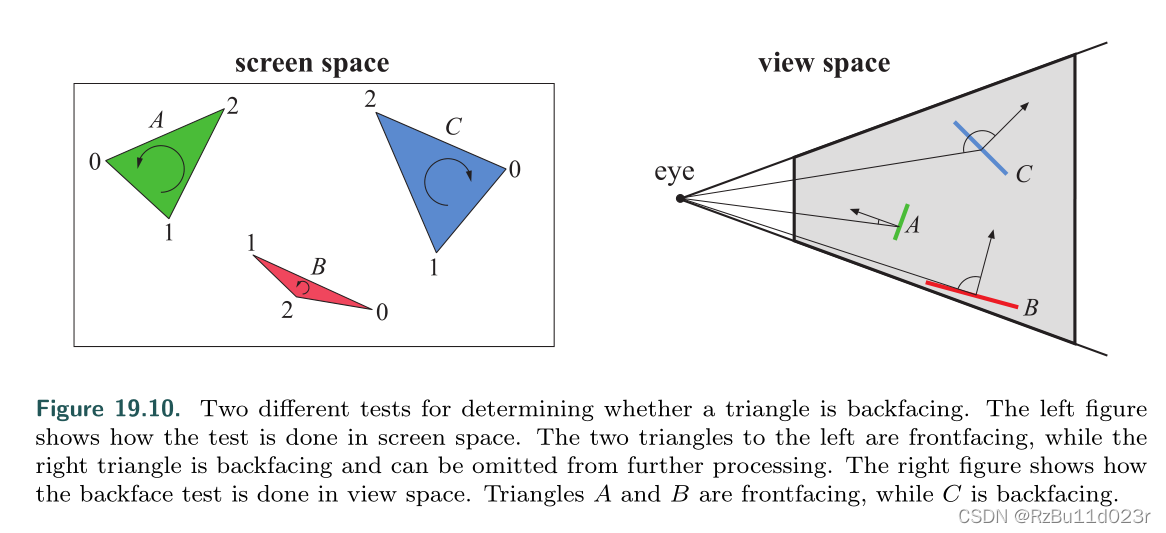
实际对于3D 来说，一些背面三角形没有必要渲染，直接丢掉，这个叫做背向面剔除