本文主要是介绍图形学基础笔记I:直线和圆的光栅算法、中点线算法、中点圆算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
实际现代显卡支持的图元就只有点、线、三角形。这是基于这样的事实:
实际对于 3D 来说肯定全是基于三角形的 geometry - OpenGL: Is it more efficient to use GL_QUADS or GL_TRIANGLES? - Stack Overflow,显卡也全部用重心坐标和 AABB 来填充三角形的。
三角形线框模式和非三角形线框模式(GUI、CAD),也很容易实现,使用 bresenham 中点算法就行了。
点就更简单了,如果没有涉及抗锯齿直接取整写显存就行了。
整理一下就是说:
- 线框模式各种形状:应用的话比如 CAD,GUI,不管什么多边形,什么样子都能用 bresenham 画线给你画出来。对于圆的话也是用 bresenham(midpoint)。
- 实体填充各种形状:由于屏幕像素是离散的,所以三角形足够拟合各种形状,只需要 AABB 重心填充算法。
所以直线算法还是必要的。对于圆的画,如果搞 GUI 的话可能需要。
DDA digital differential analyzer
- 一个很自然的算法
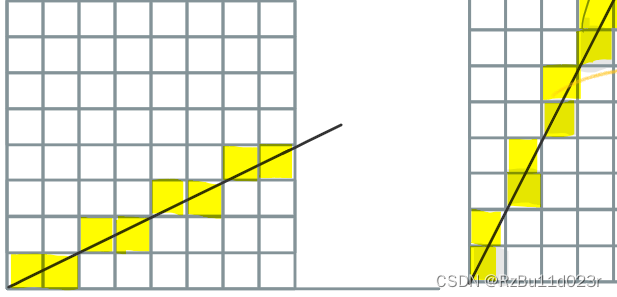
- 描述:把直线和网格线的交点找出来,然后浮点转成整数就确定落在网格上的点了。
- 要点:在于要么 x 方向总是整数要么 y 方向总是整数。保证方式通过让变化最大方向上的增量为 1.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #include <stdlib.h> #include <math.h> inline int round(const float a) { return int(a + 0.5); } void lineDDA(int x0, int y0, int xEnd, int yEnd) { int dx = xEnd - x0, dy = yEnd - y0, steps, k; float xIncrement, yIncrement, x = x0, y = y0; if (fabs(dx) > fabs(dy)) steps = fabs(dx); else steps = fabs(dy); xIncrement = float(dx) / float(steps); yIncrement = float(dy) / float(steps); setPixel(round(x), round(y)); for (k = 0; k < steps; k++) { x += xIncrement; y += yIncrement; setPixel(round(x), round(y)); } } |
中点线算法 Mid Point
- 改进点:浮点运算
- 整数判别表达式:由于网格线中点是可以直接表达的,构建一个表达式来判断中点是否在直线上。
- 应付考试为什么不能理解现场推公式:因为他有不显然的推导过程。。。
- 增量表达式:通过在公式时域上构建递推公式实现增量计算。
- 要点:由于横轴网格中点和纵轴网格中点的表达式不一样,导致不同斜率的增量表达式不一样,必须用 if else 写两套代码。
Bresenham 算法
- 这个和中点算法是同构的,画出来的点也是一目一样的。
- 不过他相对于中点线多了个 2倍避免小数。但是根据一些参考资料好像根本不会出现普通的中点线也不会出现小数?存疑,实际一般都用 bresenham 就行了。
- 四种情况,考虑斜率正的时候 x++ y++,表达式 d 两种,斜率负的时候 x++,y-- 表达式同样两种。不过至于 y 是+还是-其实可以算出来。为了统一,分为 x++,y?? 和 x??,y++ 的情况比较好写(表达式基本对称)。
- 代码是 cv wikipedia 的,现场推可以推出来,做不到。


中点圆算法
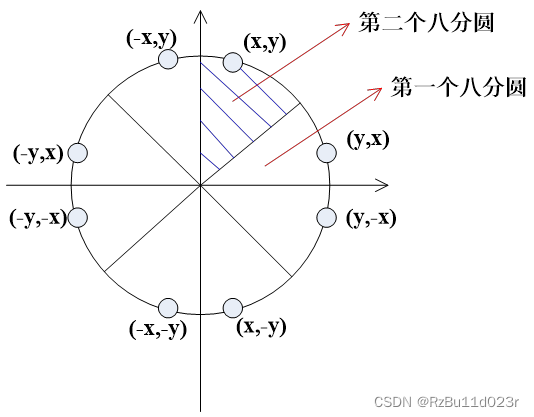
下面以第二个八分圆进行分析,最后再利用对称完成画圆。

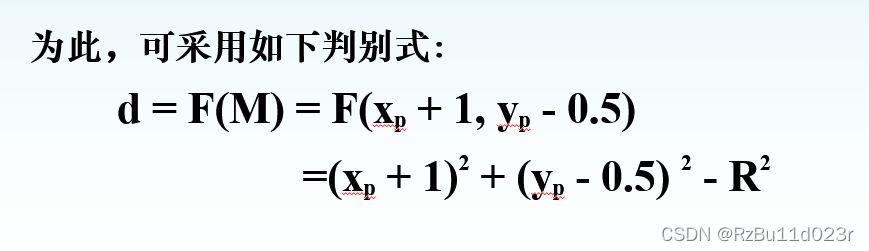



然后进行一些取整操作,比如 0.25 有没有都一样,所以可以去掉的。改写成代码就是这样:
第一个八分圆的

第二个八分圆的

这里比较基础。就这么简略了,起码有代码是完备的内容,足够实现参考了。
这篇关于图形学基础笔记I:直线和圆的光栅算法、中点线算法、中点圆算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





