本文主要是介绍神经网络如何学习到加法等算法 - 神经编码器-解释器(Neural Programmer-Interpreters),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
算法的本质
何为算法(algorithm)?
从狭义来讲,算法是计算机科学里面的概念,简单来说,所谓算法就是定义良好的计算过程,它取一个或者一组值作为输入,并产生出一个或一组值作为输出。亦即,算法就是一系列的计算步骤,用来将输入数据转换成输出结果[1]。
从广义来讲,算法是从初始态到可达目标态的序列过程。
如:命令机器人拿起一个瓶子,那么算法就是从机器手中没有瓶子到不断修正自己机器手到拿起一个瓶子的动作过程。而这些动作和程序没有本质的区别,都是序列化过程。假如我们将拿起瓶子的动作简化为基本的形式:Left,Right,Top,Down,Forward,Backward,OpenHand,CloseHand,这些动作的参数都为T,即持续时间,且简单的做匀速运动。那么机器人拿起瓶子这样的动作过程就可以概括为这些动作的组合序列过程,我们如果定义整个组合序列过程集合即机器人动作空间,那么这个算法就是找到这样一个或者多个子动作空间使机器人拿起瓶子。
神经编码器-解释器
本质上算法程序就是序列过程,但是通常算法程序都是人类写的。因为人工智能的发展,机器变得越来越智能,越来越能做很多事情,所以这里就有一个有趣的问题:如果机器能够学会了写出自己的算法并改变自身的算法,那么机器是否就拥有了自我进化的能力?
我们知道任何复杂的事物或概念C都必然由比他自己更简单的事物或概念S构成,如果S不能再分解为比自己更简单的东西,那么S就是C的一个因子,如果C=S那么C不能被分解。以自然数为例:0,1,2,3...任何自然数(排除0以外)必然可以由一个或者多个素数相乘得到,而素数无法被分解为除自身与1相乘的任何自然数相乘的形式,所以任何素数构成得到任何自然数(排除0以外)的乘法因子。同理,加法中任意个0与1可以相加构成任何的自然数,所以0与1构成任意自然数的加法因子。
由上,为了学习C我们可以先学习S,同样可以递归的找到学习C的所有因子。这和人类相似,我们学习概念也是从简单的开始,然后学习由简单概念构成的复杂概念,尤其在数学上,如果基本的自然数加减乘除都不会的话,自然无法学会更高级的线性方程。这也是我们常说的基础很重要的原因,因为复杂的东西由基础的东西构成。这个在自然语言中也呈现出简单到抽象的层次结构。
神经编码器-解释器(Neural Programmer-Interpreters,NPI)的思想和上面的类似,即我们可以先学习简单的算法,如:自然数加法,文本替换等,然后学习复杂的算法。在神经编码器-解释器之前,就有很多论文阐述如何学习加法的机器学习算法,如:神经图灵机(Neural Turing Machine),等等,还有最近Facebook发表的用强化学习来训练机器学习简单算法。
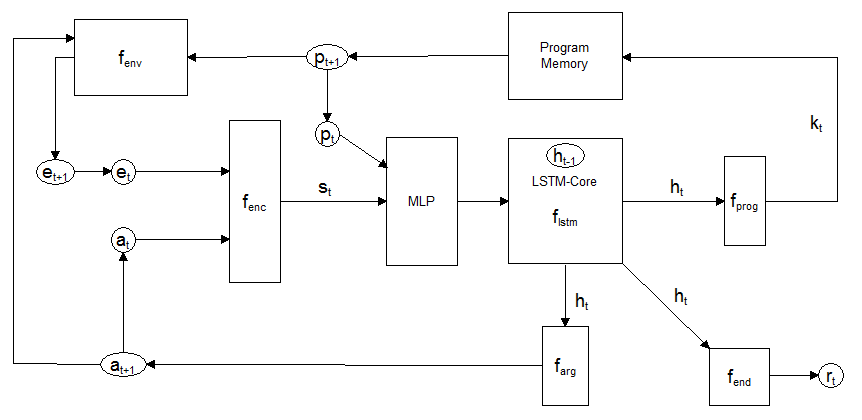
下面根据论文来叙述该算法的思想。NPI由三个可学习组件,即:一个任务未知的递归核心,一个持久的键值对程序内存和特定领域的编码器组成。其中该论文中的递归核心是以LSTM为基础的序列模型。下面是架构图:
前馈过程
其中:
为时间
的原始环境状态,
为函数参数,
为编码后的状态,
为特定领域的编码器(函数),
为程序或程序动作,
为LSTM的内部隐藏状态,
输出状态,
为多层感知机(MLP)和LSTM-Core构成的递归网络函数
为是否终止程序的概率,
为嵌入程序的键(key),
为下一个时间的参数值,
,
,
皆为解码器
为下一时间的环境状态,
只是环境变化函数,
并不是我们计算得到的,而是环境生成的。
加法计算过程
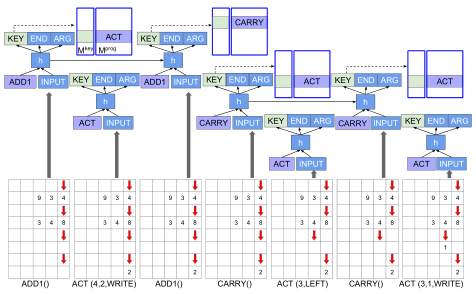
加法计算过程如下图:

整个加法是在一个表格中进行,其中第1,3,5,7行为指针可达位置,其他行为数字行,红色的箭头为指针,红色的箭头只能左右移动即:LEFT,RIGHT,而这些移动即我们的子程序,ADD,ACT...也是子程序或者叫因子程序。而指针指向的位置为他下面的格子。上面过程为第一个执行ADD1,产生下一个程序WRITE和两个参数,即位置为第4个指针行的指针所指位置(即第8行,第5列,下同)及得到的值2;然后执行并产生程序ADD1等等,都差不多不细讲。其中CARRY为进位程序,ACT是一个综合简化程序,WRITE为写入数字到表格。当然还有其他程序过程,这里只列举了加法。
训练
训练主要通过运行的轨迹即:这个时间步的输入和应该的输出
来监督式训练。最优参数通过下面的公式获得:
而代价函数为:
其中单步条件概率可以因子化为以下的和:
通过梯度上升法,求解最优参数集。 其他问题可参考[2]。
总结
有人说自然数加法很简单,实际上对于研究人工智能的人而言未必是简单的,因为我们不仅仅要知道是什么,更要知道为什么,往往简单的东西是难以说清楚的比如:1+1为什么等于2,很难说清楚,当然这是皮亚诺公理的内容。自然数加法的基础公理是大学数学分析才学的,相对的自然数加法则是小学数学的内容,所以what和why的层次有巨大的区别。在人工智能中自然数加法如果用回归逼近的方法来做只能得到近似解,而不能得到精确解,这个是有很大差别的。
参考:
1. Thomas H.Cormen、Charles E.Leiserson、etc,Introduction to Algorithms
2. Scott Reed 、Nando de Freitas,Neural Programmer-Interpreters
3. Neural Programmer-Interpreters 动画演示
这篇关于神经网络如何学习到加法等算法 - 神经编码器-解释器(Neural Programmer-Interpreters)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!