本文主要是介绍通过Matlab实现Hermite基函数进行信号拟合,可应用于信号降噪,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
利用Hermite基函数的Hermite近似,在不牺牲精度的情况下,实现对时序信号的降噪,文中图片以心电信号QRS波群滤除高频干扰为例。
1.知识背景
Hermite正交多项式是一类重要的正交多项式,它们起源于数学中的Hermite函数和特殊函数理论,它们在物理学、工程学和数学中都有广泛的应用。
Hermite正交多项式满足一组特殊的正交性质,即在一定的权函数下,它们彼此正交。在通常的情况下,这个权函数是e^(-x^2),即高斯权函数。这种正交性质使得Hermite多项式在傅立叶变换、量子力学、概率论等领域有着重要的应用。
Hermite正交多项式的一大特点是其递归关系。设Hn(x)表示Hermite多项式的第n阶多项式,则有如下递归关系:
Hermite正交多项式是通过递归关系定义的,下面是前六个Hermite正交多项式的表达式:
Hermite基函数是以Hermite多项式为基础构建的一组函数集合,通常用于函数逼近和信号处理等领域,Hermite基函数的形式如下:
其中,表示第n个Hermite基函数,
是对应的第n个Hermite多项式。Hermite基函数的特点是它们在实数轴上有限且彼此正交,因此在信号处理领域常用于构建正交基函数系列,用于信号分解滤波和重建等任务。
σ为30时,Hermite基函数图像如下所示(本文取前六个基函数对信号进行降噪):

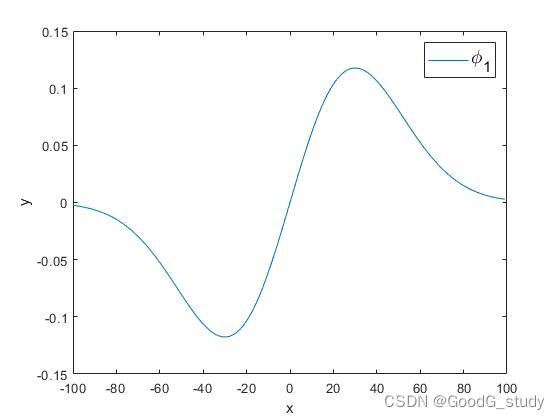
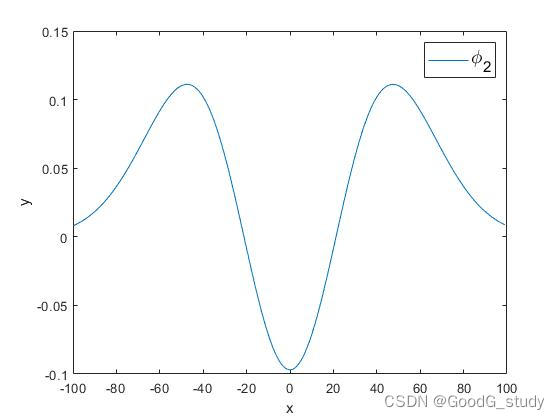
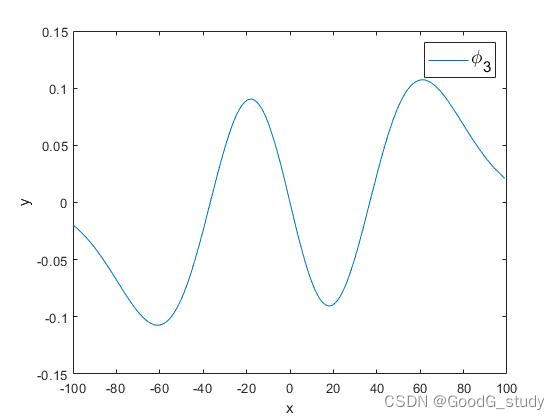
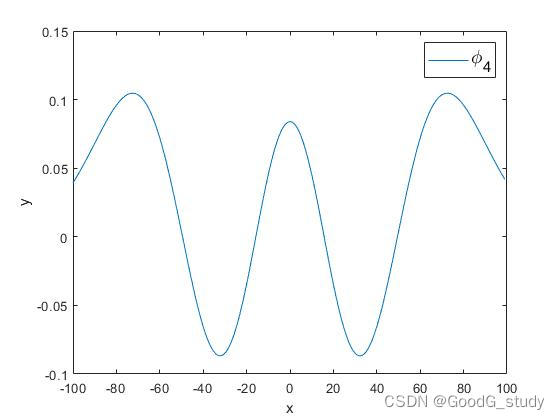
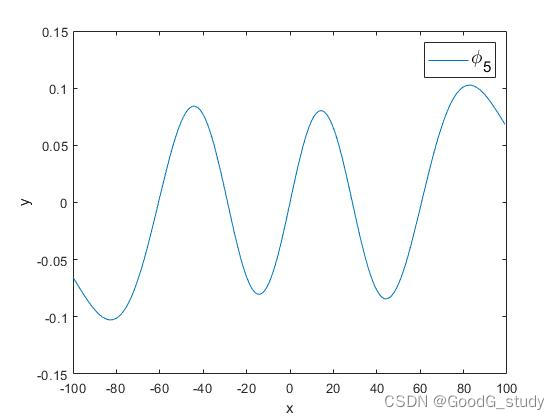
2.最终拟合
通过Hermite基函数对信号进行拟合实现降噪,拟合公式如下:
其中,表示拟合后的信号,
表示Hermite基函数的系数权重,不同的σ对应不同的权重,对于给定的σ,系数
计算公式如下:
最佳权重的选择根据均方误差(Mean Squared Error,MSE)的最小值进行选取,MSE公式如下:
其中表示拟合前的信号。
拟合效果如下图所示:
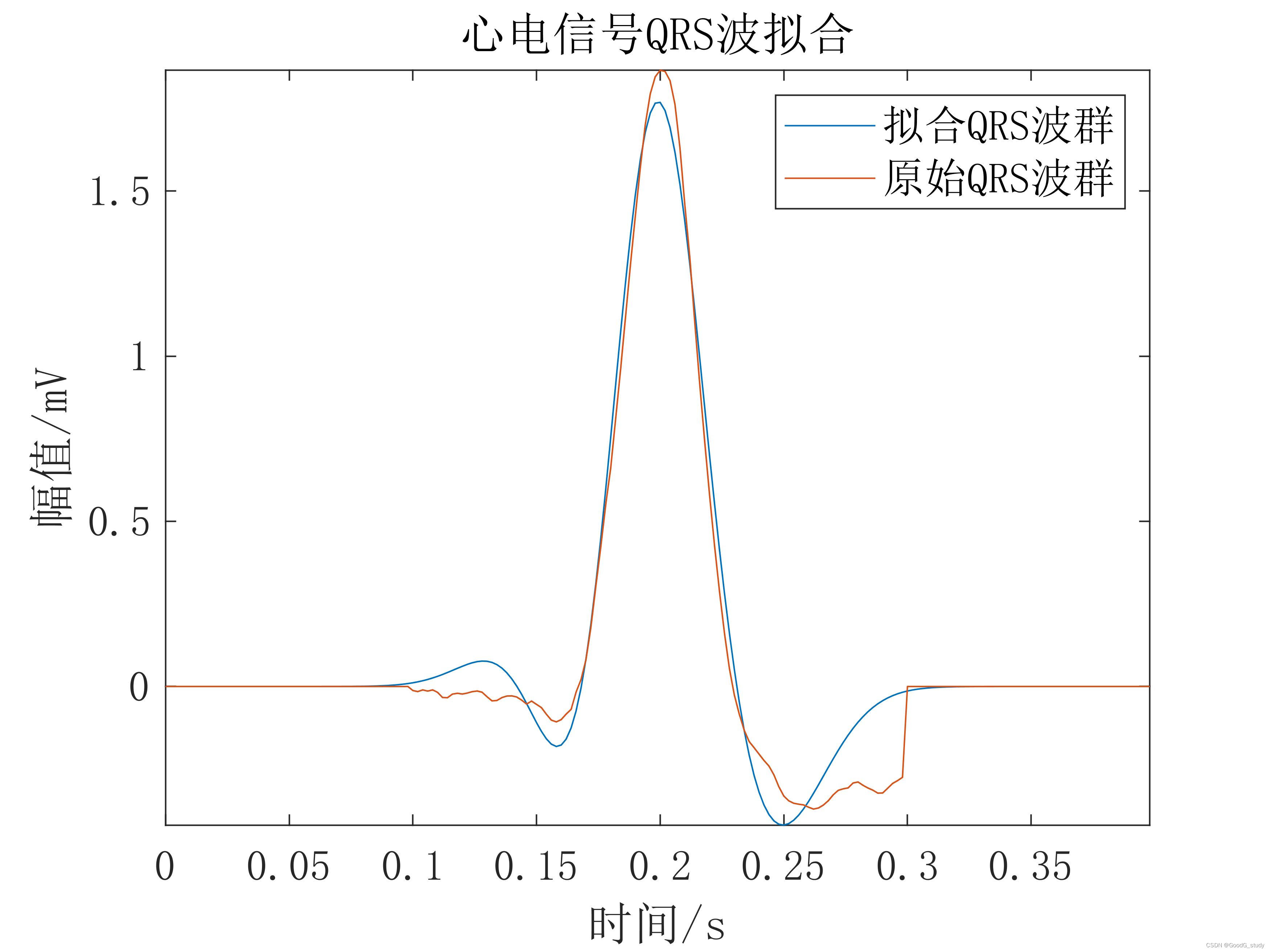
3.应用
该方法可应用于心电信号QRS波群滤除高频干扰,同理可应用于其他时序信号的滤波。
如需代码,请加下方微信:

这篇关于通过Matlab实现Hermite基函数进行信号拟合,可应用于信号降噪的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





