本文主要是介绍LeetCode-网络延迟时间(Dijkstra算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
每日一题
今天刷到一道有关的图的题,需要求单源最短路径,因此使用Dijkstra算法。
题目要求
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
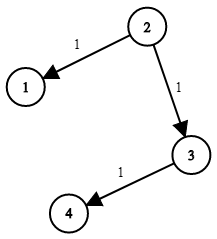
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 输出:2
示例 2:
输入:times = [[1,2,1]], n = 2, k = 1 输出:1
示例 3:
输入:times = [[1,2,1]], n = 2, k = 2 输出:-1
题目解析
题目中给了几个节点,并且给了节点之间的距离,要求我们从指定的某个节点发送信号。需要多久所有节点可以收到,这个明显要求从某个节点到所有节点的最短距离,因此可以采用Dijkstra。
Dijkstra算法
Dijkstra算法是一种用于解决单源最短路径问题的经典算法,由荷兰计算机科学家艾兹赫尔·迪科斯彻(Edsger W. Dijkstra)于1956年提出。该算法可以在加权图中找到从起始节点到所有其他节点的最短路径。
算法思想
-
初始化:将起始节点的距离设为0,其他节点的距离设为无穷大(或一个很大的值),并将所有节点标记为未访问。
-
遍历节点:从起始节点开始,依次遍历所有节点。
-
更新距离:对于当前节点的所有邻居节点,计算从起始节点经过当前节点到达邻居节点的距离。如果经过当前节点到达邻居节点的距离小于目前已知的最短距离,则更新邻居节点的距离值为经过当前节点到达邻居节点的距离,并标记当前节点为邻居节点的前驱节点。
-
选择下一个节点:从所有未访问的节点中选择距离起始节点最近的节点作为下一个当前节点,并标记该节点为已访问。
-
重复步骤3和4,直到所有节点都被访问过,或者目标节点的距离值被确定。
算法特点
- Dijkstra算法适用于没有负权边的加权有向图或无向图。
- 算法保证了在每一步选择当前最短路径的节点,因此得到的结果是最优解。
- 算法的时间复杂度为O(V^2),其中V是图中节点的数量。如果使用优先队列(如最小堆)来存储和选择距离最近的节点,时间复杂度可以优化到O(E + VlogV),其中E是图中边的数量。
图解流程如下:
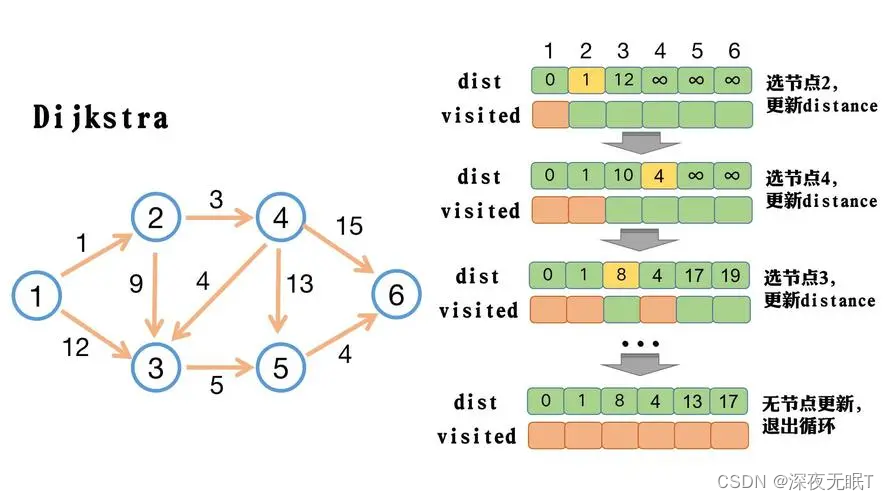
使用此算法需要两个数组,一个dist数组用来记录第k个节点到所有的节点最短距离,一个visited数组记录某个节点是否被访问过。
那么针对于这道题来说,我们一共需要创建三个数组
一个二维graph[i][j]数组,用来记录当前记录下的从i到j的距离
一个dist数组,记录第k个节点到所有的节点最短距离
一个used数组记录某个节点是否被访问过。
首先先将graph数组初始化,将距离全部设为最大。随后遍历给的times数组,记录下已经给出的节点间的距离。随后同步到dist数组中。
随后开始循环n-1次,在循环中嵌套循环,找到所有未访问节点中距离k最近的节点‘u’并记录下来已经访问过了。如果循环完毕后发现从k到不了某个未节点,则直接返回-1.最后再次进入一次循环,循环中对于节点j来说,判断是直接从k到j的距离小还是从可先到u再到j的距离小,因为我们刚得到了从k到u的最短距离,找到谁最小,赋值给dist[j].
最后经过多次循环,从k到所有节点的距离就存储在了dist中了,找到其中的最大的值就是我们要的答案。
代码实现
class Solution {public int networkDelayTime(int[][] times, int n, int k) {final int INF = Integer.MAX_VALUE / 2;int[][] graph = new int[n][n];boolean[] used = new boolean[n];int[] dist = new int[n];Arrays.fill(dist, INF);for (int i = 0; i < n; i++) {Arrays.fill(graph[i], INF);}for (int[] time : times) {graph[time[0] - 1][time[1] - 1] = time[2];}for (int i = 0; i < n; i++) { dist[i] = graph[k - 1][i];}dist[k - 1] = 0;used[k - 1] = true;for (int i = 0; i < n - 1; i++) {int min = INF;int u = -1;for (int j = 0; j < n; j++) {if (!used[j] && dist[j] < min) {min = dist[j];u = j;}}if (u == -1) {return -1;}used[u] = true;for (int j = 0; j < n; j++) {if (!used[j] && graph[u][j] + dist[u] < dist[j]) {dist[j] = graph[u][j] + dist[u];}}}int ans = 0;for (int i = 0; i < n; i++) {ans = Math.max(ans, dist[i]);}return ans == INF ? -1 : ans;}
}这篇关于LeetCode-网络延迟时间(Dijkstra算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





