虚树详解

本文主要是介绍虚树详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

虚树大意：通过建一棵只包含询问点和不超过询问点数减一个lca的树来减少点的个数，降低时间复杂度

这东西不难，常用于辅助树形dp，难点在于dp…
使用该算法的标志为不确定组的询问次数与给出的询问点数和 例如：
每次询问w个数，${\sum }_{i=1}^q{w}_i=300000$

---

算法：

构建过程十分简单，放心食用
举个例子：P2495 [SDOI2011]消耗战
就是找一些边割掉使得根与所有选定点不连通，使割掉的边权和最小
首先给出一棵树：（原谅我丑陋的图）

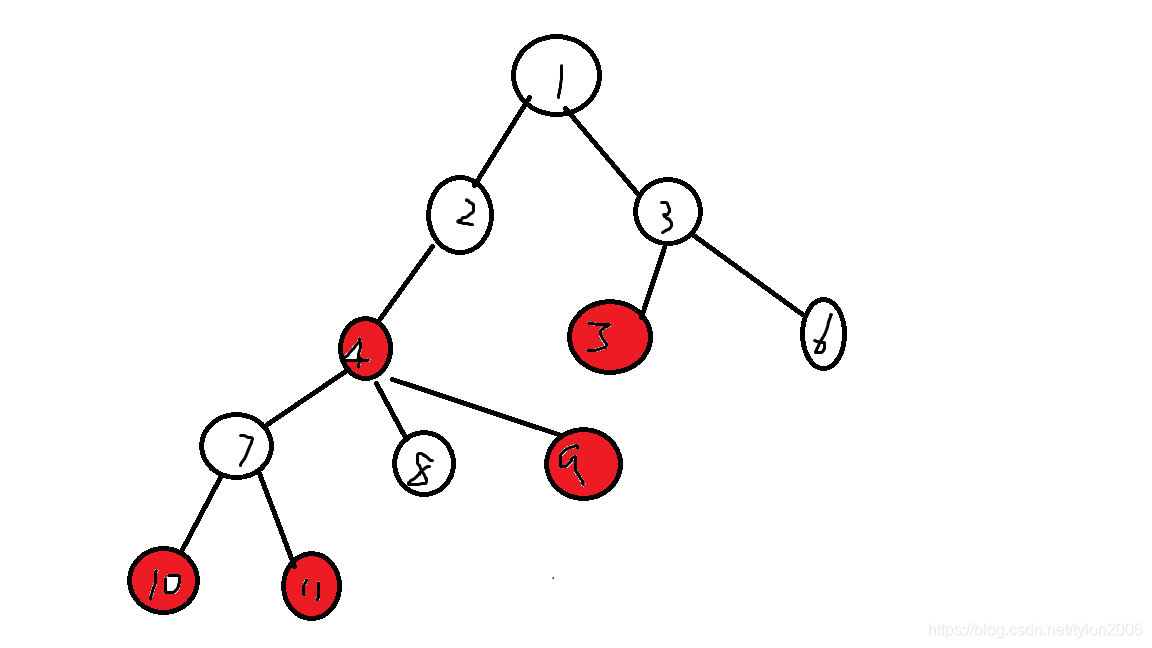
红色的点是我们要询问的，明显我们不可能直接在原树上搞O(n)dp，我要是全部点都选不就gg了。。
所以我们考虑省掉一些点来优化总点数。

很容易观察到，3和7号节点并没有对答案造成贡献，如果只是找最小边权只需要用一个前缀记录就可以，那么如何优化呢？

明显我们需要保证虚树仍保持节点深度关系的同时保证不加入无用点。对选定点按照dfn排序再依次插入，用栈记录当前的一条链，那么可见我们新加入一个点x会有以下两种情况：

1. 栈顶是x的祖先，直接加进去
2. 栈顶不是x的祖先，求栈顶和x的lca，不停出栈,并连一条stk[top-1]->stk[top]的边（构建当前链），直到找到栈内最后一个点的dfn>=lca的dfn，即栈顶上一个点的dfn<lca的dfn。如果栈顶的点不是lca，则连一条lca到栈顶的边，再把栈顶改成lca，加入x，保持深度递增。

其实我们的虚树的深度就是当前根到x路径上的选定点个数，加入lca是因为要使得同一深度的点保持这种关系。举个栗子，x和y的深度都是4，你连x->y或者y->x都会改变原树形态，此时就要lca->x，lca->y。
我们又按照了dfn排序，此时选定点有序，只需要处理相邻两点之间的位置问题即可。

注意一下，第一个点永远置为1，方便搜索；最后将栈内的全部出栈加边。

可以通过上面的图理解：

首先点排序后长这样：4 10 11 9 5

1. stk：1 (初始)
2. stk：1 4 此时加入了4，栈顶1是4的祖先
3. stk：1 4 10 同上
4. stk：1 4 7 11 此时加入11，11和栈顶10的祖ca是7，而4的深度小于七，那么把栈顶改为7，加入11
5. stk：1 4 9 此时加入9，9和栈顶11的lca是4，将11和7出栈，此时栈顶就是lca，无需改动，加入9
6. stk：1 5 此时加入5，5和栈顶9的lca是1，将4和9出栈，此时栈顶就是lca，无需改动，加入5
7. stk：1 此时将栈内元素出完

现在看看建出的树：
1 无
2 无
3 无
4 7->10
5 7->11 4->7
6 4->9 1->4
7 1->5

画出来长这样 ：

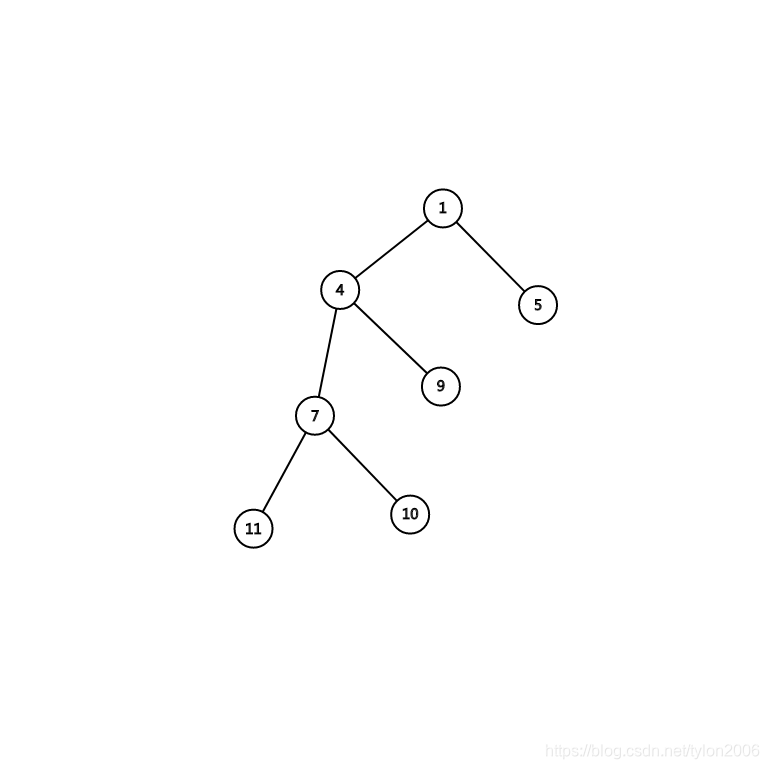
少了一堆点，效率up

时间复杂度分析：

刚才讲了只需要处理相邻两点的lca，即加入不超过w-1（w是询问点数）个lca。
那么每次询问只需要加入不超过2w-1个点。

总时间复杂度为$O({\sum }_{i=1}^q{w}_i\times logn)$，于是就可以快乐地解决问题了。

---

技巧：

建完虚树清除图是个问题，毕竟也不可能memset，瞬间上天。。。
我们可以dfs一边，每到一个点就清除其head，就不需要耗费过多时间。

还有一种方法，是类似迭代实现，就不需要建边。我们在建树过程中其实就是在遍历虚树，那么我们只要把加边操作替换为更新父节点信息，出栈时更新ans或者直接输出一号节点信息（看题目）即可。

---

代码：

我是用树剖求lca的。

#include<bits/stdc++.h>
using namespace std;
int dfn[250010],dep[250010],siz[250010],n,q;
int top[250010],fa[250010],stk[250010],son[250010],tot,tp;
int e[500010],w[500010],nxt[500010],head[250010],cnt;
int a[250010];
void add(int x,int y,int z){cnt++;e[cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}
void dfs1(int x,int f){fa[x]=f;siz[x]=1;dfn[x]=++tot;for(int i=head[x];i;i=nxt[i])if(e[i]!=f){int y=e[i];dep[y]=dep[x]+1;dfs1(y,x);siz[x]+=siz[y];if(siz[y]>siz[son[x]])son[x]=y;}
}
void dfs2(int x,int t){top[x]=t;if(son[x]==0) return;else dfs2(son[x],t);for(int i=head[x];i;i=nxt[i])if(top[e[i]]==0) dfs2(e[i],e[i]);
}
int lca(int x,int y){while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]]) swap(x,y);x=fa[top[x]];}if(dep[x]>dep[y]) swap(x,y);return x;
}
void add1(int x,int y){//根据题目自行填充 
}
void ins(int x){if(tp==1){//就是特判一下卡卡常而已stk[++tp]=x;return;}int l=lca(stk[tp],x);if(l==stk[tp]){stk[++tp]=x;return;}while(tp>1&&dfn[stk[tp-1]]>=dfn[l]) add1(stk[tp-1],stk[tp]),tp--;if(l!=stk[tp]){add1(l,stk[tp]);stk[tp]=l;}stk[++tp]=x;
}
bool cmp(int x,int y){return dfn[x]<dfn[y];
}
int main(){int x,y,z,s;scanf("%d",&n);for(int i=1;i<n;i++){scanf("%d%d%d",&x,&y,&z);add(x,y,z),add(y,x,z);}dfs1(1,-1);dfs2(1,1);scanf("%d",&q);for(int i=1;i<=q;i++){ stk[tp=1]=1;scanf("%d",&s);for(int j=1;j<=s;j++)scanf("%d",&a[j]);sort(a+1,a+s+1,cmp);for(int j=1;j<=s;j++) ins(a[j]);while(tp) add1(stk[tp-1],stk[tp]),tp--;}
}

---

例题：

P2495 [SDOI2011]消耗战
模板题，建虚树，求一下树根到每个点的经过的边的边权最小值minn，e代表儿子
$dp[x]=min(minn[x],{\sum }_{i=e[x]}minn[i])$

不难，请读者自行思考。
代码：（这里是迭代实现）

#include<bits/stdc++.h>
using namespace std;
int dfn[250010],dep[250010],siz[250010],n,q;
int top[250010],fa[250010],stk[250010],son[250010],tot,tp;
int e[500010],w[500010],nxt[500010],head[250010],cnt;
int a[250010],minn[250010];
long long sum[250010];
void add(int x,int y,int z){cnt++;e[cnt]=y;w[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
}
void dfs1(int x,int f){fa[x]=f;siz[x]=1;dfn[x]=++tot;for(int i=head[x];i;i=nxt[i])if(e[i]!=f){int y=e[i];dep[y]=dep[x]+1;minn[y]=min(minn[x],w[i]);dfs1(y,x);siz[x]+=siz[y];if(siz[y]>siz[son[x]])son[x]=y;}
}
void dfs2(int x,int t){top[x]=t;if(son[x]==0) return;else dfs2(son[x],t);for(int i=head[x];i;i=nxt[i])if(top[e[i]]==0) dfs2(e[i],e[i]);
}
int lca(int x,int y){while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]]) swap(x,y);x=fa[top[x]];}if(dep[x]>dep[y]) swap(x,y);return x;
}
void add1(int x,int y){//cout<<x<<" "<<y<<endl;if(x==y) return;sum[x]+=min(sum[y],minn[y]+0ll);
}
void ins(int x){if(tp==1){sum[x]=minn[x];stk[++tp]=x;return;}int l=lca(stk[tp],x);//cout<<stk[tp]<<" "<<x<<" lca:"<<l<<endl;if(l==stk[tp]) return;while(tp>1&&dfn[stk[tp-1]]>=dfn[l]) add1(stk[tp-1],stk[tp]),tp--;if(l!=stk[tp]){sum[l]=0;add1(l,stk[tp]);stk[tp]=l;}sum[x]=minn[x];stk[++tp]=x;
}
bool cmp(int x,int y){return dfn[x]<dfn[y];
}
int main(){int x,y,z,s;scanf("%d",&n);for(int i=1;i<n;i++){scanf("%d%d%d",&x,&y,&z);add(x,y,z),add(y,x,z);}minn[1]=2e9;dfs1(1,-1);dfs2(1,1);scanf("%d",&q);for(int i=1;i<=q;i++){ sum[1]=0;stk[tp=1]=1;scanf("%d",&s);for(int j=1;j<=s;j++)scanf("%d",&a[j]);sort(a+1,a+s+1,cmp);for(int j=1;j<=s;j++) ins(a[j]);while(tp) add1(stk[tp-1],stk[tp]),tp--;printf("%lld\n",sum[1]);}
}

这篇关于虚树详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---