【七十六】【算法分析与设计】2435. 矩阵中和能被 K 整除的路径,87. 扰乱字符串,三维动态规划

本文主要是介绍【七十六】【算法分析与设计】2435. 矩阵中和能被 K 整除的路径,87. 扰乱字符串,三维动态规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2435. 矩阵中和能被 K 整除的路径

给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往 下 或者往 右 ，你想要到达终点 (m - 1, n - 1) 。

• 请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 10(9)7 取余 的结果。

示例 1：

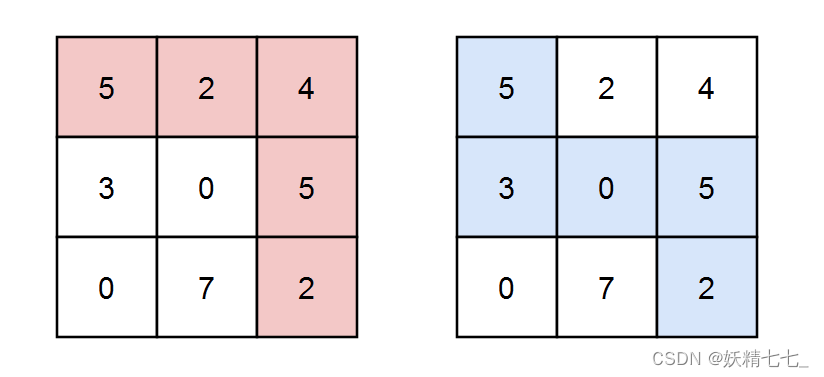
输入：grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 输出：2 解释：有两条路径满足路径上元素的和能被 k 整除。 第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。 第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

示例 2：

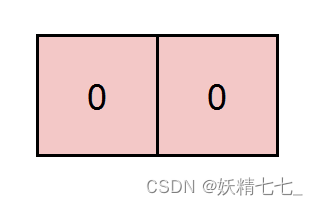
输入：grid = [[0,0]], k = 5 输出：1 解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

示例 3：

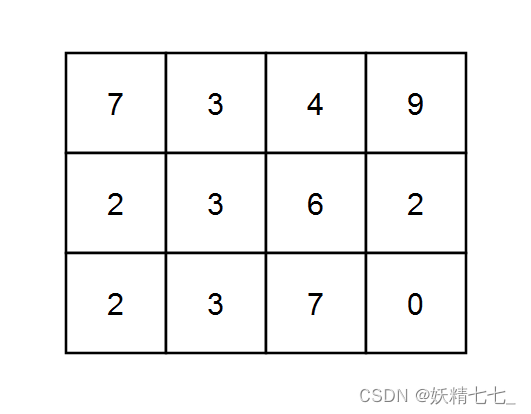
输入：grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 输出：10 解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示：

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 5 * 10(4)

• 1 <= m * n <= 5 * 10(4)

• 0 <= grid[i][j] <= 100

• 1 <= k <= 50

1.

定义f函数,希望将已知信息扔进去加工出我们希望的结果.

我们希望得到从(0,0)位置开始到右下角路径和对k取余为0的路径数.

可以定义f函数从(i,j)位置开始到右下角路径和对k取余为r的路径数.

因此我们需要得到f(0,0,0)的结果.

2.

我们只走一步,从(i,j)位置开始到右下角路径和对k取余为r的路径数.

走一步的结果是(i+1,j)位置或者(i,j+1)位置,能不能找到两者的等价关系.

可以将(i,j)位置的元素值假设为a,走一步位置到右下角的路径和假设为b.

(a+b)%k=r,等价于(a%k+b%k)%k=r.

a%k范围是[0,k-1],b%k范围是[0,k-1].

a%k+b%k范围是[0,2*k-1].

r的范围是[0,k-1].

因此a%k+b%k=r或者r+k.

b%k=r-a%k或者r+k-a%k

b%k=(r+k-a%k)%k.

因此从(i,j)位置开始到右下角路径和对k取余为r的路径数.等价于走一步开始到右下角路径和对k取余为(r+k-a%k)%k的路径数.

3.

处理边界情况,先把状态转移方程写出来,dp[i][j][r]=dp[i+1][j][(r+k-a%k)%k]+dp[i][j+1][(r+k-a%k)%k].

越界的情况是i或者j.很容易知道越界返回0即可.

思考basecase情况,也就是最基本的可以直接得出答案的情况.

也就是当前位置是右下角位置,此时对k取余为r的路径数只需要判断当前元素对k取余是不是等于r即可.

#include <vector>
using namespace std;class Solution {
public:vector<vector<int>> grid; // 定义一个二维数组用于存储输入的网格int k, n, m; // k为路径和需要被整除的数，n和m分别为网格的行数和列数vector<vector<vector<int>>> dp; // 定义一个三维动态规划数组，用于存储中间结果const int MOD = 1e9 + 7; // 定义一个大数作为模数，以防止结果过大// 初始化动态规划数组的辅助函数void solveInit() {n = grid.size(), m = grid[0].size(); // 更新网格的行数和列数dp.clear(); // 清空之前的动态规划数组// 重新初始化动态规划数组的大小为n*m*kdp.resize(n, vector<vector<int>>(m, vector<int>(k, -1)));}// 深度优先搜索的递归函数，用于计算满足条件的路径数目int dfs(int i, int j, int r) {// 如果当前位置超出网格范围，则无法继续移动，返回0if (i >= n || j >= m)return 0;// 如果到达终点，检查路径和是否能被k整除if (i == n - 1 && j == m - 1)return (grid[i][j] % k == r) ? 1 : 0;// 如果当前状态已经在dp数组中计算过，则直接返回结果if (dp[i][j][r] != -1)return dp[i][j][r];int newR = (r + k - (grid[i][j] % k)) % k; // 计算新的路径和对应的余数// 递归计算向下移动和向右移动到达终点的路径数目，并取模dp[i][j][r] = (dfs(i + 1, j, newR) + dfs(i, j + 1, newR)) % MOD;return dp[i][j][r];}// 主函数，用于计算满足条件的路径数目int numberOfPaths(vector<vector<int>>& _grid, int _k) {grid = _grid; // 更新输入的网格k = _k; // 更新k的值solveInit(); // 初始化动态规划数组// 从起点(0, 0)开始，路径和的初始余数为0，递归计算路径数目return dfs(0, 0, 0);}
};

87. 扰乱字符串

使用下面描述的算法可以扰乱字符串 s 得到字符串 t ：

1. 如果字符串的长度为 1 ，算法停止

2. 如果字符串的长度 > 1 ，执行下述步骤：

   1. 在一个随机下标处将字符串分割成两个非空的子字符串。即，如果已知字符串 s ，则可以将其分成两个子字符串 x 和 y ，且满足 s = x + y 。

   2. 随机 决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即，在执行这一步骤之后，s 可能是 s = x + y 或者 s = y + x 。

   3. 在 x 和 y 这两个子字符串上继续从步骤 1 开始递归执行此算法。

给你两个 长度相等 的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：s1 = "great", s2 = "rgeat" 输出：true 解释：s1 上可能发生的一种情形是： "great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串 "gr/eat" --> "gr/eat" // 随机决定：「保持这两个子字符串的顺序不变」 "gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割 "g/r / e/at" --> "r/g / e/at" // 随机决定：第一组「交换两个子字符串」，第二组「保持这两个子字符串的顺序不变」 "r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法，将 "at" 分割得到 "a/t" "r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定：「保持这两个子字符串的顺序不变」 算法终止，结果字符串和 s2 相同，都是 "rgeat" 这是一种能够扰乱 s1 得到 s2 的情形，可以认为 s2 是 s1 的扰乱字符串，返回 true

示例 2：

输入：s1 = "abcde", s2 = "caebd" 输出：false

示例 3：

输入：s1 = "a", s2 = "a" 输出：true

提示：

• s1.length == s2.length

• 1 <= s1.length <= 30

• s1 和 s2 由小写英文字母组成

1.

s1[i,j]区间是否可以转化为s2[x,y]区间.f函数定义.

走一步,枚举所有分割的情况,对于每一种情况考虑交换或者不交换.

class Solution {
public:string s1, s2; // 声明两个字符串s1和s2int n; // 字符串的长度vector<vector<vector<vector<int>>>> dp; // 声明一个四维动态规划数组dp// 初始化动态规划数组的辅助函数void solveinit() {n = s1.size(); // 获取字符串s1的长度dp.clear(), // 清空之前的动态规划数组dp.resize(n, vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(n, -1)))); // 初始化dp数组}// 深度优先搜索的递归函数，用于判断s2是否是s1的扰乱字符串bool dfs(int i, int j, int x, int y) {// 如果当前状态已经在dp数组中计算过，则直接返回结果if (dp[i][j][x][y] != -1)return dp[i][j][x][y];// 如果子串长度为1，判断对应字符是否相等if (i == j) {dp[i][j][x][y] = s1[i] == s2[x];return s1[i] == s2[x];}bool flag = false; // 初始化标志位为false// 枚举s1的子串分割点for (int k = 0; k < j - i; k++) {// 情况1：保持s1的子串顺序，判断s2的对应子串是否满足条件flag |= (dfs(i, i + k, x, x + k) && dfs(i + k + 1, j, x + k + 1, y));// 情况2：交换s1的子串顺序，判断s2的对应子串是否满足条件flag |= (dfs(i, i + k, y - k, y) && dfs(i + k + 1, j, x, y - k - 1));}// 存储当前状态的计算结果dp[i][j][x][y] = flag;return flag; // 返回当前状态的计算结果}// 主函数，用于判断s2是否是s1的扰乱字符串bool isScramble(string _s1, string _s2) {s1 = _s1, s2 = _s2; // 更新输入的两个字符串solveinit(); // 初始化动态规划数组// 从整个字符串的起始位置开始判断return dfs(0, n - 1, 0, n - 1);}
};

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！

这篇关于【七十六】【算法分析与设计】2435. 矩阵中和能被 K 整除的路径,87. 扰乱字符串,三维动态规划的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---