本文主要是介绍高级数据结构与算法期中测试题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、判断题
1、In dynamic programming algorithms, some results of subproblems have to be stored even they do not compose the optimal solution of a larger problem.
T F
解析:T。在动态规划算法中,必须存储子问题的某些结果,因为他们可能需要用来做进一步的比较来产生更大问题的最优解,无论它们最终能不能构成更大问题的最优解,都需要把结果存储。
2、After inserting { 1, 2, 3, 4, 5, 6, 7 } into an initially empty red-black tree, then the number of black nodes in the red-black tree is 4.
T F
解析:T。如果要把1, 2, 3, 4, 5, 6, 7按顺序插入一棵空的红黑树,顺序如下:

因此其中黑色节点确实是4个,正确。
3、If the depth of an AVL tree with nodes { 1, 2, 3, 4 } is 3 (the depth of the root is 1), then it is possible for node 4 to be the root.
T F
解析:F。如果节点为 { 1, 2, 3, 4 } 的 AVL 树的深度为 3(根的深度为 1),则其可能为:
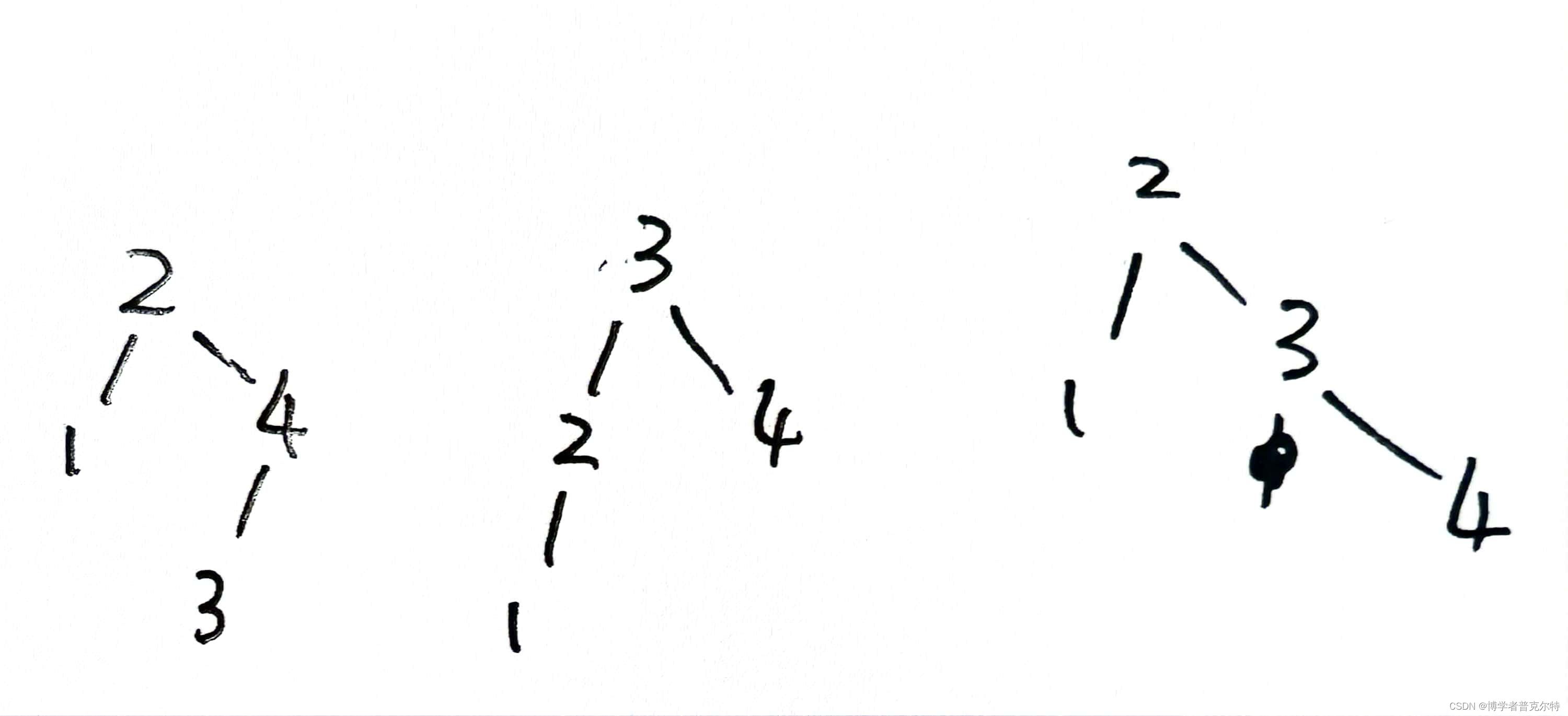
因此,不可能4为根(其实1和4都不行,因为如果这样最大或最小值作为根树两侧必然不平衡)。
4、Inserting a node into a binomial heap with 7 nodes costs less time than inserting a number into a binomial heap with 11 nodes.
T F
解析:F。我们可以看到,如果要把一个元素插入元素为7和11的二项队列,其过程为: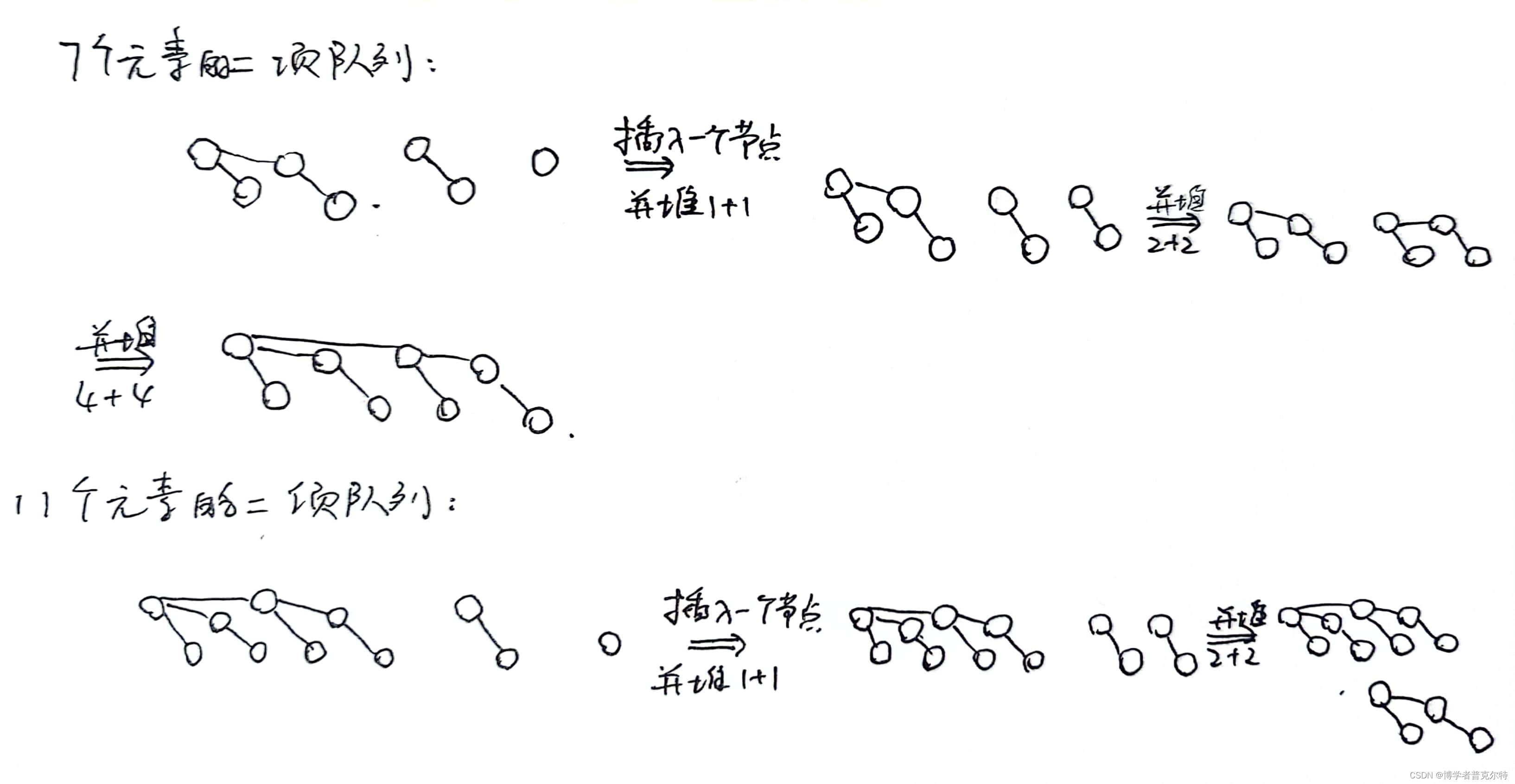
我们可以发现插入元素为7的二项队列多一次并堆操作,故时间更长,错误。
5、For a B+ tree with order M and N keys, the time complexity of find operations is
T F
解析:T。N个元素的B+树的树高大约为,而因为查找过程中只需要按照范围逐层下降查找,因此时间复杂度为
。
6、While accessing a term by hashing in an inverted file index, range searches are inexpensive.
T F
解析:F。在倒排文件索引中进行范围搜索可能会比精确匹配搜索更昂贵,因为它们需要遍历倒排索引的大部分来识别所有符合指定范围的文档。
7、In a Turnpike Reconstruction Problem, given distance set D = { 1,2,3,4,5,6 } , is the only solution provided that x1=0.
T F
解析:F。其实这个题很显然,但是当时做的时候应该是没有仔细想清楚。对于距离集合为 { 1,2,3,4,5,6 } ,我们有(N-1)*N/2=6,得到N=4(至于为什么这样算,是因为距离为两点之间产生,因此n个点产生个距离,也就是(n-1)*n/2)。因此一共4个点,那么其实很显然1,3,2这样三段距离可以构成满足条件,此时的解为{0,1,4,6}。但是如果我们做一个中心对称,很显然2,3,1这样三段距离也可以构成满足条件,此时的解为{0,2,5,6},故不是唯一解,错误。
8、In the leftist heap, the null path length of the right path will be less than or equal to the null path length of any other path originating from the root.
T F
解析:T。在左倾堆中,每一个节点的右侧npl长度要小于或等于左侧的npl。而由于源于根的任意一条左路径的npl都需要长于右侧npl长度,因此右路径的npl长度小于或等于源自根的任何其他路径的npl长度,正确。
9、By the master theorem, the solution to the recurrence is
T F
解析:F。由于主定理:
这篇关于高级数据结构与算法期中测试题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




