数学之美系列二十四 -- 谈谈动态规划与如何设计动态规划算法

本文主要是介绍数学之美系列二十四 -- 谈谈动态规划与如何设计动态规划算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数学之美——动态规划

今年九月二十三日，Google、T-Mobile 和 HTC 宣布了第一款基于开源操作系统 Android 的 3G 手机，其中一个重要的功能是利用全球卫星定位系统实现全球导航。这个功能在其它手机中早已使用，并且早在五六年前就已经有实现这一功能的车载设备出售。其中的关键技术只有两个：第一是利用卫星定位；第二根据用户输入的起终点，在地图上规划最短路线或者最快路线。后者的关键算法是计算机科学图论中的动态规划（Dynamic Programming）的算法。

在图论（请见拙著《图论和网络爬虫》）中，一个抽象的图包括一些节点和连接他们的弧。比如说中国公路网就是一个很好的"图"的例子：每个城市一是个节点，每一条公路是一个弧。图的弧可以有权重，权重对应于地图上的距离或者是行车时间、过路费金额等等。图论中很常见的一个问题是要找一个图中给定两个点之间的最短路径（shortest path）。比如，我们想找到从北京到广州的最短行车路线或者最快行车路线。当然，最直接的笨办法是把所有可能的路线看一遍，然后找到最优的。这种办法只有在节点数是个位数的图中还行得通，当图的节点数（城市数目）有几十个的时候，计算的复杂度就已经让人甚至计算机难以接受了，因为所有可能路径的个数随着节点数的增长而成呈指数增长（或者说几何级数），也就是说每增加一个城市，复杂度要大一倍。显然我们的导航系统中不会用这种笨办法。

所有的导航系统采用的都是动态规划的办法（Dynamic Programming），这里面的规划（programming）一词在数学上的含义是"优化"的意思，不是计算机里面编程的意思。它的原理其实很简单。以上面的问题为例，当我们要找从北京到广州的最短路线时，我们先不妨倒过来想这个问题：假如我们找到了所要的最短路线（称为路线一），如果它经过郑州，那么从北京到郑州的这条子路线（比如是北京-> 保定->石家庄->郑州，称为子路线一），必然也是所有从北京到郑州的路线中最短的。否则的话，我们可以假定还存在从北京到郑州更短的路线（比如北京->济南->徐州->郑州，称为子路线二），那么只要用这第二条子路线代替第一条，我们就可以找到一条从北京到广州的全程更短的路线（称为路线二），这就和我们讲的路线一是北京到广州最短的路线相矛盾。其矛盾的根源在于，我们假设的子路线二或者不存在，或者比子路线一还来得长。

在实际实现算法时，我们又正过来解决这个问题，也就是说，要想找到从北京到广州的最短路线，先要找到从北京到郑州的最短路线。当然，聪明的读者可能已经发现其中的一个"漏洞"，就是我们在还没有找到全程最短路线前，不能肯定它一定经过郑州。不过没有关系，只要我们在图上横切一刀，这一刀要保证将任何从北京到广州的路一截二，如下图。

那么从广州到北京的最短路径必须经过这一条线上的某个城市（图中蓝色的菱形）。我们可以先找到从北京出发到这条线上所有城市的最短路径，最后得到的全程最短路线一定包括这些局部最短路线中的一条，这样，我们就可以将一个"寻找全程最短路线"的问题，分解成一个个小的寻找局部最短路线的问题。只要我们将这条横切线从北京向广州推移，直到广州为止，我们的全程最短路线就找到了。这便是动态规划的原理。采用动态规划可以大大降低最短路径的计算复杂度。在我们上面的例子中，每加入一条横截线，线上平均有十个城市，从广州到北京最多经过十五个城市，那么采用动态规划的计算量是 10×10×15，而采用穷举路径的笨办法是 10 的 15 次方，前后差了万亿倍。

那么动态规划和我们的拼音输入法又有什么关系呢？其实我们可以将汉语输入看成一个通信问题，而输入法则是一个将拼音串到汉字串的转换器。每一个拼音可以对应多个汉字，一个拼音串就可以对应图论中的一张图，如下：

其中，Y1,Y2,Y3,……,YN 是使用者输入的拼音串，W11,W12,W13 是第一个音 Y1 的候选汉字，W21,W22,W23,W24 是对应于 Y2 的候选汉字，以此类推。从第一个字到最后一个字可以组成很多很多句子，我们的拼音输入法就是要根据上下文找到一个最优的句子。如果我们再将上下文的相关性量化，作为从前一个汉字到后一个汉字的距离，那么，寻找给定拼音条件下最合理句子的问题就变成了一个典型的"最短路径"问题，我们的算法就是动态规划。

上面这两个例子导航系统和拼音输入法看似没什么关系，但是其背后的数学模型却是完全一样的。数学的妙处在于它的每一个工具都具有相当的普遍性，在不同的应用中都可以发挥很大的作用。

如何设计和实现动态规划算法

进行算法设计的时候，时常有这样的体会：如果已经知道一道题目可以用动态规划求解，那么很容易找到相应的动态规划算法并实现；动态规划算法的难度不在于实现，而在于分析和设计—— 首先你得知道这道题目需要用动态规划来求解。本文，我们主要在分析动态规划在算法分析设计和实现中的应用，讲解动态规划的原理、设计和实现。在很多情况下，可能我们能直观地想到动态规划的算法；但是有些情况下动态规划算法却比较隐蔽，难以发现。本文，主要为你解答这个最大的疑惑：什么类型的问题可以使用动态规划算法？应该如何设计动态规划算法？

动态规划第一讲——缓存与动态规划

一、缓存与动态规划

例一：有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第10级台阶有几种不同的走法?

分析：很显然，这道题的对应的数学表达式是F(n)=F(n-1) + F(n-2);其中F(1)=1, F(2)=2。很自然的状况是，采用递归函数来求解：

int  solution(int n){  if(n>0 && n<2) return n;  return solution(n-1) + solution(n-2);  
}

如果我们计算F(10), 先需要计算F(9) F(8); 但是我们计算F(9)的时候，又需要计算F(8)，很明显，F(8)被计算了多次，存在重复计算；同理F(3)被重复计算的次数就更多了。算法分析与设计的核心在于根据题目特点，减少重复计算。在不改变算法结构的情况下，我们可以做如下改进：

int dp[11];  
int  solution(int n){  if(n>0 && n<2) return n;  if(dp[n]!=0) return dp[n];  dp[n] = solution(n-1) + solution(n-2);  return  dp[n];  
}

这是一种递归形似的写法，进一步，我们可以将递归去掉：

int  solution(int n){  int dp[n+1];  dp[1]=1;dp[2]=2;  for (i = 3; i <= n; ++i){  dp[n] = dp[n-1] + dp[n-2];  }  return  dp[n];  
}

当然，我们还可以进一步精简，仅仅用两个变量来保存前两次的计算结果; 这个算法留待读者自己去实现

例二：01背包问题

有n个重量和价值分别为vector<int> weight, vector<int> value的物品；背包最大负重为W，求能用背包装下的物品的最大价值？

输入：n =4
weight=2, 1, 3, 2
value =3, 2, 4, 2
W=5
输出=7

思考一：我们可以采用穷举法，列出n个物品的所有组合形式，从中选取符合条件的最大价值：

采用穷举法，必然需要能够举出所有状态，不重不漏；而如何穷举，方法多种多样,我们的任务是要穷举有n个元素组成的所有子集。而穷举的方法主要有两种—— 递增式（举出1～100之内的所有数字，从1到100）；和分治式的穷举（例如举出n个元素的集合，包含两种—— 含有元素a和不含元素a的）。于是，我们基于穷举法得到背包问题的第一种算法—— 递归与分治。

int rec(int i, int j){//从i到n号物品，选择重量不大于j的物品的最大价值  int res;  if(i==n){  res=0;  }   else if(j< w[i]){  res = rec(i+1, j);  }  else{  res = max(rec(i+1, j), rec(i+1, j-w[i])+v[i]);  }  return res;  
}

调用res(0, W), 即可得到结果. 时间复杂度O(2^n)；我们来分析一下递归调用的情况。

为了偷懒，最后一行没有画出来，但是注意红色的部分，我们会发现(3, 2)这个子问题被计算了两次，很显然，如果问题规模足够大，数据足够多样，这种重复计算导致的时间耗费将更多。

改进：采用递归加缓存的策略
此时，时间复杂度是O(nW); 代码就省略不写了。

思考二：上文中的记忆化搜索，如果可以将递归变为循环，这就是动态规划，对应的数学表达式如下：

dp[i][j] = max(dp[i+1][j], dp[i+1][j-w[i]] + v[i]);//对应的计算表格如下和程序如下：  
void solution(){  fill(dp[n], dp[n]+W, 0);  for (int i = n-1; i >= 0; --i){  for (j = 0; j <= W; ++j){  if(j < w[i]) dp[i][j] = dp[i+1][j];  else dp[i][j] = max(dp[i+1][j], dp[i+!][j-w[i]]+v[i]);  }  }  return dp[0][W];  
}

思考三：递归形式的多样化

我们刚才的递归计算，在i这个维度是逆向的，同样我们可以采用正向的DP。规定dp[i][j]表示前i号物品中能选出重量在j之内的最大价值，则有递推式
dp[i][j] = max(dp[i-1][j] , dp[i-1][j-w[i]] + v[i]);

思考四：我们是如何想到递归算法的？

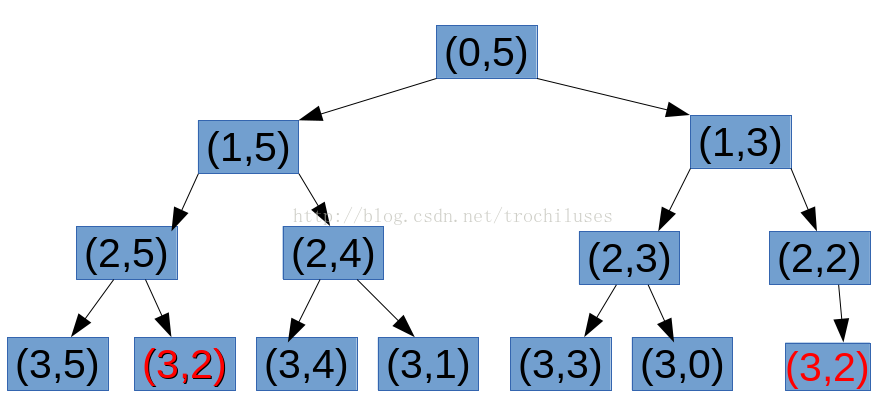
也许，DP算法的难度不在于告诉你这个题目需要用DP求解，然后让你来实现算法。而在于你首先得意识到这道题目需要用递归求解,这里我们通过分析上面的思考步骤来总结DP算法的典型特征：
1>DP算法起源于DC—— 一个问题的解，可以先分解为求解一系列子问题的解，同时包含重叠子问题：于是，我们得到DP算法的第一个黄金准则：某个问题具有独立而重叠的字问题；子问题不独立，没法进行分治；子问题不重叠，没有进行DP的必要，直接用普通的分治法就可以了。
2>DP算法黄金准则2：最优子问题—— 子问题的最优解可以推出原问题的最优解。

我们还是来看上面的那个决策树，很明显，DP的本质就在于缓存。我们寻找DP结果的时候，往往是需要遍历这个树，从中找出最优解。但是有些情况下，我们需要寻找的不是最优解，而是可行解，这个时候往往使用DFS或者循环更为有效，后面，我们会给出例子。此时，我们仅仅需要记得，动态规划的第二个条件—— 最优子问题。

所以算法的设计思路不在于一下子就想到了某个问题可以使用DP算法，而在于先看能不能用穷举法，如果可以用问题可以分解，分治法+穷举可以解决；如果问题包含重叠字问题，并且是求解最优解，那么此时用动态规划。