SPSS之回归分析

本文主要是介绍SPSS之回归分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

SPSS中回归分析功能在【分析】--【回归】--【线性】中进行线性回归分析。对于一元线性回归，可通过【图形】--【旧对话框】--【散点图】绘制因变量y和自变量x的散点图。

通过样本数据建立回归方程后不能立即用于对实际问题的分析和预测，需进行各种统计经验，主要包括：

1. （1）回归方程的拟合优度检验（r检验）；
2. （2）回归方程的显著性检验（F检验）；
3. （3）回归系数的显著性检验（t检验）；

（4）残差分析，即分析残差是否满足“正态、独立、等方差（无异常值）”的前提。在SPSS中，在【分析】--【回归】--【线性】--【绘图】框中，可通过绘制残差的散点图、频率直方图以及正态概率图（P-P图）来完成残差分析。

多元回归分析中变量的筛选问题。一般有向前筛选、向后筛选、逐步筛选三种基本策略。逐步筛选是目前使用较多的一种方法。变量的筛选在【分析】--【回归】--【线性】--【方法】框中选择一种策略来完成回归分析。

残差的独立性检验：DW检验（Durbin-Watson）：

1. DW=4：序列完全负自相关
2. 2<DW<4：序列存在负自相关
3. DW=2：序列无自相关
4. 0<DW<2：序列存在正自相关
5. DW=0：序列完全正自相关

变量的多重共线性测度。一般有以下方式：

1. （1）容忍度。取值∈(0,1)，越接近0表示多重共线性越强；越接近1表示多重共线性越弱。
2. （2）方差膨胀因子（VIF）。VIF≥1。多重共线性越弱，VIF越接近1；多重共线性越强，VIF越大。通常，如果VIF≥10，说明解释变量间有严重的多重共线性。
3. （3）特征根和方差比。如果特征根中，最大特征根的值远远大于其他特征根的值(0.7以上)，说明变量间有很强的多重共线性。如果某个特征根可以同时刻画多个解释变量方差的较大部分比例，说明这些解释变量间有较强的多重共线性。
4. （4）条件指数。条件指数∈[0,10)，多重共线性较弱；条件指数∈[10,100)，多重共线性较强；条件指数≥100时，存在严重多重共线性。

接下来我们运用SPSS来进行实战回归分析！

利用文件高校科研研究.sav,因变量为“论文数”，分析其它变量与因变量的相关性，选择一个变量作为自变量，建立一元回归模型并完成回归的显著性检验。

首先浏览高校科研研究.sav数据文件的基本信息：

变量视图可以看到该数据集有8个字段，字段名分别为：x1,x2,x3,x4,x5,x6,x7,x8。对每个字段的标签分别为‘省市名称’、‘投入人年数’、‘投入高级职称的人数’、‘投入科研事业费（百元）’、‘课题总数’、‘专著数’、‘论文数’、‘获奖数’。

再来看看数据集的具体内容：该数据集共有31个样本数据。

下面我们开始步入回归分析：

第一步我们进行相关性检验：[Analyze]→[Correlate]→[Bivariate Correlations]进行双变量相关性检验。将所有变量都添加到‘Variables’中。

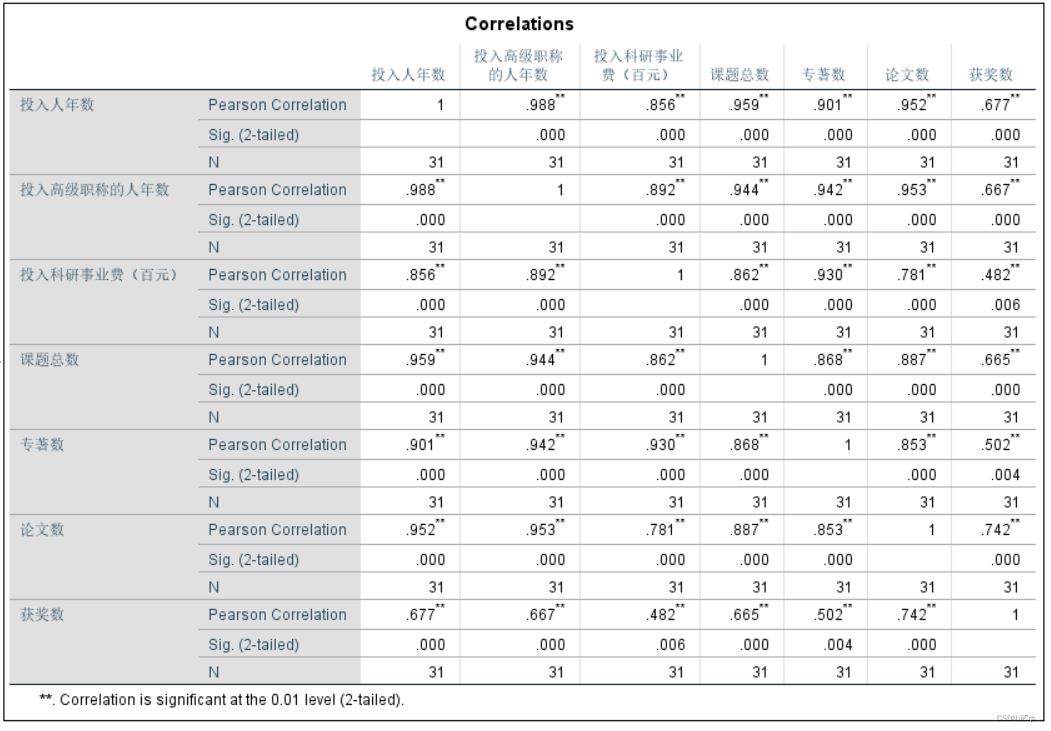因为投入高级职称的人年数与论文数的Pearson相关系数最大，故二者之间的相关性较强，所以选择投入高级职称的人年数作为自变量，论文数为因变量。

一元线性回归建模及回归的显著性检验：

先看看投入高级职称的人年数和论文数的散点图：

选择工具栏[Analyze]→[Regression]→[Linear Regression]。将‘论文数’添加到Dependent中，‘投入高级职称的人数’添加到Independent中。确定输出结果：

由模型汇总表可以看到r检验：样本相关系数r=0.953，样本决定系数r²=0.909，所以回归的拟合优度较好。

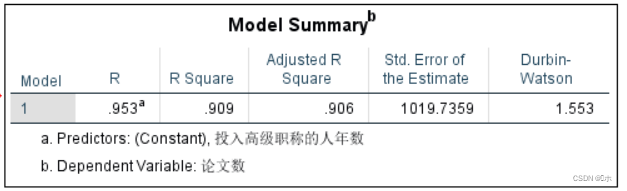
在Anova表可以看F检验：F值=289.715， p值=0.000，p值 ＜α=0.05，所以可以建立回归方程。

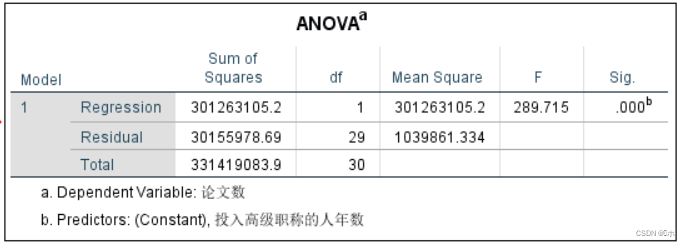
在回归系数表中可以看t检验：回归系数p值=0.000，p值 ＜α=0.05，线性回归显著。

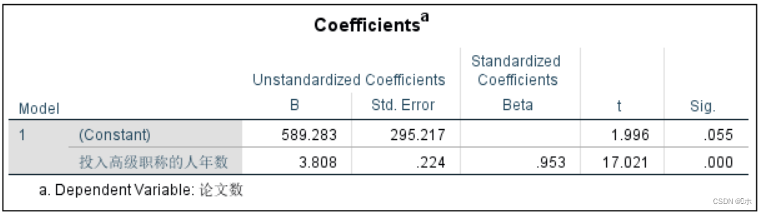
综上三表结果可以确定投入高级职称的人年数作为自变量，论文数为因变量的回归方程为：

残差分析:

标准化残差的频率直方图:

标准化残差的P-P图：

由图可知，标准化残差大部分围绕在对角线附近，所以 标准化残差近似服从正态分布。

标准化残差的散点图：

1. 由图可知， ①标准化残差落入（-3 — 3）内，无异常值。故满足正态分布前提。
2. ②标准化残差随着因变量的增大表现出明显趋势。故满足独立前提。

---

利用文件高校科研研究.sav,应用多元线性回归来分析投入人年数、投入高级职称的人年数、投入科研事业费、专著数、论文数、获奖数对立项课题数的预测效果。请首先采用“输入”策略强制所有自变量进入回归，如需重新建模，再采用逐步法进行回归分析。

（1）“输入法”建模：

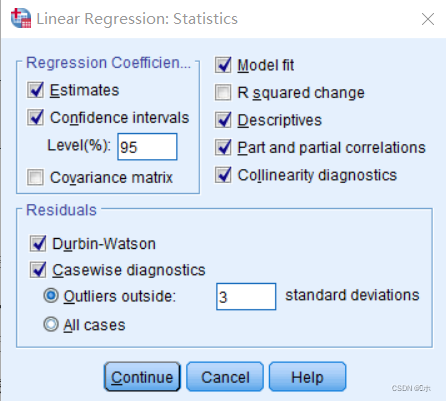
[Analyze]→[Regression]→[Linear Regression]。将‘课题总数’添加到Dependent中，‘投入人年数’、‘投入高级职称的人数’、‘投入科研事业费（百元）’、‘专著数’、‘论文数’、‘获奖数’添加到Independent中。并在’Mode‘中选择‘Enter’方法。在【Statistics】对话框中勾选：

下面查看输出结果：

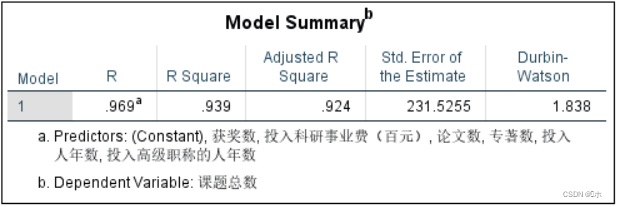
输入/除去的变量表。说明最终进入模型中的变量是哪些：获奖数、投入科研事业费、论文数、专著数、投入人年数、投入高级职称的人年数。

模型摘要表中看r检验：样本相关系数r=0.969，样本决定系数r²=0.939，样本校正决定系数调整后r²=0.924，DW值= 1.838，所以存在正自相关性。 即回归的拟合优度较好。

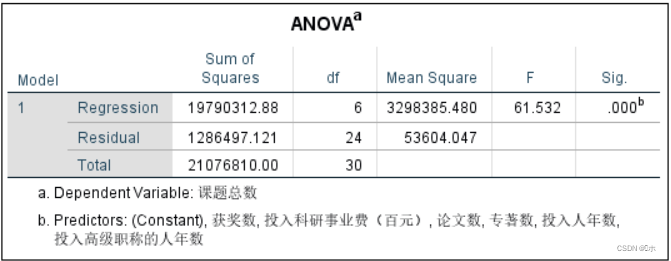
ANOVA表中看F检验：F值=61.532， p值=0.000，p值 ＜ α=0.05，拒绝零假设，认为各复回归系数不全为0，因此，可以建立回归方程。

系数表中看t检验：从回归系数p值，容忍度，方差膨胀因子VIF这三个方面来进行分析。

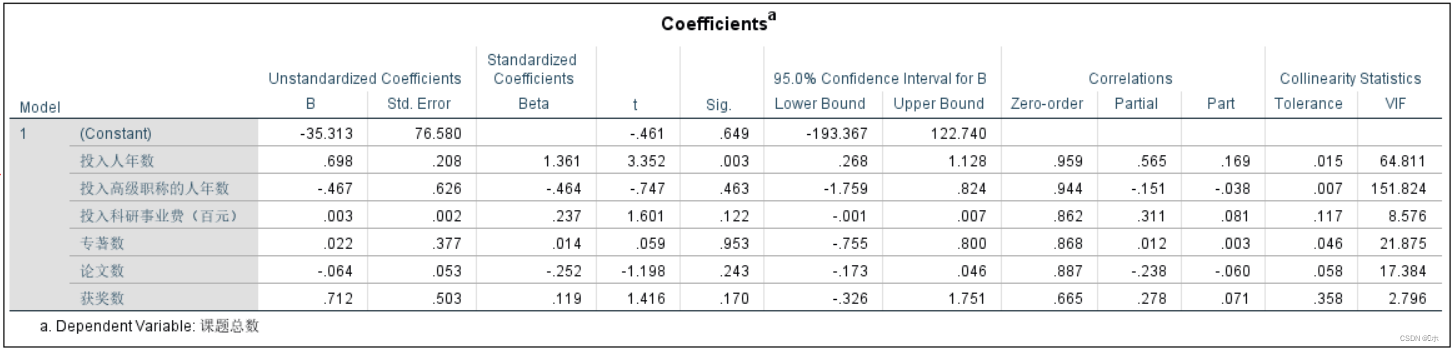结论：  投入人年数、投入高级职称的人年数、专著数、论文数这四个指标的容忍度均＜0.1，方差膨胀因子VIF均＞10。说明解释变量间有严重的多重共线性。其中投入人年数的P值为0.003＜0.05，说明投入人年数对课题总数的影响比较显著。

多重共线性诊断：

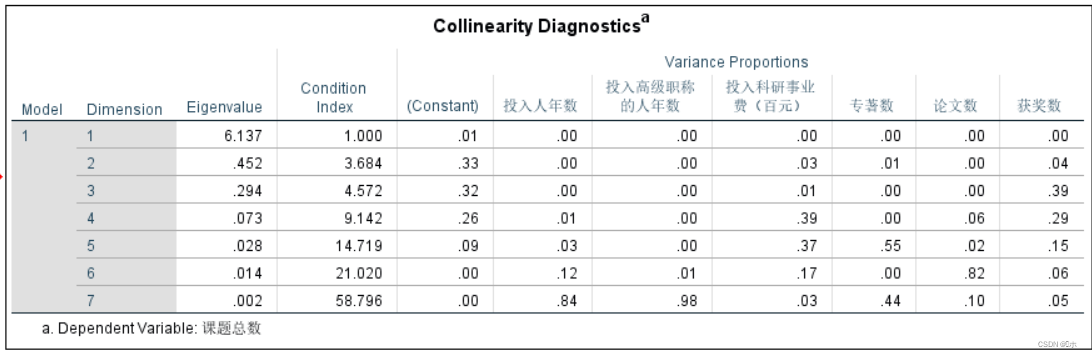
结论：在特征根中，最大特征根的值远远大于其他特征根的值（0.7以上），说明变量间有很强的多重共线性。其中，维度为7的的特征根可以同时刻画投入人年数、投入高级职称的人年数、投入科研事业费、专著数、论文数、获奖数，六个解释变量的方差的较大部分比例，说明这些解释变量间有较强的多重共线性。

从条件指数来看，维度为5、6、7三个的条件指数均在10—100之间，说明他们都有较强的多重共线性。但其中维度为7的的条件指数最大，为58.796，其多重共线性是最强的。

（2）逐步法建模：

在[Linear Regression]对话框中，将’Model‘的方法改为‘Stepwise’即可。

输入/除去的变量表。说明最终进入模型中的变量是投入人年数。

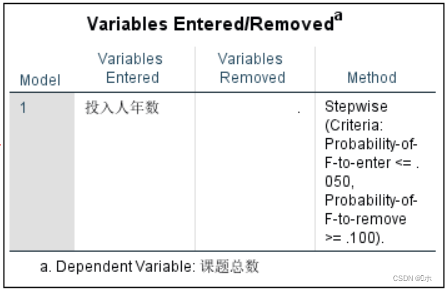
r检验：样本相关系数r=0.959，样本决定系数r²=0.919，调整后r²=0.917，DW值=1.747，所以存在正自相关性。因此回归的拟合优度较好。

F检验：F值=331.018， p值=0.000，p值＜α=0.05，拒绝零假设，认为各复回归系数不全为0，可以建立回归方程。

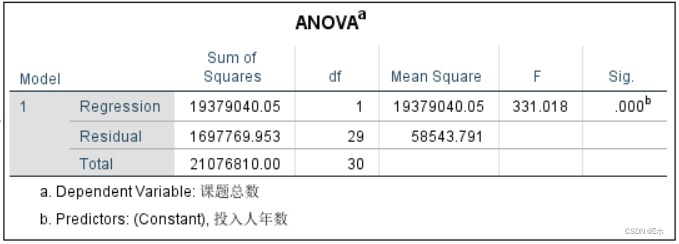
t检验：回归系数p值＜α=0.05，线性回归显著。

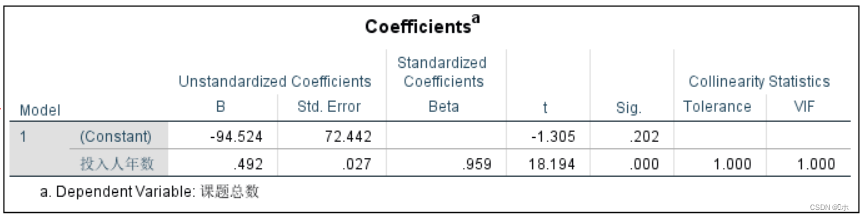
综上：回归方程为：

（3）残差分析：

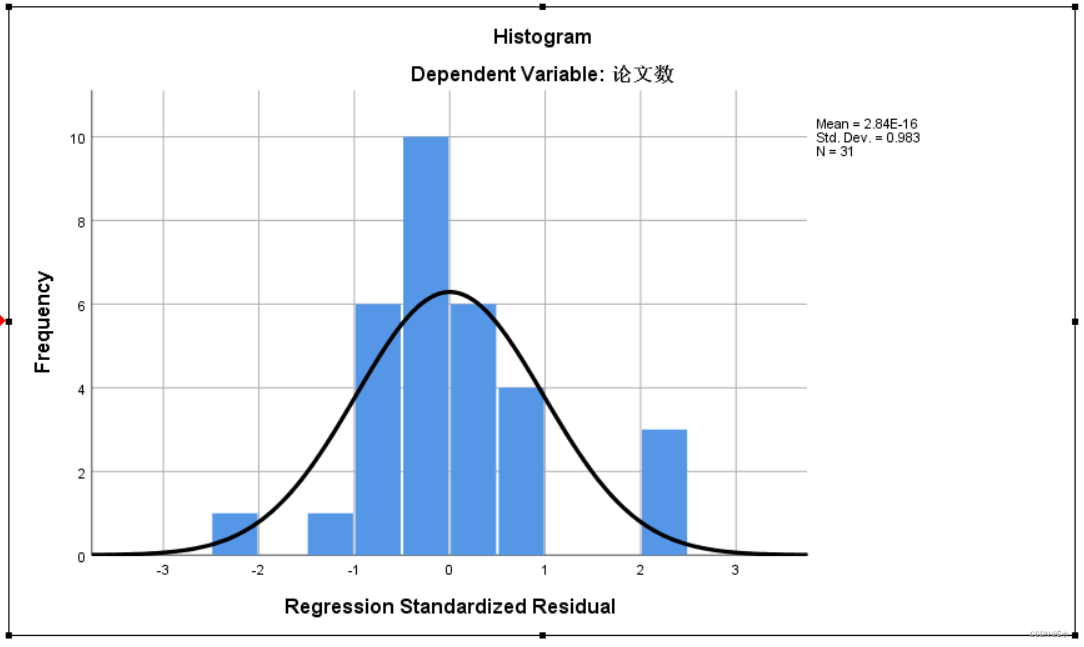
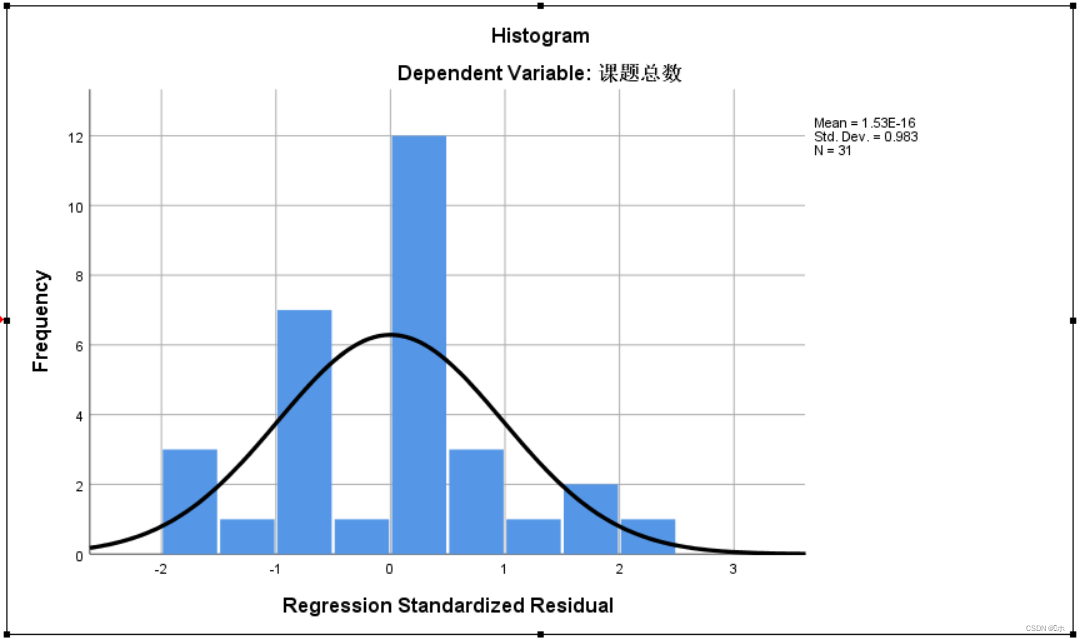
标准化残差的频率直方图：由图可知，标准化残差近似服从正态分布。

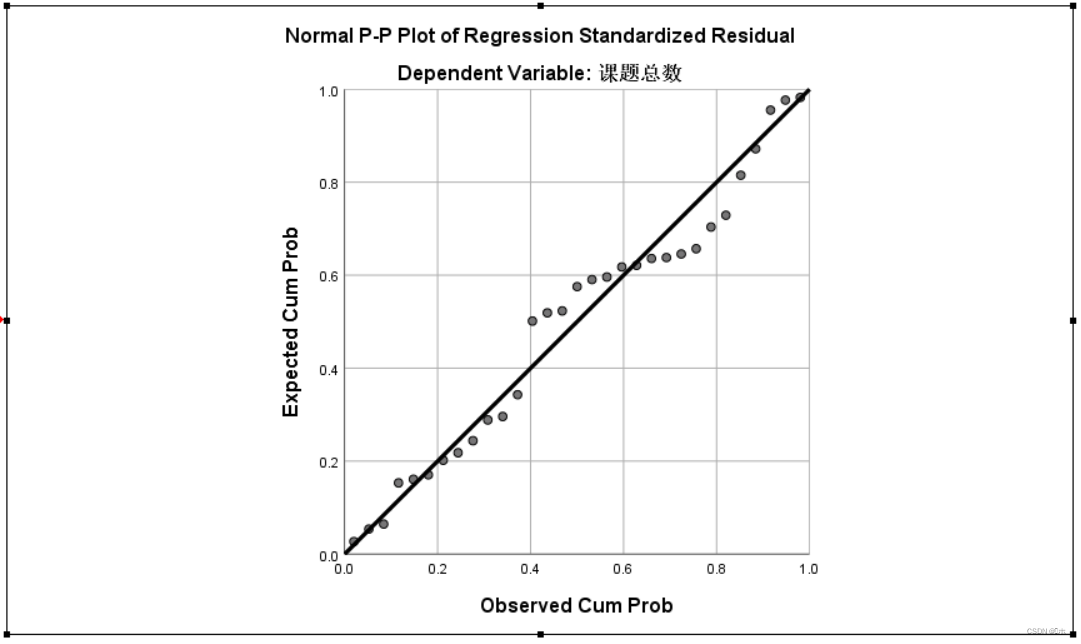
 标准化残差的P-P图：由图可知，标准化残差大部分围绕在对角线附近，所以标准化残差近似服从正态分布。

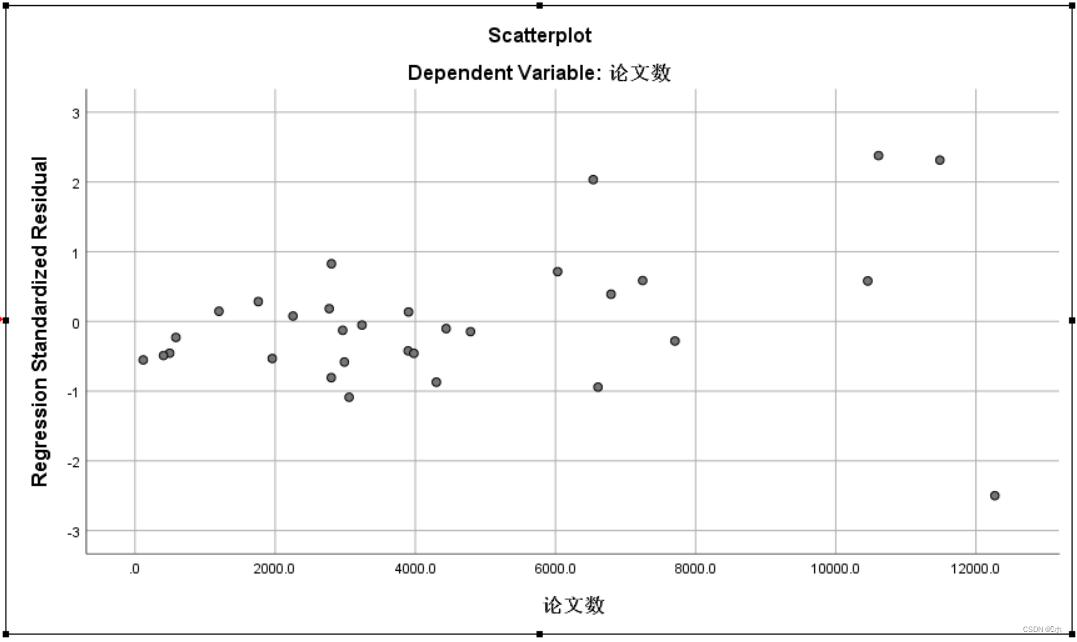
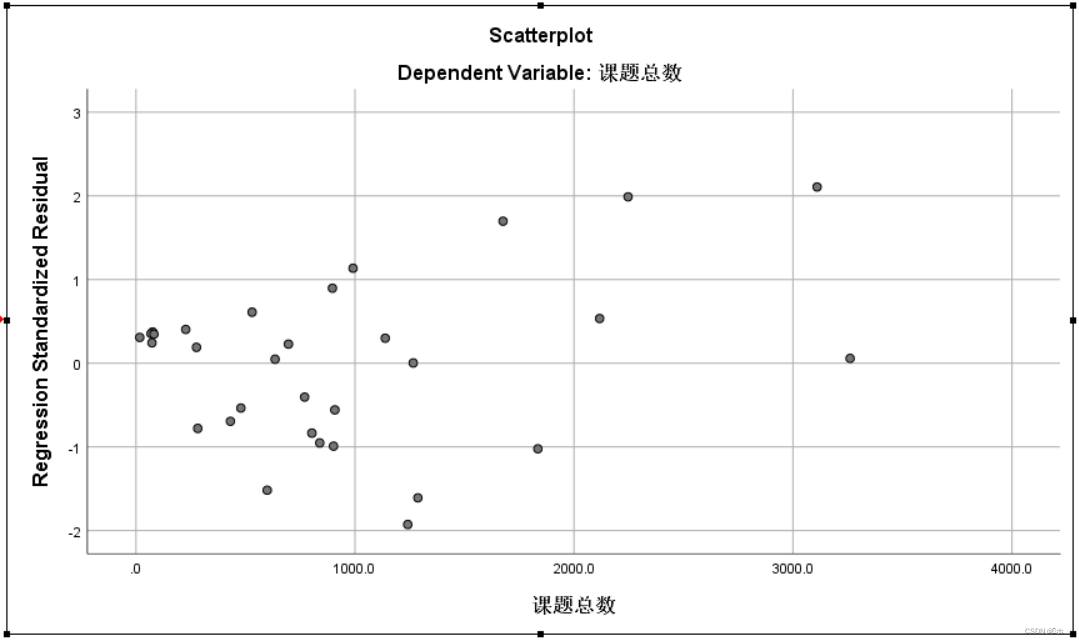
标准化残差的散点图：由图可知，标准化残差落入（-2 — 3）内，有异常值。故满足正态分布前提。标准化残差有随着因变量的增大表现出明显趋势。故满足独立前提。

需要练习原数据的同学，点赞+关注后台私信获取！！!

需要练习原数据的同学，点赞+关注后台私信获取！！!

需要练习原数据的同学，点赞+关注后台私信获取！！!

这篇关于SPSS之回归分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---