本文主要是介绍LeetCode-Q105-从前序与中序遍历序列构造二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【labuladong P26】
【题目地址】https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
【解题思路】https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
【题目】根据一棵树的前序遍历与中序遍历构造二叉树
【思路】前序遍历所得到的节点就是根节点,再更具中序遍历中根节点的位置将中序遍历左右分为左右子树,然后依次自身调用,最后实现二叉树的构建。
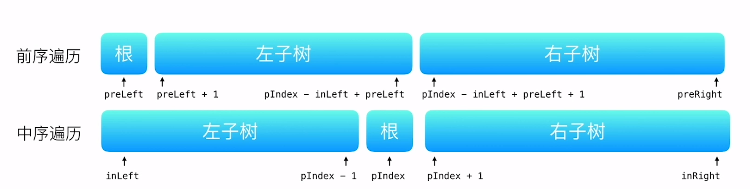
代码如下:
import java.util.HashMap;
import java.util.Map;class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(int x){val = x;}
}
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder){int preLen = preorder.length;int inLen = inorder.length;//合法性判断if(preLen != inLen){throw new RuntimeException("Incorrect input data.");}//构建hashmap存储Map<Integer, Integer> map = new HashMap<>(preLen);for(int i = 0; i < preLen; i++){map.put(inorder[i],i);}return buildTree(preorder, 0, preLen -1, map, 0, inLen -1);}/**@param preorder 前序遍历序列*@param preLeft 前序遍历序列子区间的左边界,可以取到本@param preRight 前序遍历序列子区间的右边界,可以取到*@param map 在中序遍历序列里,数值与下标的对应关系*@param inLeft 中序遍历序列子区间的左边界,可以取到本@param inRight 前序遍历序列子区间的右边界,可以取到*@return*///修改buildTree的方法定义private TreeNode buildTree(int[] preorder, int preLeft, int preRight, Map<Integer, Integer>map, int inLeft, int inRight){//修改递归终止条件if(preLeft > preRight || inLeft > inRight){return null;}//找到根节点并创建int rootVal = preorder[preLeft];TreeNode root = new TreeNode(rootVal);//找到根节点在中序遍历中的位置int pIndex = map.get(rootVal);root.left = buildTree(preorder, preLeft + 1, pIndex - inLeft + preLeft,map, inLeft,pIndex -1);root.right = buildTree(preorder,pIndex - inLeft + preLeft + 1, preRight,map, pIndex + 1, inRight);//最后返回根节点return root;}
}
这篇关于LeetCode-Q105-从前序与中序遍历序列构造二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







