Python 决策树与贝叶斯相关理论知识和例题

本文主要是介绍Python 决策树与贝叶斯相关理论知识和例题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

信息有顺序排列，意思明确
信息无序，意思多
描述信息的混乱度用信息熵

ID3算法

将无序的数据变得更加有序。
信息熵计算公式

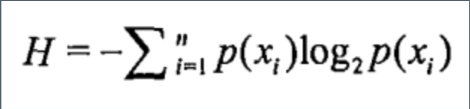
信息增益：

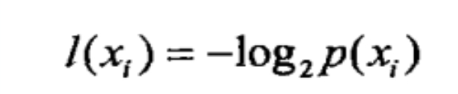
在决策树中，设D为用类别对训练元组的划分，则D的熵表示为：

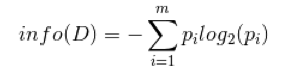
训练元组D按照属性A进行划分，则A对D划分的期望信息为：

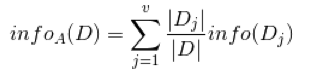
信息增益为两者的差值：

例题

现有如下表格数据，描述根据天气等情况决定是否出去打羽毛球的记录。

Day	Weather	Temperature	Humidity	Wind	Play?
1	Sunny	Hot	Hight	Weak	No
2	Cloudy	Hot	Hight	Weak	Yes
3	Sunny	Mild	Normal	Strong	Yes
4	Cloudy	Mild	Hight	Strong	Yes
5	Rainy	Mild	Hight	Strong	No
6	Rainy	Cool	Normal	Strong	No
7	Rainy	Mild	Hight	Weak	Yes
8	Sunny	Hot	Hight	Strong	No
9	Cloudy	Hot	Normal	Weak	Yes
10	Rainy	Mild	Hight	Strong	No

设We、T、H、Wi、D表示Weather、Temperature、Humidity、Wind、Play?(是否打羽毛球）。下面计算各属性的信息增益:

D：5个Yes 5个No
集合(1,…,10)的信息熵:
$$info(D)=-\frac{1}{2}lo{g}_2\frac{1}{2}-\frac{1}{2}lo{g}_2\frac{1}{2}=1$$
按照属性We进行划分D，则We对D划分的期望：
Sunny 0.3 ------> 1个Yes 2个No
Cloudy 0.3 ------> 3个Yes
Rainy 0.4 --------> 1个Yes 3个No
$$inf{o}_{W}e(D)=0.3\ast (-\frac{1}{3}lo{g}_2\frac{1}{3}-\frac{2}{3}lo{g}_2\frac{2}{3})+0.3\ast (-1\ast lo{g}_{2}1)+0.4\ast (-\frac{1}{4}lo{g}_2\frac{1}{4}-\frac{3}{4}lo{g}_2\frac{3}{4})=0.6$$
利用python计算结果:

We的信息增益：
$$gain(We)=info(D)-inf{o}_{W}e(D)=1-0.6=0.4$$

同上得到T、H、Wi的信息增益:
$$inf{o}_T(D)=0.4\ast (-\frac{2}{4}lo{g}_2\frac{2}{4}-\frac{2}{4}lo{g}_2\frac{2}{4})+0.5\ast (-\frac{3}{5}lo{g}_2\frac{3}{5}-\frac{2}{5}lo{g}_2\frac{2}{5})+0=0.885$$
$$inf{o}_H(D)=0.7\ast (-\frac{3}{7}lo{g}_2\frac{3}{7}-\frac{4}{7}lo{g}_2\frac{4}{7})+0.3\ast (-\frac{2}{3}lo{g}_2\frac{2}{3}-\frac{1}{3}lo{g}_2\frac{1}{3})=0.956$$
$$inf{o}_{W}i(D)=0.4\ast (-\frac{3}{4}lo{g}_2\frac{3}{4}-\frac{1}{4}lo{g}_2\frac{1}{4})+0.6\ast (-\frac{2}{4}lo{g}_2\frac{2}{4}-\frac{2}{4}lo{g}_2\frac{2}{4})=0.925$$
$$gain(T)=info(D)-inf{o}_T(D)=1-0.885=0.115$$
$$gain(H)=info(D)-inf{o}_H(D)=1-0.956=0.044$$
$$gain(Wi)=info(D)-inf{o}_{W}i(D)=1-0.925=0.075$$
综上得到Weather、Temperature、Humidity、Wind的信息增益分别为0.400、0.115、0.044和0.075。
因为Weather具有最大的信息增益，所以第一次分裂选择Weather为分裂属性，第二次分裂选择Temperature为分裂属性，第三次分裂选择Wind为分裂属性，分裂后的结果如下图所示：

贝叶斯

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

例1

现分别有A、B两个容器，在容器A里分别有7个红球和3个白球，在容器B中有1个红球和9个红球。现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器A的概率是多少？
解：假设抽出红球的事件为B，选中容器A为事件A，则有：
$$P(B)=\frac{8}{20},P(A)=\frac{1}{2}$$
$$在容器A中抽出红球的概率：P(B|A)=\frac{7}{10}$$
$$则抽出红球来自A容器的概率：P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{\frac{7}{10}\ast \frac{1}{2}}{\frac{8}{20}}=\frac{7}{8}=0.875$$

例2

一座别墅在过去的20年里一共发生过2次被盗，别墅的主人有一条狗，狗平均每周晚上叫3次，在盗贼侵入时狗叫的概率被估计为0.9，问：在狗叫的时候发生盗贼入侵的概率是多少？
解：假设被盗的事件为A，狗叫的事件为B，则有：
$$P(A)=\frac{2}{20\ast 365},P(B)=\frac{3}{7},P(B|A)=0.9$$
$$则在狗叫的时候盗贼入侵的概率为：P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{0.9\ast \frac{2}{20\ast 365}}{\frac{3}{7}}=0.00058$$

朴素贝叶斯

朴素：独立性假设，假设各个特征之间是独立不相关的。

朴素贝叶斯的好处：在特征较多且数据少的情况下，还能计算出我们想要的结果。

例题

有一个如下表格：

帅？	性格好？	身高？	上进？	嫁与否
帅	不好	矮	不上进	不嫁
不帅	好	矮	上进	不嫁
帅	好	矮	上进	嫁
不帅	好	高	上进	嫁
帅	不好	矮	上进	不嫁
不帅	不好	矮	上进	不嫁
帅	好	高	不上进	嫁
不帅	好	高	上进	嫁
帅	好	高	上进	嫁
不帅	不好	高	上进	嫁
帅	好	矮	不上进	不嫁
帅	好	矮	不上进	不嫁

问题：如果一对男女朋友，男生的四个特点分别是不帅，性格不好，身高矮，不上进，判断女生是嫁还是不嫁？

根据贝叶斯公式有：
$$P(嫁｜不帅、性格不好、身高矮、不上进)$$
$$=\frac{P(不帅、性格不好、身高矮、不上进|嫁)P(嫁)}{P(不帅、性格不好、身高矮、不上进)}$$
$$给得数据无法计算P(不帅、性格不好、身高矮、不上进|嫁)和$$

$$P(不帅、性格不好、身高矮、不上进)$$

这时朴素贝叶斯起到作用，由于朴素贝叶斯的独立性假设，假设各个特征之间是独立不相关的，所以上面的公式就可以转化为：
$$P(嫁｜不帅、性格不好、身高矮、不上进)=\frac{P(不帅、性格不好、身高矮、不上进|嫁)P(嫁)}{P(不帅、性格不好、身高矮、不上进)}$$

$$=\frac{P(不帅｜嫁)\ast P(性格不好|嫁)\ast P(身高矮|嫁)\ast P(不上进|嫁)\ast P(嫁)}{P(不帅)\ast P(性格不好)\ast P(身高矮)\ast P(不上进)}$$

$$=\frac{\frac{3}{6}\ast \frac{1}{6}\ast \frac{1}{6}\ast \frac{1}{6}\ast \frac{6}{12}}{\frac{5}{12}\ast \frac{4}{12}\ast \frac{7}{12}\ast \frac{4}{12}}=0.043$$
同理计算：
$$P(不嫁｜不帅、性格不好、身高矮、不上进)=0.964$$
明显P(不嫁｜不帅、性格不好、身高矮、不上进) > P(嫁｜不帅、性格不好、身高矮、不上进)，可以判断为不嫁。

参考

https://blog.csdn.net/amds123/article/details/70173402

这篇关于Python 决策树与贝叶斯相关理论知识和例题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---