本文主要是介绍python 数学+减治、下一个排列法、DFS回溯法实现:第 k 个排列【LeetCode 题目 60】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。
会一些的技术:数据分析、算法、SQL、大数据相关、python
欢迎加入社区:码上找工作
作者专栏每日更新:
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化:企业实战案例
备注说明:方便大家阅读,统一使用python,带必要注释,公众号 数据分析螺丝钉 一起打怪升级
题目描述
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
- “123”
- “132”
- “213”
- “231”
- “312”
- “321”
给定 n 和 k,返回第 k 个排列。
输入格式
- n:一个整数,表示集合的大小。
- k:一个整数,表示所求的排列序号。
输出格式
- 返回一个字符串,表示第
k个排列。
示例 1
输入: n = 3, k = 3
输出: "213"
示例 2
输入: n = 4, k = 9
输出: "2314"
方法一:数学 + 减治法
解题步骤
- 计算阶乘:首先计算所有小于等于
n的数字的阶乘,这有助于后续确定每位数字的位置。 - 确定每位数字:从最高位开始,根据阶乘数确定每一位在剩余数字中的位置。
- 更新 k 值:更新
k为k减去前面已确定位的组合数。 - 重复选择数字:直到所有位置都填满。
完整的规范代码
def getPermutation(n, k):"""使用数学方法和减治法获取第k个排列:param n: int, 集合的大小:param k: int, 排列的序号:return: str, 第k个排列"""factorial = [1] * nfor i in range(1, n):factorial[i] = factorial[i - 1] * ik -= 1 # 转换成索引answer = []numbers = list(range(1, n + 1))for i in range(1, n + 1):index = k // factorial[n - i]answer.append(str(numbers.pop(index)))k %= factorial[n - i]return ''.join(answer)# 示例调用
print(getPermutation(3, 3)) # 输出: "213"
print(getPermutation(4, 9)) # 输出: "2314"
算法分析
- 时间复杂度:(O(n^2)),计算阶乘数组为 (O(n)),确定每一位数字为 (O(n^2))(因为每次都要从列表中删除元素)。
- 空间复杂度:(O(n)),存储阶乘数组和数字列表。
方法二:下一个排列法
解题步骤
- 生成最小排列:首先生成
[1,2,...,n]。 - 应用 next permutation:应用
k-1次“下一个排列”算法得到第k个排列。
完整的规范代码
def getPermutation(n, k):"""使用next permutation方法获取第k个排列:param n: int, 集合的大小:param k: int, 排列的序号:return: str, 第k个排列"""def next_permutation(nums):i = j = len(nums) - 1while i > 0 and nums[i-1] >= nums[i]:i -= 1if i == 0: # nums are in descending ordernums.reverse()returnk = i - 1 # find the last "ascending" positionwhile nums[j] <= nums[k]:j -= 1nums[k], nums[j] = nums[j], nums[k] l, r = k+1, len(nums)-1 # reverse the second partwhile l < r:nums[l],nums[r] = nums[r], nums[l]l +=1; r -= 1nums = list(range(1, n + 1))for _ in range(k - 1):next_permutation(nums)return ''.join(map(str, nums))# 示例调用
print(getPermutation(3, 3)) # 输出: "213"
print(getPermutation(4, 9)) # 输出: "2314"
算法分析
- 时间复杂度:(O(n \times k)),每次生成下一个排列需要 (O(n)) 时间。
- 空间复杂度:(O(n)),存储数字列表。
方法三:DFS回溯法
解题步骤
- DFS遍历:使用深度优先搜索遍历所有可能的排列。
- 计数并返回:当遍历到第
k个排列时立即返回。
完整的规范代码
def getPermutation(n, k):"""使用DFS回溯法获取第k个排列:param n: int, 集合的大小:param k: int, 排列的序号:return: str, 第k个排列"""def dfs(path):nonlocal countif len(path) == n:count += 1if count == k:return pathreturnfor number in range(1, n+1):if number in path:continueres = dfs(path + [number])if res:return rescount = 0result = dfs([])return ''.join(map(str, result)) if result else ""# 示例调用
print(getPermutation(3, 3)) # 输出: "213"
print(getPermutation(4, 9)) # 输出: "2314"
算法分析
- 时间复杂度:(O(n!)),理论上需要遍历所有排列。
- 空间复杂度:(O(n)),递归深度为
n。
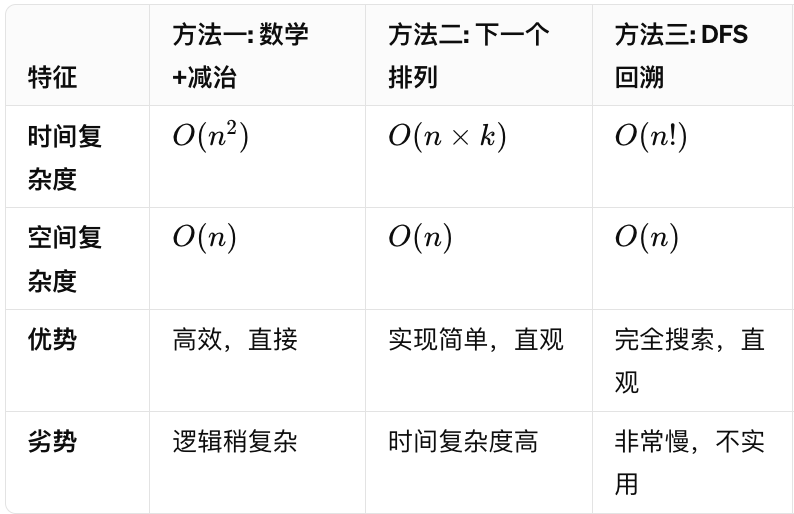
不同算法的优劣势对比
应用示例详解:密码生成系统
场景描述
在密码生成和密码管理软件中,经常需要生成复杂且难以预测的密码来增加安全性。使用“第 k 个排列”算法可以在预定义字符集上生成随机但确定的密码,适用于需要高安全性的应用场景,如在线银行、军事通信等。
方法:数学+减治法
技术选择:
选择方法一(数学+减治法),因为它可以直接计算出第 k 个排列而无需生成所有排列,提高了生成效率和保密性。
实现步骤:
- 选择字符集:定义一个字符集,例如包含大小写字母和数字
[1-9, a-z, A-Z]。 - 计算阶乘:预先计算出所有小于字符集大小的阶乘,用于后续计算排列位置。
- 确定每位字符:根据阶乘和 k 值,快速确定每一位置上的字符,直接计算出第 k 个排列。
- 生成密码:将计算出的排列作为密码,提供给用户或用于加密应用。
代码实现:
def getPermutation(characters, k):"""使用数学方法和减治法基于给定字符集生成密码:param characters: str, 字符集:param k: int, 指定的排列序号:return: str, 生成的密码(排列)"""n = len(characters)factorial = [1] * (n + 1)for i in range(2, n + 1):factorial[i] = factorial[i - 1] * ik -= 1 # 转换为基于0的索引answer = []numbers = list(characters)for i in range(1, n + 1):index = k // factorial[n - i]answer.append(numbers.pop(index))k %= factorial[n - i]return ''.join(answer)# 示例调用
chars = "123456789ABCDEF"
k = 9432
print(getPermutation(chars, k)) # 输出: 第9432个排列
应用优势
- 效率高:直接计算第 k 个排列,无需枚举所有可能,适合实时密码生成需求。
- 安全性强:密码的生成基于数学计算,没有明显的规律,安全性高。
- 适用性广:可根据不同的字符集和需求灵活定制密码生成策略。
总结
通过在密码生成系统中应用“第 k 个排列”算法,开发者可以提供一种高效且安全的方式来生成复杂密码。此外,该算法的高计算效率和确定性也使其成为理想的选择,用于需要快速生成大量密码或密钥的场合,比如动态令牌生成、临时密码分配等。此方法不仅优化了密码生成过程,也极大提高了密码管理系统的整体安全性。
这篇关于python 数学+减治、下一个排列法、DFS回溯法实现:第 k 个排列【LeetCode 题目 60】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




