本文主要是介绍代码随想录算法训练营第四十八天| 198.打家劫舍,213.打家劫舍II,337.打家劫舍III,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目与题解
198.打家劫舍
题目链接:198.打家劫舍
代码随想录题解:198.打家劫舍
视频讲解:动态规划,偷不偷这个房间呢?| LeetCode:198.打家劫舍_哔哩哔哩_bilibili
解题思路:
这道还比较容易,设置dp[i]为偷到第i家的收益,那么,如果要偷第i家,就不偷第i-1家,收益为dp[i-2]+nums[i-1];如果不偷第i家,收益就是偷前i-1家的收益,为dp[i-1]。dp[0]设置为0,表示一家都没有,dp[1]设置为只有第一家存在的情况下的收益,初始化为nums[0]。
class Solution {public int rob(int[] nums) {if (nums.length == 0) return 0;if (nums.length == 1) return nums[0];int[] dp = new int[nums.length + 1];dp[0] = 0;dp[1] = nums[0];for (int i = 2; i <= nums.length; i++) {dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);}return dp[nums.length];}
}看完代码随想录之后的想法
基本思路是一样的,不过为了理解方便,可以保证dp的下标和nums的下标是一一对应的,即dp[0]直接初始化为nums[0]。
因为本题dp[i]只跟dp[i-1]和dp[i-2]相关,可以优化一下空间,只保存前两个数据。
class Solution {public int rob(int[] nums) {if (nums.length == 1) {return nums[0];}// 初始化dp数组// 优化空间 dp数组只用2格空间 只记录与当前计算相关的前两个结果int[] dp = new int[2];dp[0] = nums[0];dp[1] = Math.max(nums[0],nums[1]);int res = 0;// 遍历for (int i = 2; i < nums.length; i++) {res = Math.max((dp[0] + nums[i]) , dp[1] );dp[0] = dp[1];dp[1] = res;}// 输出结果return dp[1];}
}遇到的困难
无
213.打家劫舍II
题目链接:213.打家劫舍II
代码随想录题解:213.打家劫舍II
视频讲解:动态规划,房间连成环了那还偷不偷呢?| LeetCode:213.打家劫舍II_哔哩哔哩_bilibili
解题思路:
一开始想着设置一个robFirst数组,表示偷到当前家的时候第一家是否被偷,来判断最后一家是否能偷,即dp的最后一个数是否要取到nums[i],但是写起来很复杂,而且还有涉及到万一前后两家价值一样是怎么表示要不要偷第一家的情况,容易混乱,最后还是看答案了。
看完代码随想录之后的想法
方法很单纯,这里学习一下环形题的处理方法。
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素
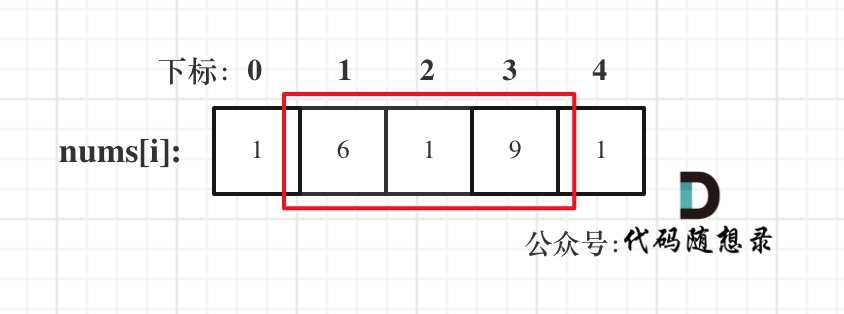
- 情况二:考虑包含首元素,不包含尾元素
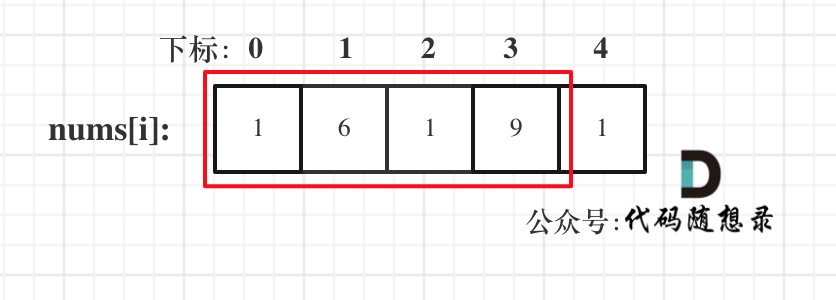
- 情况三:考虑包含尾元素,不包含首元素
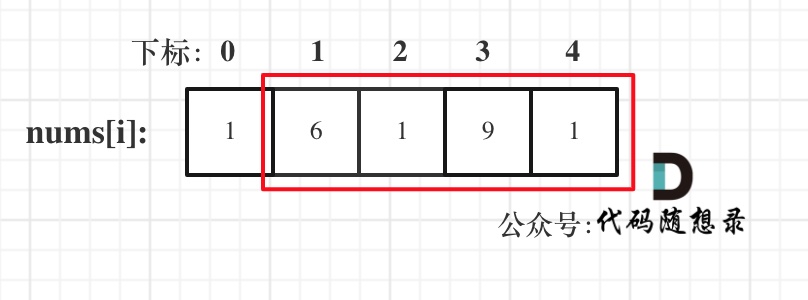
注意我这里用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
所以对于这道题,只要分两类,就可以直接套用前一题的打家劫舍方法:求0-nums.length-2的数组中打家劫舍的最优结果,以及求1-nums.length-1数组中最优结果,就不存在环的问题了。
写的时候要注意数组始末点和遍历始末点是有关系的,不要写错。
class Solution {public int rob(int[] nums) {if (nums.length == 0) return 0;if (nums.length == 1) return nums[0];return Math.max(robRange(nums, 0, nums.length-2), robRange(nums, 1, nums.length-1));}public int robRange(int[] nums, int start, int end) {if (end == start) return nums[start];int[] dp = new int[nums.length];dp[start] = nums[start];dp[start + 1] = Math.max(nums[start], nums[start+1]);for (int i = start + 2; i <= end; i++) {dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);}return dp[end];}
}遇到的困难
结果的想法很单纯也很巧妙,写的复杂的时候就要思考一下是不是想错了。
337.打家劫舍III
题目链接:337.打家劫舍III
代码随想录题解:337.打家劫舍III
视频讲解:动态规划,房间连成树了,偷不偷呢?| LeetCode:337.打家劫舍3_哔哩哔哩_bilibili
解题思路:
总体思路是差不多的,如果偷了当前节点的,就不偷其左右子树,反之则偷左右子树,计算左右之和即可。
方法主要采取递归的方式,可以用后序遍历,分两种情况:如果偷了当前节点,则计算三者之和:当前节点的值,其左节点的左右节点可偷最大值,其右节点的左右节点可偷最大值;如果不偷当前节点,则计算左节点可偷最大值和右节点可偷最大值之和。比较这两种情况下的最大值,返回即可。
但是这个方法它超时了,因为这里计算了root的四个孙子(左右孩子的孩子)为头结点的子树的情况,又计算了root的左右孩子为头结点的子树的情况,计算左右孩子的时候其实又把孙子计算了一遍。于是看答案。
class Solution {public int rob(TreeNode root) {if (root == null) return 0;if (root.left == null && root.right == null)return root.val;// 偷根节点int result1 = root.val;if (root.left != null) {result1 += rob(root.left.left) + rob(root.left.right);}if (root.right != null) {result1 += rob(root.right.left) + rob(root.right.right);}// 不偷根节点int result2 = rob(root.left) + rob(root.right);int result = Math.max(result1, result2);map.put(root, result);return result;}
}看完代码随想录之后的想法
随想录给出了两种解法,一种还是递归,但是优化版。它设置了一个map用于记录当前节点的值是否被统计过,如果统计了就不用重复递归计算了,直接返回就行。
class Solution {Map<TreeNode, Integer> map = new HashMap<>();public int rob(TreeNode root) {if (root == null) return 0;if (root.left == null && root.right == null)return root.val;if (map.containsKey(root)) return map.get(root);// 偷根节点int result1 = root.val;if (root.left != null) {result1 += rob(root.left.left) + rob(root.left.right);}if (root.right != null) {result1 += rob(root.right.left) + rob(root.right.right);}// 不偷根节点int result2 = rob(root.left) + rob(root.right);int result = Math.max(result1, result2);map.put(root, result);return result;}
}另一种则是用动态规划来做,每个节点都用一个大小为2的数组,分别记录不偷该节点和偷该节点可获得的最大值,利用递归时候的栈来依次记录每个节点的dp。递归函数首先计算当前节点左节点和右节点的dp,如果不偷root,其dp[0]为二者之和:偷左节点resultLeft[1]与不偷左节点resultLeft[0]的最大值,偷右节点resultRight[1]与不偷右节点resultRight[0]的最大值;如果偷root,其dp[1]为不偷左节点resultLeft[0]和不偷右节点resultRight[0]的二者之和。
class Solution {public int rob(TreeNode root) {int[] resultRoot = robTree(root);return Math.max(resultRoot[0], resultRoot[1]);}public int[] robTree(TreeNode root) {if (root == null) return new int[]{0,0};int[] resultNode = new int[2];int[] resultLeft = robTree(root.left);int[] resultRight = robTree(root.right);// 偷rootresultNode[1] = root.val + resultLeft[0] + resultRight[0];// 不偷rootresultNode[0] = Math.max(resultLeft[0], resultLeft[1]) + Math.max(resultRight[0], resultRight[1]);return resultNode;}
}遇到的困难
超时的时候要思考一下超时的根本原因,然后看看是否能够剪枝去掉重复计算。树也可以用map来用空间换时间,学到了。
还有就是树也是可以用dp的,不过这里的dp不用一次性记录每一个节点的结果,相当于是滚动更新了,对于二叉树而言,也只有这样的更新方法。
今日收获
学习了一下不同限制条件下dp的计算方式,都很巧妙,好难想,努力记住。
这篇关于代码随想录算法训练营第四十八天| 198.打家劫舍,213.打家劫舍II,337.打家劫舍III的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



