本文主要是介绍后缀数组一·重复旋律,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。
旋律是一段连续的数列,相似的旋律在原数列可重叠。比如在1 2 3 2 3 2 1 中 2 3 2 出现了两次。
怎么知道一段旋律中出现次数至少为K次的旋律最长是多少?
输入
第一行两个整数 N和K。1≤N≤20000 1≤K≤N
接下来有 N 个整数,表示每个音的数字。1≤数字≤100
输出
一行一个整数,表示答案。
8 2 1 2 3 2 3 2 3 1
4解法提示:
这次的问题被称为最长可重叠重复K次子串问题。
顾名思义,后缀数组就是记录所有后缀的数组,同时,它也是有序的。后缀数组 SA 可以帮助我们解决单字符串问题、两个字符串的问题和多个字符串的问题等。
比如说字符串banana$,我们暂且把$认为是一个字符(表示字符串结尾)。我们记suffix(i)表示从原字符串第i个字符开始到字符串结尾的后缀。我们把它所有的后缀拿出来按字典序排序:
| 后缀 | i |
|---|---|
| $ | 7 |
| a$ | 6 |
| ana$ | 4 |
| anana$ | 2 |
| banana$ | 1 |
| na$ | 5 |
| nana$ | 3 |
并且我们把排好序的数组记做sa。比如sa[1]=7,sa[4]=2。
另外,后缀数组会顺便记录名次数组 Rank, Rank[i] 保存的是后缀 i 在所有后缀中从小到大排列的“名次”。比如上个字符串中Rank[7]=1,Rank[4]=3
我们现在令 height[i] 是 suffix(sa[i-1]) 和 suffix(sa[i]) 的最长公共前缀长度,即排名相邻的两个后缀的最长公共前缀长度。比如height[4]就是anana$和ana$的最长公共前缀,也就是ana,长度为3。你注意,这个height数组有一个神奇的性质:若 rank[j] < rank[k],则后缀 Sj..n 和 Sk..n 的最长公共前缀为 min{height[rank[j]+1],height[rank[j]+2]...height[rank[k]]}。这个性质是显然的,因为我们已经后缀按字典序排列。
我们有如下结论:height[rank[i]] ≥ height[rank[i-1]]-1。
设suffix(k)是排在suffix(i-1)前一名的后缀,则它们的最长公共前缀是height[rank[i-1]]。那么suffix(k+1)将排在suffix(i)的前面(这里要求height[rank[i-1]]>1,如果height[rank[i-1]]≤1,原式显然成立)并且suffix(k+1)和suffix(i)的最长公共前缀是height[rank[i-1]]-1,所以suffix(i)和在它前一名的后缀的最长公共前缀至少是height[rank[i-1]]-1。
这样我们按照 height[rank[1]], height[rank[2]] ... height[rank[n]] 的顺序计算,利用height数组的性质,就可以将时间复杂度可以降为 O(n)。这是因为height数组的值最多不超过n,每次计算结束我们只会减1,所以总的运算不会超过2n次。
有了height,求最长可重叠重复K次子串就方便了。重复子串即两后缀的公共前缀,最长重复子串,等价于两后缀的最长公共前缀的最大值。问题就转化成了,求height 数组中最大的长度为 K的子序列的最小值。
后缀数组的求法有很多,最有名的是两种倍增算法和DC算法。时间复杂度上DC算法更优,但是很复杂。我们这里只介绍相对容易的倍增算法。
简单来说,倍增算法分以下四步
- 对长度为 20=1 的字符串,也就是所有单字母排序。
- 用长度为 20=1 的字符串,对长度为 21=2 的字符串进行双关键字排序。考虑到时间效率,我们一般用基数排序。
- 用长度为 2k-1 的字符串,对长度为 2k 的字符串进行双关键字排序。
- 直到 2k ≥ n,或者名次数组 Rank 已经从 1 排到 n,得到最终的后缀数组。
以字符串 "aabaaaab" 为例, 整个过程如图所示。 其中 x、 y 是表示长度为 2k 的字符串的两个关键字。
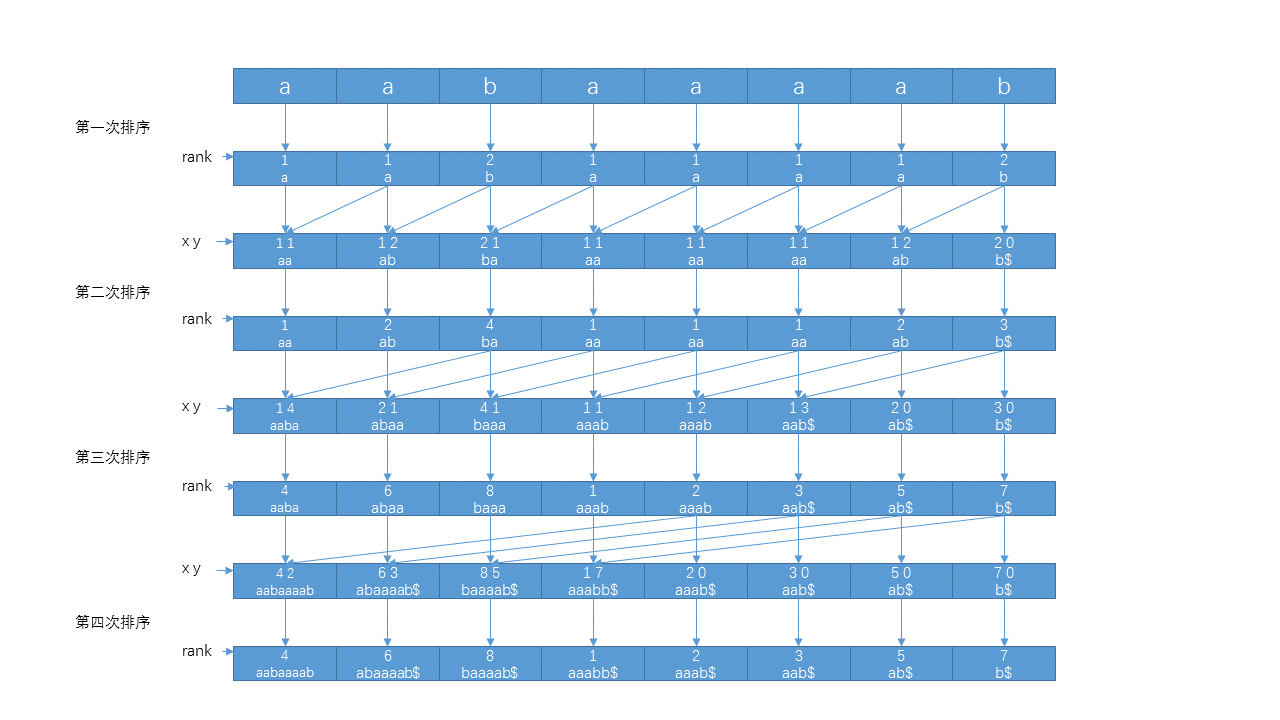
感觉这个算法就是利用已用的后缀排序信息来更新更长串的排序信息。
其实height数组表示所有后缀排序后,每个后缀字符串与前一个的最长公共前缀,所以height中最大值可以看做重复两次的字符串的最长长度(可以重叠),如果继续对height数组相邻项取最小值,其中最大值就表示重复三次的字符串的最长长度,所以求重复k次的最长长度,就可以重复k-1次取相邻的最小值,再求最大值。
关于后缀数组的详细解说,请参考
http://blog.csdn.net/yxuanwkeith/article/details/50636898
先提供我一开始的简单实现,效率比较低:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <map>
#include <algorithm>
#define MAX 20010
using namespace std;//FILE *stream;
int N, K;
string s, c;
int SA[MAX];//后缀数组,保存排序后后缀字符串的开头位置,本身下标对应名次
int RANK[MAX];//名次数组,保存排序后后缀字符串名次,本身下标对应字符串开头位置
int HEIGHT[MAX];//排名相邻的两个后缀的最长公共前缀
map<string, int>m;
void solve()
{int i, j;int index;m.clear();for (i = 1; i < N; ++i)m.insert(make_pair(s.substr(i, N - i), i));auto it = m.begin();for (i = 1; it != m.end(); ++it, ++i){index = it->second;SA[i] = index;RANK[N - it->first.length()] = i;}for (i = 1, j = 0; i <= N; i++){if (j) j--;while (s[i + j] == s[SA[RANK[i] - 1] + j]) j++;HEIGHT[RANK[i]] = j;}int maxLen = -1;while (K-- > 1){maxLen = -1;for (i = N - 1; i > 1; --i){if (maxLen < HEIGHT[i])maxLen = HEIGHT[i];if (K>1)HEIGHT[i] = min(HEIGHT[i], HEIGHT[i - 1]);}}cout << maxLen << endl;
}
int main()
{//freopen_s(&stream, "in.txt", "r", stdin);int i;cin >> N >> K;s = "#";for (i = 0; i < N; ++i){cin >> c;getchar();s += c;}N++;if (K > 1)solve();elsecout << N - 1 << endl;//freopen_s(&stream, "CON", "r", stdin);//system("pause");return 0;
}较高效的倍增法,但是比较难理解,而且利用的中间数组比较多,易弄错,不过可以拿过来用:
const int N = 100000 + 50;//后续的规模更大,体现倍增法的优势
int SA[N];//后缀数组,保存排序后后缀字符串的开头位置,本身下标对应名次
int RANK[N];//名次数组,保存排序后后缀字符串名次,本身下标对应字符串开头位置
int HEIGHT[N];//排名相邻的两个后缀的最长公共前缀
int wa[N], wb[N], wss[N], wv[N];
int aa[N];
int n;int cmp(int *r, int a, int b, int l)
{return (r[a] == r[b]) && (r[a + l] == r[b + l]);
}void getSA(int *r, int *sa, int n, int m)//r[]为初始输入,可以对应改为字符串数组,sa[]为后缀数组,n为输入个数+1,m为输入中的最大值,字符的话可以对应改为ascii码最大值
{int i, j, p, *x = wa, *y = wb, *t;for (i = 0; i<m; i++) wss[i] = 0;for (i = 0; i<n; i++) wss[x[i] = r[i]]++;for (i = 1; i<m; i++) wss[i] += wss[i - 1];for (i = n - 1; i >= 0; i--) sa[--wss[x[i]]] = i;for (j = 1, p = 1; p<n; j *= 2, m = p){for (p = 0, i = n - j; i<n; i++) y[p++] = i;for (i = 0; i<n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;for (i = 0; i<n; i++) wv[i] = x[y[i]];for (i = 0; i<m; i++) wss[i] = 0;for (i = 0; i<n; i++) wss[wv[i]]++;for (i = 1; i<m; i++) wss[i] += wss[i - 1];for (i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i]; //基数排序部分for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i<n; i++)x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;}
}void getHeight(int *r, int n)
{int i, j, k = 0;for (i = 1; i <= n; i++) RANK[SA[i]] = i;for (i = 0; i<n; HEIGHT[RANK[i++]] = k)for (k ? k-- : 0, j = SA[RANK[i] - 1]; r[i + k] == r[j + k]; k++);
}//输入aa[0]-aa[n-1]
//getSA(aa,SA,n+1,105); //注:此处计算出的为SA[1]-SA[n],而且每个SA值表示的是下标,从0-n-1
//getHeight(aa,n); //注:此处计算出的为HEIGHT[1]-HEIGHT[n]
这篇关于后缀数组一·重复旋律的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






