本文主要是介绍《算法导论》实验四:哈夫曼(Huffman)编码问题(C++实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、题目描述
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0,1串表示各字符的最优表示方式。一个包含100,000个字符的文件,各字符出现频率不同,如下表所示:
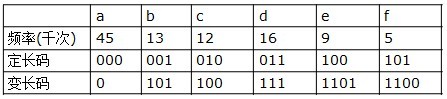
有多种方式表示文件中的信息,若用0,1码表示字符的方法,即每个字符用唯一的一个0,1串表示。若采用定长编码表示,则需要3位表示一个字符,整个文件编码需要300,000位;若采用变长编码表示,给频率高的字符较短的编码;频率低的字符较长的编码,达到整体编码减少的目的,则整个文件编码需要(45×1+13×3+12×3+16×3+9×4+5×4)×1000=224,000位,由此可见,变长码比定长码方案好,总码长减小约25%。
二、算法设计与分析
1、前缀码:
对每一个字符规定一个0,1串作为其代码,并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单;例如001011101可以唯一的分解为0,0,101,1101,因而其译码为aabe。
译码过程需要方便的取出编码的前缀,因此需要表示前缀码的合适的数据结构。为此,可以用二叉树作为前缀码的数据结构:树叶表示给定字符;从树根到树叶的路径当作该字符的前缀码;代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。
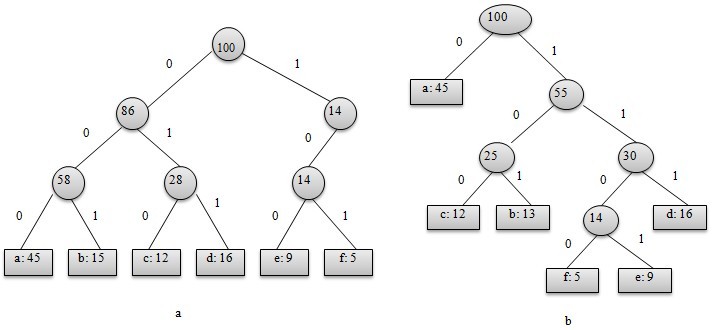
图-1a 与固定长度编码对应的树; 图-1b 对应于最优前缀编码的树
从上图可以看出,表示最优前缀码的二叉树总是一棵完全二叉树,即树中任意节点都有2个儿子。图a表示定长编码方案不是最优的,其编码的二叉树不是一棵完全二叉树。在一般情况下,若C是编码字符集,表示其最优前缀码的二叉树中恰有|C|个叶子。每个叶子对应于字符集中的一个字符,该二叉树有|C|-1个内部节点。
给定编码字符集C及频率分布f,即C中任一字符c以频率f(c)在数据文件中出现。C的一个前缀码编码方案对应于一棵二叉树T。字符c在树T中的深度记为dT(c)。dT(c)也是字符c的前缀码长。则平均码长定义为:
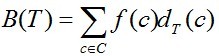
使平均码长达到最小的前缀码编码方案称为C的最优前缀码。
2、构造哈夫曼编码:
哈夫曼提出构造最优前缀码的贪心算法,由此产生的编码方案称为哈夫曼编码。其构造步骤如下:
(1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
(2)算法以|C|个叶结点开始,执行|C|-1次的“合并”运算后产生最终所要求的树T。
(3)假设编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后,产生一棵新的树,其频率为合并的2棵树的频率之和,并将新树插入优先队列Q。经过n-1次的合并后,优先队列中只剩下一棵树,即所要求的树T。
构造过程如图-2所示:
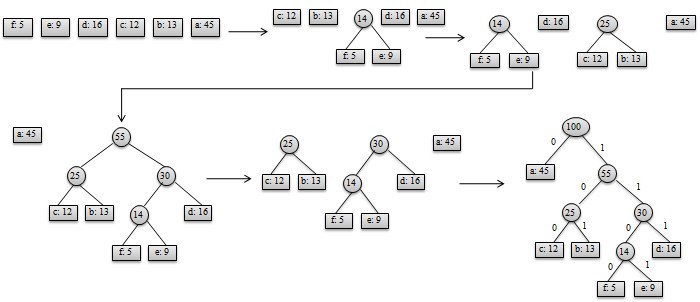
图-2 哈夫曼树构造过程
三、结果与分析
本实验以算法导论书中的例题为测试用例,来验证算法的正确性。即
实验结果截图如下图-7,结果与题目描述中给出的变长代码字一样:
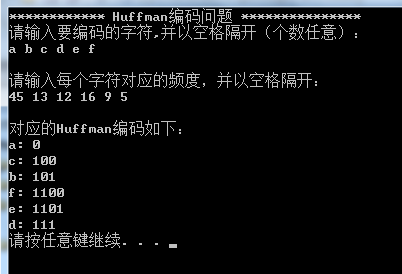
图-7 实验结果截图
四、实验总结
1、实验结果与给出的变长代码字一样,算法正确,且哈夫曼编码问题是一个贪心算法问题。采用哈夫曼编码技术可以最小化总的编码长度,从而实现数据文件的压缩存储。
2、构造好哈夫曼树后,可用排列树回溯法来打印哈夫曼编码,即遇到左子树向左走,vector添加记录0;遇到右子树向右走,vector添加记录1;走到叶子节点并打印出叶节点的编码后回溯,同时往上退一层,则vector弹出一个值。如此不断回溯下去,即可打印所有字符编码。
五、源代码(C++)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;//Huffman树的节点类
typedef struct Node
{char value; //结点的字符值 int weight; //结点字符出现的频度Node *lchild,*rchild; //结点的左右孩子
}Node;//自定义排序规则,即以vector中node结点weight值升序排序
bool ComNode(Node *p,Node *q)
{return p->weight<q->weight;
}//构造Huffman树,返回根结点指针
Node* BuildHuffmanTree(vector<Node*> vctNode)
{while(vctNode.size()>1) //vctNode森林中树个数大于1时循环进行合并{sort(vctNode.begin(),vctNode.end(),ComNode); //依频度高低对森林中的树进行升序排序Node *first=vctNode[0]; //取排完序后vctNode森林中频度最小的树根Node *second=vctNode[1]; //取排完序后vctNode森林中频度第二小的树根Node *merge=new Node; //合并上面两个树merge->weight=first->weight+second->weight;merge->lchild=first;merge->rchild=second;vector<Node*>::iterator iter;iter=vctNode.erase(vctNode.begin(),vctNode.begin()+2); //从vctNode森林中删除上诉频度最小的两个节点first和secondvctNode.push_back(merge); //向vctNode森林中添加合并后的merge树}return vctNode[0]; //返回构造好的根节点
}//用回溯法来打印编码
void PrintHuffman(Node *node,vector<int> vctchar)
{if(node->lchild==NULL && node->rchild==NULL){//若走到叶子节点,则迭代打印vctchar中存的编码cout<<node->value<<": ";for(vector<int>::iterator iter=vctchar.begin();iter!=vctchar.end();iter++)cout<<*iter;cout<<endl;return;}else{vctchar.push_back(1); //遇到左子树时给vctchar中加一个1PrintHuffman(node->lchild,vctchar);vctchar.pop_back(); //回溯,删除刚刚加进去的1vctchar.push_back(0); //遇到左子树时给vctchar中加一个0PrintHuffman(node->rchild,vctchar);vctchar.pop_back(); //回溯,删除刚刚加进去的0}
}int main()
{cout<<"************ Huffman编码问题 ***************"<<endl;cout<<"请输入要编码的字符,并以空格隔开(个数任意):"<<endl;vector<Node*> vctNode; //存放Node结点的vector容器vctNodechar ch; //临时存放控制台输入的字符while((ch=getchar())!='\n'){if(ch==' ')continue; //遇到空格时跳过,即没输入一个字符空一格空格Node *temp=new Node;temp->value=ch;temp->lchild=temp->rchild = NULL;vctNode.push_back(temp); //将新的节点插入到容器vctNode中}cout<<endl<<"请输入每个字符对应的频度,并以空格隔开:"<<endl;for(int i=0;i<vctNode.size();i++)cin>>vctNode[i]->weight;Node *root = BuildHuffmanTree(vctNode); //构造Huffman树,将返回的树根赋给rootvector<int> vctchar;cout<<endl<<"对应的Huffman编码如下:"<<endl;PrintHuffman(root,vctchar);system("pause");
}这篇关于《算法导论》实验四:哈夫曼(Huffman)编码问题(C++实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







