代码随想录算法训练营第三十八天|509. 斐波那契数，70.爬楼梯，746. 使用最小花费爬楼梯

本文主要是介绍代码随想录算法训练营第三十八天|509. 斐波那契数，70.爬楼梯，746. 使用最小花费爬楼梯，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

动态规划(DP)

如果某一问题有很多重叠子问题，使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的

一、动态规划包含哪些问题？

1、基础问题，如斐波那契数
2、背包问题，很经典的问题
3、打家劫舍
4、股票问题
5、子序列问题，如最长子序列，编辑距离等

二、动态规划的解题步骤

1、确定dp数组（dp table）以及下标的含义，用dp数组来保存递归的结果
2、确定递推公式（核心）
3、dp数组如何初始化
4、确定遍历顺序
5、举例推导dp数组

509. 斐波那契数

斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2），其中 n > 1给你n ，请计算 F(n)。

在这里插入图片描述

题目链接/讲解链接：
https://programmercarl.com/0509.%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0.html

思路

按照动态规划五部曲来解题。
1、确定dp数组及下标的含义。dp[i]表示：第i个数的斐波那契数值为dp[i]
2、确定递归公式。本题给出条件：F(n) = F(n -1) + F(n -2），其中 n > 1，
所以递归公式就是dp[i] = dp[i -1] + dp[i -2]
3、初始化dp数组。本题也以给出：dp[0] = 0，dp[1] = 1
4、确定遍历的顺序。从递归公式dp[i] = dp[i -1] + dp[i -2];中可以看出，dp[i]是依赖 dp[i -1]和dp[i -2]，那么遍历的顺序一定是从前到后遍历的
5、举例推导dp数组。这是一个验证的过程，例如当n为10的时候，dp数组应该是如下的数列：
0 1 1 2 3 5 8 13 21 34 55

解题

class Solution {
public:int fib(int n) {if (n <= 1) return n;vector<int> dp(n + 1);//0-n是有n+1个数dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};

70.爬楼梯

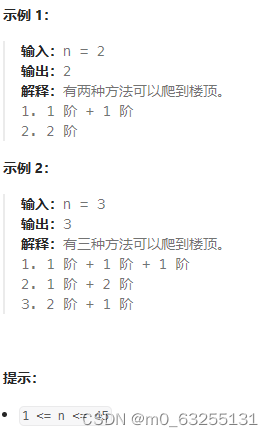
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬1或2个台阶。
你有多少种不同的方法可以爬到楼顶呢？注意：给定 n是一个正整数。

在这里插入图片描述

题目链接/讲解链接：
https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF.html

思路

动态规划五部曲。
1、确定dp数组和下标的含义。dp[i]表示：到达第i阶楼梯有dp[i]种方法。
2、确定递归公式。
dp[i]可以有两个方向推出来。
首先是dp[i -1]，上i-1层楼梯，有dp[i -1]种方法，那么再一步跳一个台阶就是dp[i]；
还有就是dp[i-2]，上i-2层楼梯，有dp[i-2]种方法，那么再一步跳两个台阶也是dp[i]。
那么dp[i]就是 dp[i-1]与dp[i-2]之和。
所以递归公式为dp[i] = dp[i-1] + dp[i-2]。
3、初始化dp数组。
在我看来，题目中的条件：1 <= n <= 45，就不需要考虑dp[0]的情况，直接初始化dp[1]和dp[2]：
dp[1]=1，dp[2]=2。
4、确定遍历的顺序。从前往后
5、举例推导dp数组。

解题

class Solution {
public:int climbStairs(int n) {if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) { // 注意i是从3开始的dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};

题目：746. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i]是从楼梯第 i个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为0或下标为1的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

在这里插入图片描述

题目链接/讲解链接：
https://programmercarl.com/0746.%E4%BD%BF%E7%94%A8%E6%9C%80%E5%B0%8F%E8%8A%B1%E8%B4%B9%E7%88%AC%E6%A5%BC%E6%A2%AF.html

思路

五部曲：
1、确定dp数组和下标的含义。
dp[i]表示：爬到第i个台阶的最低花费是dp[i]。
2、确定递推公式。
我们如何可以到达第i个台阶？
有两种方式：
可以从第i-1个台阶往上爬一个台阶到第i个台阶，花费的总体力为从开始到达第i-1个台阶的dp[i-1]加上从第i-1个台阶爬到第i个台阶花费的体力cost[i-1]；
还可以从第i-2个台阶往上爬两个台阶到第i个台阶，花费的总体力为从开始到达第i-2个台阶的dp[i-2]加上从第i-2个台阶爬到第i个台阶花费的体力cost[i-1]；
dp[i]是最低花费，所以可以得到递归公式为：

dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])

3、初始化dp数组。
看一下递归公式，dp[i]由dp[i-1]，dp[i-2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]和dp[1]推出。

那么 dp[0]应该是多少呢？
题目描述中说了“你可以选择从下标为0或下标为1的台阶开始爬楼梯。” 也就是第0个台阶或者第1个台阶是不花费的，但从第0个台阶或者第1个台阶往上跳的话，需要花费 cost[0]或者cost[1]。
所以初始化 dp[0] = 0，dp[1] = 0
4、确定遍历顺序。从前往后。
5、举例推导dp数组。如下图：
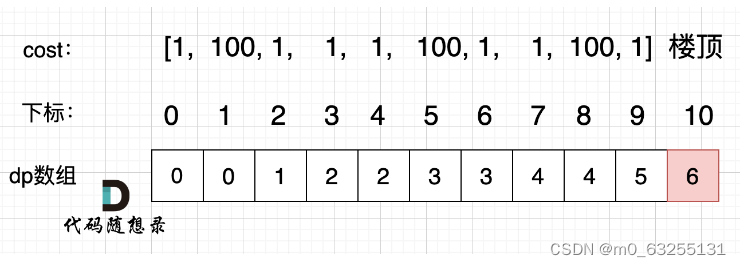
在这里插入图片描述

解题

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1);//我们最终到达的是楼顶，楼顶的位置是在cost数组的外面，因此要比cost数组大//初始化dp数组，我们可以选择从0或者1号楼梯开始爬，因此我们到达0或者1号楼梯是不需要花费体力的，cost[0]和cost[1]表示的是已经站在0或者1号楼梯楼了，往上爬需要花费的体力dp[0]=0;dp[1]=0;for(int i =2;i<=cost.size();i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};