Games101 作业一构建模型变换，和透视投影矩阵

本文主要是介绍Games101 作业一构建模型变换，和透视投影矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

知识总结：变换的流程
（1）模型(Model)变换，pa中模型只绕z轴旋转
（2）视图(View)变换，作用是调整摄像机的位置
（3）投影(Projection)变换，pa中要求是透视投影，透视投影可看成挤压 + 正交变换
（4）视口(Viewport)变换，将投影变换所得的[-1,1]²变换到屏幕空间
在这里插入图片描述

代码分析：
（1）获得视图变换矩阵（main.cpp）
视图变换的作用是移动摄像机，可看成是物体的反向移动

Eigen::Matrix4f get_view_matrix(Eigen::Vector3f p/;eye_pos)
{Eigen::Matrix4f view = Eigen::Matrix4f::Identity();//4*4单位矩阵Eigen::Matrix4f translate;translate << 1, 0, 0, -eye_pos[0], 0, 1, 0, -eye_pos[1], 0, 0, 1,-eye_pos[2], 0, 0, 0, 1;//得到效果和摄像机移动方向相反的矩阵view = translate * view;return view;
}

（2）模型变换矩阵，效果是使模型绕z轴旋转

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{Eigen::Matrix4f model = Eigen::Matrix4f::Identity();// TODO: Implement this function// Create the model matrix for rotating the triangle around the Z axis.// Then return it.Eigen::Matrix4f R;R << cos(rotation_angle),sin(rotation_angle), 0, 0,sin(rotation_angle), cos(rotation_angle), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1;return R;return model;
}

（3）构建透视投影矩阵
光看课程还有很多细节没太清楚…包括get_projection_matrix这个函数的参数是什么意思pdf上也没有解释…图形学新手废了好大劲，主要参考了一个大佬的文章
参考文章
总之，透视投影可看成是挤压 + 正交投影（平移+缩放）
难度集中在挤压矩阵persp2ortho的构建上，为此需要注意：
1、近平面上的点都x,y,z都不会变 2、远平面上的点z不会变
其余的点遵循相似三角形的原理，解方程组可得到矩阵
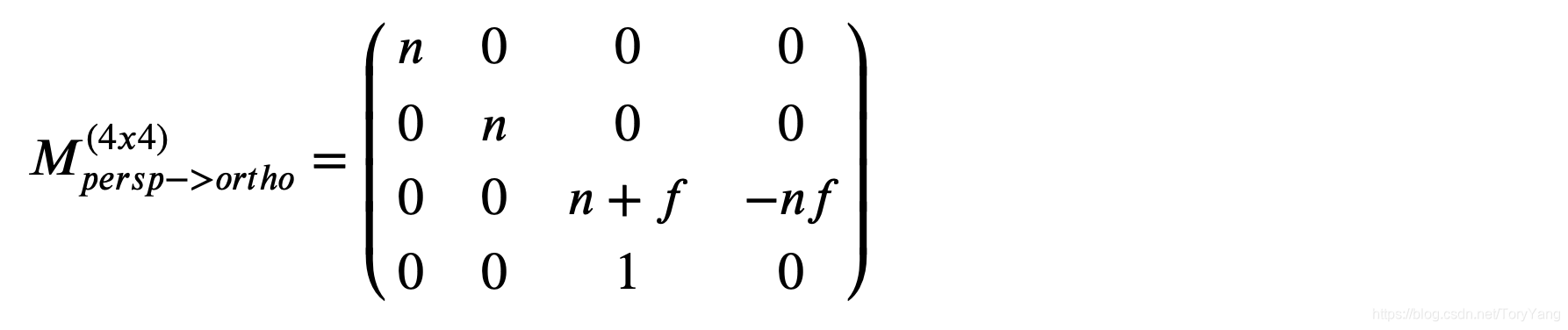
在这里插入图片描述

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)
{Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();Eigen::Matrix4f persp2ortho = Eigen::Matrix4f::Identity();persp2ortho << zNear, 0, 0, 0,0, zNear, 0, 0,0, 0, zNear + zFar, -zNear * zFar,0, 0, 1, 0;double halfEyeRadian = eye_fov * MY_PI / 2 / 180.0;double top = zNear * tan(halfEyeRadian);double bottom = -top;double right = top * aspect_ratio;double left = -right;Eigen::Matrix4f orthoScale = Eigen::Matrix4f::Identity();orthoScale << 2 / (right - left), 0, 0, 0,0, 2 / (top - bottom), 0, 0,0, 0, 2 / (zNear - zFar), 0,0, 0, 0, 1;Eigen::Matrix4f orthoTrans = Eigen::Matrix4f::Identity();orthoTrans << 1, 0, 0, -(right + left) / 2,0, 1, 0, -(top + bottom) / 2,0, 0, 1, -(zNear + zFar) / 2,0, 0, 0, 1;Eigen::Matrix4f matrixOrtho = orthoScale * orthoTrans;projection = matrixOrtho * persp2ortho;return projection;
}