2024年华中杯B题论文发布+数据预处理问题一代码免费分享

本文主要是介绍2024年华中杯B题论文发布+数据预处理问题一代码免费分享，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【腾讯文档】2024年华中杯B题资料汇总

https://docs.qq.com/doc/DSExMdnNsamxCVUJt

行车轨迹估计交通信号灯周期问题

摘要

在城市化迅速发展的今天，交通管理和优化已成为关键的城市运营问题之一。本文将基于题目给出的数据，对行车轨迹估计交通信号灯周期问题进行研究。

针对问题一，固定周期信号灯周期估计。首先，对于给出的数据进行数据清洗，先进行异常值与缺失值的判定，结合实际情况进行人为判定，结果发现基本不存在这方面的数据问题。因此，基于数据本身对X轴数据、Y轴数据进行综合分析。得出不同的道路类型可能存在同向或异向的道路。因此，对Y轴数据进行肘部法则的聚类分析进行道路分类，对X轴数据位移变化判定方向。基于判定的结果，利用欧氏距离计算每一点的速度，速度为0，标记该时间点车辆为停止状态。提取停止和启动时间，计算持续时间。利用峰值分析，反映红灯时长；计算两个连续停止事件之间的时间差，估算绿灯时长，通过剔除策略排除极端值，保留正常范围内的数据，以确保评估的准确性。

针对问题二，影响因素分析与误差建模。采用问题一想用的数据处理方式，使用肘部法则进行聚类分析，对处理后的数据，引入问题一模型进行评估。对于误差分析，不同的样本车辆比例，选择不同的样本率导入模型进行评估，得出随着样本车辆比例的增加，平均红灯持续时间也呈现增长的趋势等结论。对于不同定位分析，设置偏移量是基于原始坐标的标准差的一定百分比（5%），结果发现并没有引起变化，这也验证的模型能够很好的应对定位不准确问题。

针对问题三，动态周期变化检测。利用问题一二思路计算有效的停车持续时间数据，使用峰值分析确定停车持续时间中的主要峰值，将停车持续时间大于平均值的数据视为有效数据，低于平均值的视为异常值并剔除。使用CUSUM方法判定周期变化点。针对问题四，对新的数据集进行评估。首先，利用给出的数据绘制车辆轨迹图，发现车辆大致为八个方向，因此使用python进行对数据进行分类。对分类后的数据集，采用问题一二三构建模周期模型。

关键词：数据清洗，聚类分析，肘部法则，动态周期变化检测，CUSUM方法

26页 1.2万字（无附录）

无水印照片17页

利用matlab的find函数，对给出的附件一A1、A2、A3、A4、A5数据进行判定，得出并无缺失值。在利用K-S检验判定分布方式，对正态分布数据使用3西格玛原则判定异常值；对非正态分布数据使用箱型图判定异常值。

X轴位置分析

为了更加直观的展示运动轨迹，以ID313、ID150、ID364为例，绘制了其X轴的运动轨迹

图1：轨迹图

Y轴位置分析

对于Y轴的数据，表示横向位置。即道路位置，表示了具体存在几个车道。对于A1数据，可以认为A1为双向车道。

表1：Y值计数

y	计数
1.6	2324
4.8	9328

对于A2等数据文件，发现一共存在4618种y值位置。因此，不可能存在4618条道路。需要基于题目数据进行分类分析。

表1：Y值计数

y	计数
-54.76	1
-54.71	1
-54.67	1
-54.63	1

为了直观的展示Y的具体数值，绘制了概率密度图如下所示

根据y的分布图可以看出，数据集中在特定的几个值上，这可能表示不同的车道位置。使用K-Means聚类算法来尝试确定车道数目。因此，对于这种的聚类方式，我选择与其高度相似的层次聚类算法。层次聚类算法即为开始就将每个数据点视为一个单一的聚类，然后依次合并（或聚集）类，直到所有类合并成一个包含所有数据点的单一聚类。

下面为了更好的解释这一概念，将利用matlab绘制示意图详细的解释这一

通过该图个图，可以看出k=5进行聚类，以识别五个可能的车道位置，并对数据进行聚类。

同时，利用x坐标（位移）随时间的变化判定是否为同一方向，问题一五个附件结果如下所示

图1：绿灯分布图

表 1：路口A1-A5 各自一个方向信号灯周期识别结果

路口	A1	A2	A3	A4	A5
红灯时长（秒）	55.96	44.69	57.08	46.55	51.63

5.4 模型的应用

5.4.1 路口方向划分

利用给出的数据进行路口的划分，需要根据车辆在路口的运动模式或方向来分类数据。这种分类可能需要根据车辆的位置变化（即坐标变化）来确定其可能的方向。

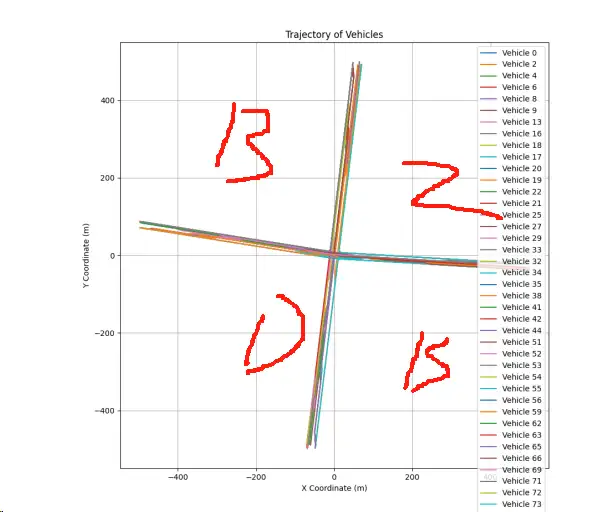
观察车辆轨迹：通过观察车辆坐标随时间的变化，可以推测车辆的大致行驶方向

计算方向：通过计算连续坐标点之间的变化，可以估计车辆的行驶方向。例如，如果x坐标随时间增加而y坐标减少，车辆可能是向东北方向行驶。

首先展示几个车辆的轨迹图，如下图所示

import pandas as pd# Load the data from the uploaded CSV file
file_path = 'A5.csv'
data = pd.read_csv(file_path)# Display the first few rows of the dataframe
data.head(), data.describe()
import matplotlib.pyplot as plt
import seaborn as sns# Plotting the distribution of y values to estimate lanes
plt.figure(figsize=(10, 6))
sns.histplot(data['y'], bins=50, kde=True)
plt.title('Distribution of Lateral Position (y)')
plt.xlabel('Lateral Position (y)')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()
from sklearn.cluster import KMeans
import numpy as np# Determining the optimal number of clusters (lanes)
y_data = data['y'].values.reshape(-1, 1)
sse = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=0).fit(y_data)sse.append(kmeans.inertia_)# Plotting the SSE to find the elbow, which might indicate the optimal k (number of lanes)
plt.figure(figsize=(10, 6))
plt.plot(range(1, 11), sse, marker='o')
plt.title('Elbow Method For Optimal k')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Sum of squared errors (SSE)')
plt.grid(True)
plt.show()# Applying K-Means with k=5
kmeans = KMeans(n_clusters=5, random_state=0).fit(y_data)
centers = kmeans.cluster_centers_# Plotting the clusters
plt.figure(figsize=(10, 6))
sns.scatterplot(x=data['x'], y=data['y'], hue=kmeans.labels_, palette='viridis', s=30)
plt.scatter(centers[:, 0], centers[:, 0], c='red', s=200, alpha=0.75, marker='X')  # Mark cluster centers
plt.title('Vehicle Positions with Lateral Position Clusters')
plt.xlabel('Displacement (x)')
plt.ylabel('Lateral Position (y)')
plt.legend(title='Cluster')
plt.grid(True)
plt.show()centers.flatten()import pandas as pd
from sklearn.cluster import KMeans
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt# 使用肘部法则确定最佳聚类数
sse = {}
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(data[['y']])sse[k] = kmeans.inertia_# 假设根据图形分析选择了最佳的聚类数
optimal_k = 6
kmeans = KMeans(n_clusters=optimal_k, random_state=42)
data['lane'] = kmeans.fit_predict(data[['y']])# 对每个聚类分析x坐标的变化
directions = {}
for lane in range(optimal_k):lane_data = data[data['lane'] == lane]model = LinearRegression()model.fit(lane_data[['time']], lane_data['x'])slope = model.coef_[0]direction = 'Increasing' if slope > 0 else 'Decreasing'directions[lane] = direction# 绘制轨迹plt.scatter(lane_data['time'], lane_data['x'], label=f'Lane {lane} - {direction}')plt.xlabel('Time')
plt.ylabel('X Coordinate')
plt.title('Vehicle Trajectories by Lane')
plt.legend()
plt.show()# 输出结果表格
results = pd.DataFrame.from_dict(directions, orient='index', columns=['Direction'])
print(results)

% 加载数据
data = readtable('A5.csv');% 显示数据的前几行和描述性统计
head(data)
summary(data)% 使用histogram绘制y值的分布，估计车道
figure;
histogram(data.y, 'BinWidth', 0.1, 'Normalization', 'probability');
title('Distribution of Lateral Position (y)');
xlabel('Lateral Position (y)');
ylabel('Frequency');
grid on;% 使用K-means聚类确定车道数量的最佳值（肘部法则）
y_data = data.y;
sse = zeros(10,1);
for k = 1:10
[idx, C, sumd] = kmeans(y_data, k);
sse(k) = sum(sumd);
end% 绘制肘部图形
figure;
plot(1:10, sse, '-o');
title('Elbow Method For Optimal k');
xlabel('Number of clusters (k)');
ylabel('Sum of squared errors (SSE)');
grid on;% 应用K-means聚类，假设最佳k为5
k = 5;
[idx, C] = kmeans(y_data, k);% 假设最佳聚类数为6，再次运行K-means
k = 6;
[idx, C] = kmeans(data.y, k);data.lane = idx;% 对每个车道的x坐标随时间的变化进行线性回归分析
figure;
hold on;
colors = lines(k);
directions = cell(k, 1);
for i = 1:k
laneData = data(data.lane == i, :);
mdl = fitlm(laneData.time, laneData.x);
slope = mdl.Coefficients.Estimate(2);
direction = 'Increasing';
if slope < 0
direction = 'Decreasing';
end
directions{i} = direction;scatter(laneData.time, laneData.x, 36, colors(i,:), 'DisplayName', sprintf('Lane %d - %s', i, direction));
endxlabel('Time');
ylabel('X Coordinate');
title('Vehicle Trajectories by Lane');
legend('show');
grid on;% 输出方向结果
directions_table = table((1:k)', directions, 'VariableNames', {'Lane', 'Direction'});
disp(directions_table);

这篇关于2024年华中杯B题论文发布+数据预处理问题一代码免费分享的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---