（算法版）基于二值图像数字矩阵的距离变换算法

2024-04-18 02:12
文章标签 算法 图像 距离 矩阵 数字 变换 二值

本文主要是介绍（算法版）基于二值图像数字矩阵的距离变换算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Hi，大家好，我是半亩花海。本项目展示了欧氏距离、城市街区距离和棋盘距离变换的实现方法。通过定义一个距离变换类，对输入图像进行距离变换操作，并生成对应的距离矩阵。在示例中，展示了在一个480x480的全黑背景图像上设置三个前景像素点的距离变换结果。

文章目录

      • 一、距离的定义及分类
      • 二、导入必要库
      • 三、距离变换算法
      • 四、定义距离变换类
      • 五、显示原始图像
      • 六、计算并输出距离变换矩阵
      • 七、可视化距离变换结果
      • 八、完整代码

一、距离的定义及分类

距离是描述图像两点像素之间的远近关系的度量，常见的度量距离有欧式距离、城市街区距离、棋盘距离。以下以两坐标点 a = ( i , j ) a = (i, j) a=(i,j) 和 b = ( k , l ) b = (k, l) b=(k,l) 的距离为例，来说明各种距离的定义方式：

（1）欧式距离 D e D_e De​： 欧式距离的定义源于经典的几何学，与我们数学中所学的简单几何的两点之间的距离一致，为两个像素点坐标值的平方根。欧式距离的优点在于其定义非常地直观，是显而易见的，但缺点在于平方根的计算是非常耗时的。

D e ( a , b ) = ( ( i − k ) 2 ) + ( j − l ) 2 D_e(a, b)=\sqrt{\left((i-k)^2\right)+(j-l)^2} De​(a,b)=((i−k)2)+(j−l)2 ​

（2）城市街区距离 D 4 D_4 D4​： 距离描述的是只允许像素坐标系平面中横向和纵向的移动距离，4表示在这种定义下，像素点是 4 邻接的，即每个点只与它的上、下、左、右相邻的 4 个点之间的距离为 1。

D 4 ( a , b ) = ∣ i − k ∣ + ∣ j − l ∣ D_4(a, b)=|i-k|+|j-l| D4​(a,b)=∣i−k∣+∣j−l∣

（3）棋盘距离 D 8 D_8 D8​： 如果允许在图像坐标系中像素点的对角线方向的移动，就可以得到棋盘距离，8 表示在这种定义下，像素点是 8 邻接的，即每个点只与它的上、下、左、右、四个对角线方向相邻的 8 个点之间的距离为 1。

D 8 ( a , b ) = max ⁡ { ∣ i − k ∣ , ∣ j − l ∣ } D_8(a, b)=\max \{|i-k|,|j-l|\} D8​(a,b)=max{∣i−k∣,∣j−l∣}

二、导入必要库

import numpy as np
import matplotlib.pyplot as plt# 设置字体样式以正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

三、距离变换算法

  • 距离变换是图像中像素点与某个区域块的距离。区域块中的像素点值为 0，临近区域块的像素点有较小的值，离它越远值越大。

以二值图像为例，其中区域块内部的像素值为 1，其他像素值为 0。距离变换给出每个像素点到最近的区域块边界的距离，区域块内部的距离变换结果为0。输入图像如图 1 所示， D 4 D_4 D4​ 距离的距离变换结果如图 2 所示。

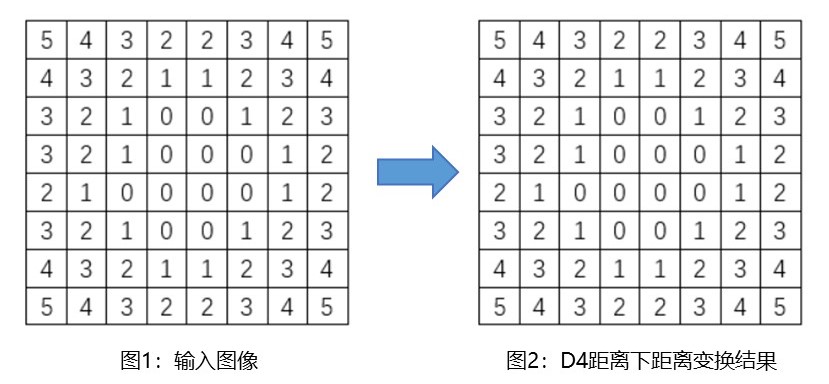
  • 距离变换算法核心是利用两个小的局部掩膜对图像进行遍历。第一遍利用掩模1，左上角开始，从左往右，从上往下；第二遍利用第二个掩模，右下角开始，从右往左，从下往上。掩模形状如下图所示：

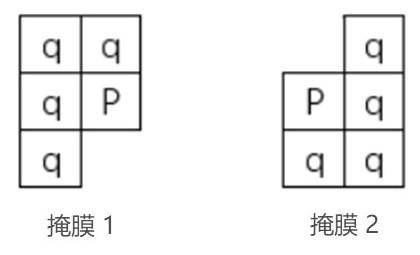
按照某种距离（如： D 4 D_4 D4​ 距离或 D 8 D_8 D8​ 距离）对大小为 M × N M×N M×N 的图像中的区域块作距离变换，算法过程如下：

（1） 建立一个大小为 M × N M×N M×N 的数组 F F F，作如下的初始化：将区域块中的元素设置为 0，其余元素设置为无穷；

（2） 利用掩模1（mask1），左上角开始，从左往右，从上往下遍历数组，将掩模中P点对应的元素的值作如下更新：

F ( P ) = min ⁡ q ∈ mask1 ⁡ { F ( P ) , D ( P , q ) + F ( q ) } F(P)=\min _{q \in \operatorname{mask1}}\{F(P), D(P, q)+F(q)\} F(P)=q∈mask1min​{F(P),D(P,q)+F(q)}

（3） 利用掩模2（mask2），右下角开始，从右往左，从下往上遍历数组，将掩模中P点对应的元素的值作如下更新：

F ( P ) = min ⁡ q ∈ mask2 ⁡ { F ( P ) , D ( P , q ) + F ( q ) } F(P)=\min _{q \in \operatorname{mask2}}\{F(P), D(P, q)+F(q)\} F(P)=q∈mask2min​{F(P),D(P,q)+F(q)}

最终得到的更新后的数组即为距离变换的结果。

因在边界处掩模不能全部覆盖图像，可以将掩模中没有对应元素的位置的值当作 0 来处理，以此对图像边界处做出调整，即maskSize=0。

四、定义距离变换类

在距离变换类当中分别初始化距离变换类、定义欧氏距离和城市街区距离及棋盘距离的函数。

# 定义距离变换类
class DistanceTransform:# 初始化距离变换类def __init__(self, image):self.image = imageself.height, self.width = image.shape# 定义欧氏距离变换def Euclidean_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)# 获取前景像素点的坐标yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的欧氏距离distances = np.sqrt((y - yy) ** 2 + (x - xx) ** 2)# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix# 定义城市街区距离变换def D4_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的曼哈顿距离distances = np.abs(y - yy) + np.abs(x - xx)# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix# 定义棋盘距离变换def D8_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的棋盘距离distances = np.maximum(np.abs(y - yy), np.abs(x - xx))# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix

五、显示原始图像

# 初始化输入图像：480x480的全黑背景
image = np.zeros((480, 480), dtype=np.uint8)
# 取三个前景像素点
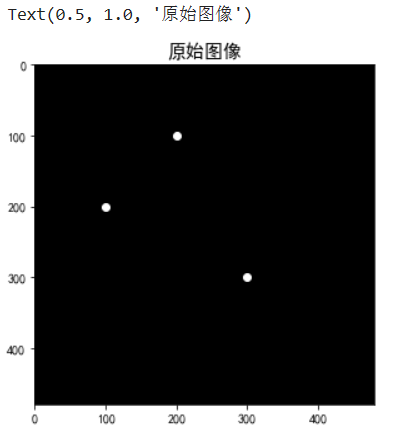
image[100, 200] = 1
image[200, 100] = 1
image[300, 300] = 1# 显示原始图像
plt.figure(figsize=(5, 5))
plt.scatter([100, 200, 300], [200, 100, 300], color='white', marker='o')
plt.imshow(image, cmap='gray')
plt.title('原始图像', fontsize=15)

六、计算并输出距离变换矩阵

# 计算距离变换矩阵
dt = DistanceTransform(image)
euclidean_distance_matrix = dt.Euclidean_distance_transform()
manhattan_distance_matrix = dt.D4_distance_transform()
chessboard_distance_matrix = dt.D8_distance_transform()# 输出欧氏、城区和棋盘的距离矩阵
print("欧氏距离的变换矩阵:\n", euclidean_distance_matrix)
print("城区距离的变换矩阵:\n", manhattan_distance_matrix)
print("棋盘距离的变换矩阵:\n", chessboard_distance_matrix)

七、可视化距离变换结果

# 可视化距离变换结果
plt.figure(figsize=(15, 5))# 欧氏距离变换
plt.subplot(1, 3, 1)
plt.imshow(euclidean_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('欧氏距离', fontsize=15)
plt.axis('off')# 城区距离变换
plt.subplot(1, 3, 2)
plt.imshow(manhattan_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('城区距离', fontsize=15)
plt.axis('off')# 棋盘距离变换
plt.subplot(1, 3, 3)
plt.imshow(chessboard_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('棋盘距离', fontsize=15)
plt.axis('off')plt.tight_layout()
plt.show()

八、完整代码

import numpy as np
import matplotlib.pyplot as plt# 设置字体样式以正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 定义距离变换类
class DistanceTransform:# 初始化距离变换类def __init__(self, image):self.image = imageself.height, self.width = image.shape# 定义欧氏距离变换def Euclidean_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)# 获取前景像素点的坐标yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的欧氏距离distances = np.sqrt((y - yy) ** 2 + (x - xx) ** 2)# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix# 定义城市街区距离变换def D4_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的曼哈顿距离distances = np.abs(y - yy) + np.abs(x - xx)# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix# 定义棋盘距离变换def D8_distance_transform(self):distance_matrix = np.zeros_like(self.image, dtype=float)yy, xx = np.argwhere(self.image == 1).Tfor y in range(self.height):for x in range(self.width):if self.image[y, x] == 1:distance_matrix[y, x] = 0else:# 计算当前像素到前景像素点的棋盘距离distances = np.maximum(np.abs(y - yy), np.abs(x - xx))# 取最小值作为当前像素的距离值distance_matrix[y, x] = np.min(distances)return distance_matrix# 初始化输入图像：480x480的全黑背景
image = np.zeros((480, 480), dtype=np.uint8)
# 取三个前景像素点
image[100, 200] = 1
image[200, 100] = 1
image[300, 300] = 1# 显示原始图像
plt.figure(figsize=(5, 5))
plt.scatter([100, 200, 300], [200, 100, 300], color='white', marker='o')
plt.imshow(image, cmap='gray')
plt.title('原始图像', fontsize=15)# 计算距离变换矩阵
dt = DistanceTransform(image)
euclidean_distance_matrix = dt.Euclidean_distance_transform()
manhattan_distance_matrix = dt.D4_distance_transform()
chessboard_distance_matrix = dt.D8_distance_transform()# 输出欧氏、城区和棋盘的距离矩阵
print("欧氏距离的变换矩阵:\n", euclidean_distance_matrix)
print("城区距离的变换矩阵:\n", manhattan_distance_matrix)
print("棋盘距离的变换矩阵:\n", chessboard_distance_matrix)# 可视化距离变换结果
plt.figure(figsize=(15, 5))# 欧氏距离变换
plt.subplot(1, 3, 1)
plt.imshow(euclidean_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('欧氏距离', fontsize=15)
plt.axis('off')# 城区距离变换
plt.subplot(1, 3, 2)
plt.imshow(manhattan_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('城区距离', fontsize=15)
plt.axis('off')# 棋盘距离变换
plt.subplot(1, 3, 3)
plt.imshow(chessboard_distance_matrix, cmap='gray')
plt.colorbar(shrink=0.8)
plt.title('棋盘距离', fontsize=15)
plt.axis('off')plt.tight_layout()
plt.show()

这篇关于（算法版）基于二值图像数字矩阵的距离变换算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/913500。

相关文章

Python中OpenCV与Matplotlib的图像操作入门指南

Python中OpenCV与Matplotlib的图像操作入门指南

《Python中OpenCV与Matplotlib的图像操作入门指南》：本文主要介绍Python中OpenCV与Matplotlib的图像操作指南,本文通过实例代码给大家介绍的非常详细,对大家的学... 目录一、环境准备二、图像的基本操作1. 图像读取、显示与保存 使用OpenCV操作2. 像素级操作3.
阅读更多...
C/C++中OpenCV 矩阵运算的实现

C/C++中OpenCV 矩阵运算的实现

《C/C++中OpenCV矩阵运算的实现》本文主要介绍了C/C++中OpenCV矩阵运算的实现,包括基本算术运算（标量与矩阵）、矩阵乘法、转置、逆矩阵、行列式、迹、范数等操作,感兴趣的可以了解一下... 目录矩阵的创建与初始化创建矩阵访问矩阵元素基本的算术运算 ➕➖✖️➗矩阵与标量运算矩阵与矩阵运算 (逐元
阅读更多...
C/C++的OpenCV 进行图像梯度提取的几种实现

C/C++的OpenCV 进行图像梯度提取的几种实现

《C/C++的OpenCV进行图像梯度提取的几种实现》本文主要介绍了C/C++的OpenCV进行图像梯度提取的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的... 目录预www.chinasem.cn备知识1. 图像加载与预处理2. Sobel 算子计算 X 和 Y
阅读更多...
c/c++的opencv图像金字塔缩放实现

c/c++的opencv图像金字塔缩放实现

《c/c++的opencv图像金字塔缩放实现》本文主要介绍了c/c++的opencv图像金字塔缩放实现,通过对原始图像进行连续的下采样或上采样操作,生成一系列不同分辨率的图像,具有一定的参考价值,感兴... 目录图像金字塔简介图像下采样 (cv::pyrDown)图像上采样 (cv::pyrUp)C++ O
阅读更多...
Java计算经纬度距离的示例代码

Java计算经纬度距离的示例代码

《Java计算经纬度距离的示例代码》在Java中计算两个经纬度之间的距离,可以使用多种方法（代码示例均返回米为单位）,文中整理了常用的5种方法,感兴趣的小伙伴可以了解一下... 目录1. Haversine公式（中等精度，推荐通用场景）2. 球面余弦定理（简单但精度较低）3. Vincenty公式（高精度，
阅读更多...
使用雪花算法产生id导致前端精度缺失问题解决方案

使用雪花算法产生id导致前端精度缺失问题解决方案

《使用雪花算法产生id导致前端精度缺失问题解决方案》雪花算法由Twitter提出,设计目的是生成唯一的、递增的ID,下面：本文主要介绍使用雪花算法产生id导致前端精度缺失问题的解决方案,文中通过代... 目录一、问题根源二、解决方案1. 全局配置Jackson序列化规则2. 实体类必须使用Long封装类3.
阅读更多...
Python+wxPython构建图像编辑器

Python+wxPython构建图像编辑器

《Python+wxPython构建图像编辑器》图像编辑应用是学习GUI编程和图像处理的绝佳项目,本教程中,我们将使用wxPython,一个跨平台的PythonGUI工具包,构建一个简单的... 目录引言环境设置创建主窗口加载和显示图像实现绘制工具矩形绘制箭头绘制文字绘制临时绘制处理缩放和旋转缩放旋转保存编
阅读更多...
Springboot实现推荐系统的协同过滤算法

Springboot实现推荐系统的协同过滤算法

《Springboot实现推荐系统的协同过滤算法》协同过滤算法是一种在推荐系统中广泛使用的算法,用于预测用户对物品（如商品、电影、音乐等）的偏好,从而实现个性化推荐,下面给大家介绍Springboot... 目录前言基本原理 算法分类 计算方法应用场景 代码实现 前言协同过滤算法（Collaborativ
阅读更多...
python+OpenCV反投影图像的实现示例详解

python+OpenCV反投影图像的实现示例详解

《python+OpenCV反投影图像的实现示例详解》：本文主要介绍python+OpenCV反投影图像的实现示例详解,本文通过实例代码图文并茂的形式给大家介绍的非常详细,感兴趣的朋友一起看看吧... 目录一、前言二、什么是反投影图像三、反投影图像的概念四、反向投影的工作原理一、利用反向投影backproj
阅读更多...
使用Python实现图像LBP特征提取的操作方法

使用Python实现图像LBP特征提取的操作方法

《使用Python实现图像LBP特征提取的操作方法》LBP特征叫做局部二值模式,常用于纹理特征提取,并在纹理分类中具有较强的区分能力,本文给大家介绍了如何使用Python实现图像LBP特征提取的操作方... 目录一、LBP特征介绍二、LBP特征描述三、一些改进版本的LBP1.圆形LBP算子2.旋转不变的LB
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2