椭圆曲线密码学（ECC）基本介绍和总结

本文主要是介绍椭圆曲线密码学（ECC）基本介绍和总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

背景

ECC英文全称"Elliptic Curve Cryptography"，其背后的密码学原理或者说安全性，是基于椭圆曲线离散对数问题（Elliptic Curve Discrete Logarithm Problem，ECDLP）。ECC密码学被普遍认为是RSA密码系统的接替算法，相比于RSA，ECC在使用更短的密钥长度即可达到同等的安全性，比如ECC164位的密钥，相当于RSA 1024位密钥提供的保密强度，且由于密钥更短，运算速度和带宽占用上也更有优势。
关于ECC的数学原理介绍和使用方法，网上有许多教程，下面主要是个人对认为比较难理解的知识点的思考和汇总。

椭圆曲线的确定

描述一条Fp上的椭圆曲线，常用到六个参数：
T=(p,a,b,G,n,h)。
p 、a 、b 用来确定一条椭圆曲线，
G为基点，
n为点G的阶，
h 是椭圆曲线上所有点的个数m与n相除的整数部分。
这几个参数取值的选择，直接影响了加密的安全性。参数值一般要求满足以下几个条件：

1. p 当然越大越安全，但越大，计算速度会变慢，200位左右可以满足一般安全要求；
2. p≠n×h；
3. pt≠1 (mod n)，1≤t<20；
4. 4a3 + 27b2 ≠ 0 (mod p)；
5. n 为素数；
6. h≤4

椭圆曲线的选择

使用ECC时，应该从密码学家证明过具备安全性的曲线中选择曲线使用，如secp256k1, P-521 ，Curve25519等，不应该使用私有的曲线。即不要自行选择或者定义T=(p,a,b,G,n,h)中这些确定椭圆曲线的参数。

密钥长度的选项和选择

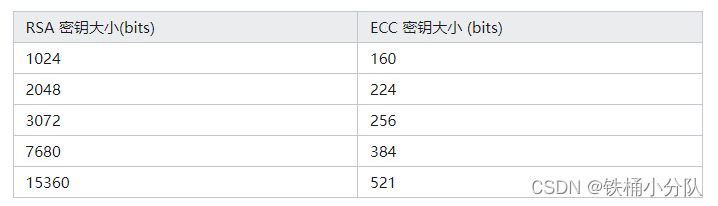
由于我们对RSA比较熟悉，因此我们可以把两种算法中不同密钥长度的安全性进行类比，这样就可以基于RSA的经验，来选择合适的密钥长度，下表是两种算法，在提供同等级安全时，各自需要的密钥长度。就RSA而言，目前主流密钥长度至少都是1024bits以上，低于或者等于1024bit的密钥已经不建议使用，对于一些政府部门，金融机构，应选择使用大于2048bits的密钥长度。

椭圆曲线明文，密文，密钥和椭圆曲线的关系

很多文章对椭圆曲线的数学原理的解释十分详细，但是看完还是没办法理解是如何将这个曲线和加解密联系在一起。其实明文，密文以及公钥都是椭圆曲线上的点或者点对。
私钥：生成一个随机数k_priv，这个随机数的范围是[1,n)，即大于0，但是小于n的数，n即曲线的阶，是椭圆曲线的参数之一，在曲线确定的情况下，这个n值也可以确定
公钥：k_pub = k_privG，其中G是T=(p,a,b,G,n,h)中的G，即椭圆曲线的生成元（或者叫基点），通过k_priv和G相乘得到的k_pub 仍然是在曲线上的一点
明文：将明文编码，使之成为T=(p,a,b,G,n,h)曲线上的一点，表示为M
密文：生成随机数r，将消息M生成密文E，E = {rG, M+rk_pub }，其中k_pub 为公钥，这个密文就是曲线上的一个点对
解密过程：
密文 = E = M + rk_pub - k_priv*(rG) = M + r(k_privG) - k_priv (rG) = M
在数学上，已知k_priv和G，求k_pub = k_privG的速度是非常快的，但是已知k_pub 和G，求k_priv=k_pub/G却是非常困难的，这就是椭圆曲线的离散对数问题，ECC加解密算法的安全性正是基于这个离散对数问题而得到保证
综上，可以简述加解密过程如下：

1. 用户A选定一条椭圆曲线T=(p,a,b,G,n,h)
2. 用户A选择一个私有密钥k，并生成公开密钥K=kG
3. 用户A将曲线T（实际中，则是双方约定选择同一个经过安全证明的曲线）和点K（公钥），G传给用户B
4. 用户B接到信息后，将待传输的明文编码到曲线T上一点M，并产生一个随机整数r（r<n）
5. 用户B计算点C1=M+rK；C2=rG
6. 用户B将C1、C2传给用户A
7. 用户A接到信息后，计算C1-kC2，结果就是点M。因为C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M
8. 再对点M进行解码就可以得到明文。
   在这个加密通信中，如果有一个偷窥者H ，他只能看到T=(p,a,b,G,n,h)、K、G、C1、C2，而通过K、G 求k 或通过C2、G求r 都是相对困难的。因此，H无法得到A、B间传送的明文信息。

公钥和私钥的表示方式

公钥

椭圆曲线的公钥实际上是曲线上的一个点，可以用坐标点（x,y）表示，通常是将x和y的值分别转换成字符串来存储和传输，如下是一个公钥的例子
57E1174B773A91E743BC719C9C8B24C8F25096411744C0EB09C13AAD4073D547
BBD7DA078002F7C84441B196A8B8532E0046BA8ED71DED0B9E2BEACA31F1EE9A
其中57E1174B773A91E743BC719C9C8B24C8F25096411744C0EB09C13AAD4073D547为公钥的x点坐标，BBD7DA078002F7C84441B196A8B8532E0046BA8ED71DED0B9E2BEACA31F1EE9A为公钥的y点坐标，实际在计算的时候，需要把这些字符串中的元素按照其字面的值转为对应的十六进制，如：0x57，0xE1…
上述是公钥的非压缩表示，通常需要还在坐标点前加上一个字节0x04用于表示使用非压缩的方式，即0457E1174B773A91E743BC719C9C8B24C8F25096411744C0EB09C13AAD4073D547BBD7DA078002F7C84441B196A8B8532E0046BA8ED71DED0B9E2BEACA31F1EE9A。
还有一种压缩的表示方式。根据椭圆曲线方程，我们只需要知道 x 坐标，就可以通过方程计算出 y 坐标，这样就不用同时保存x，y的值，减少了存储和带宽。但是如果只知道x，带入方程会求出两个y，一正一负，对应两个不同的点，所以还必须有一个标志来区别实际使用的是哪个。所以通常采用下面的约定，具体格式为：

• 前缀02 + x （当y为偶数）
• 前缀03 + x （当y为奇数）
  可以仅用一个坐标长度+1bit表示整个公钥，比如：
  02f54ba86dc1ccb5bed0224d23f01ed87e4a443c47fc690d7797a13d41d2340e1a

私钥

私钥是一个随机数，通常是把其十六进制下的数据当作字符串保存（和公钥的保存形式一样），如下：
0A7ECE7EFCA5C5A186FF7340125E2E1F1754D8F27922573F66ABA43D8DA3ECDE
这个私钥其实就是0x0A，0x7E，0xCE…

椭圆曲线加解密算法的实现

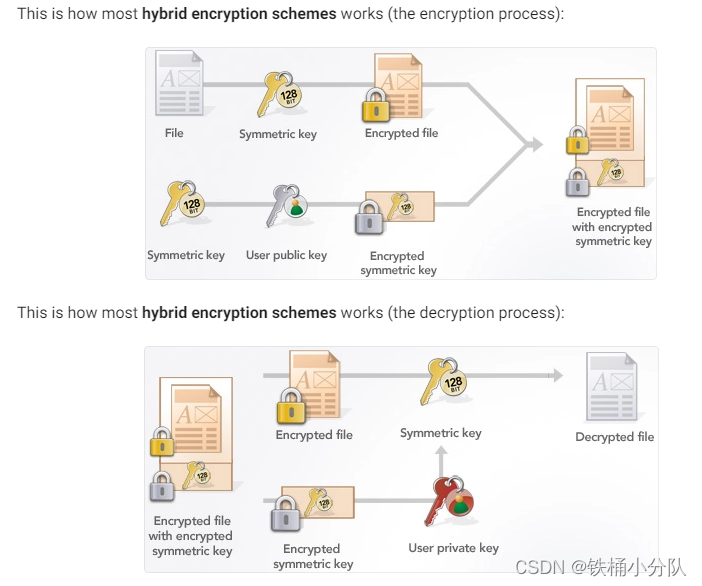
但是实际上，和RSA算法不同，ECC并没有提供/定义一种具体的加解密算法，在目前常用的开源算法库中，也没有看到直接实现ECC加解密的接口，为了基于ECC实现加解密，开发人员通常采用混合加密方案来实现此功能，下面是混合加密解决方案的示例图，其实就是结合对称加解密，密钥派生算法，或者密钥协商算法等其他密码学算法，同时结合ECC的安全性，间接实现ECC加解密。

下面是一个基于ECDH密钥交换方案设计的ECC加解密功能实例
由于使用的密钥较多，先逐一介绍这些密钥的功能以及如何产生这些密钥
sharedSecret：共享秘密数，通过密钥协商算法生成的临时秘密数，用于作为密钥派生算法（KDF）的输入，派生出加密明文的加密密钥和摘要计算密钥
sendTempPub：发送方的临时ECC公钥，用于计算sharedSecret
sendTempPriv：发送方的临时ECC私钥，用于计算sharedSecret
recvPubKey：接收方的固定的ECC公钥，同时也是对外暴露的公钥，需要给到发送方
recvPrivKey：接收方的固定的ECC私钥
ENC Key：用于对实际明文进行加解密的对称密钥
MAC Key：用于进行hash计算的对称密钥
关于密钥协商的过程，通常使用DH算法，可以参考下面的介绍：
https://cryptobook.nakov.com/asymmetric-key-ciphers/ecdh-key-exchange

加密过程

假设用户A需要通过ECIES对数据进行加密，发送给用户B
加密步骤如下：

1. 用户B生成随机数（并不是任意的随机数都可以，需要是[1,n)这个范围内，n为阶数，曲线的参数之一），作为recvPrivKey
2. 用户B通过私钥recvPrivKey，生成公钥recvPubKey：recvPrivKey*G=recvPubKey（G为生成元，也是曲线的参数之一），并将公钥recvPubKey给到用户A
3. 用户A生成随机数，作为sendTempPriv，并计算出sendTempPub=sendTempPriv*G
4. 用户A通过：sendTempPriv*recvPubKey = SharedSecret，得到SharedSecret
5. 用户A将SharedSecret作为输入，通过KDF算出ENC Key和MAC Key
6. 使用ENC Key对明文m进行加密，得到c
7. 使用MAC Key对上一步得到的c进行MAC计算，得到tag
8. 将sendTempPub，c和tag拼接，得到sendTempPub | c | tag，作为完整的密文发送给到B
   上述过程的图形表示如下：
   

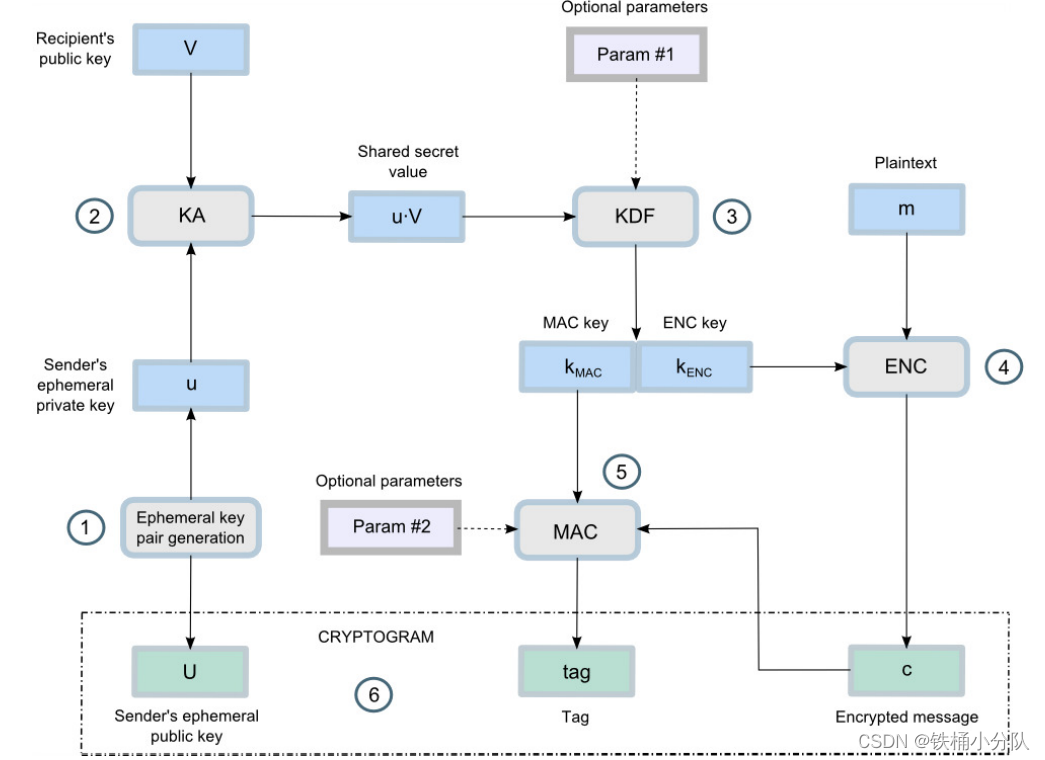
解密过程

假设用户B收到了来自用户A的密文：sendTempPub | c | tag
解密步骤如下：

1. 用户B从sendTempPub | c | tag提取出sendTempPub
2. 用户B使用sendTempPub * recvPrivKey计算出SharedSecret，用户A是通过sendTempPriv * recvPubKey = SharedSecret计算出SharedSecret的，又因为sendTempPub = sendTempPriv * G，因此sendTempPub * recvPrivKey = sendTempPriv * G * recvPrivKey = sendTempPriv * recvPubKey = SharedSecret
3. 用户B以SharedSecret作为输入，通过KDF算出ENC Key和MAC Key
4. 用户B从sendTempPub | c | tag提取出c
5. 用户B使用ENC Key对c进行解密，得到明文m
6. 用户B从sendTempPub | c | tag提取出tag
7. 用户B使用MAC Key对c进行hash计算，得到tag’
8. 将tag和tag’进行比较
   上述过程的图形表示如下：
   
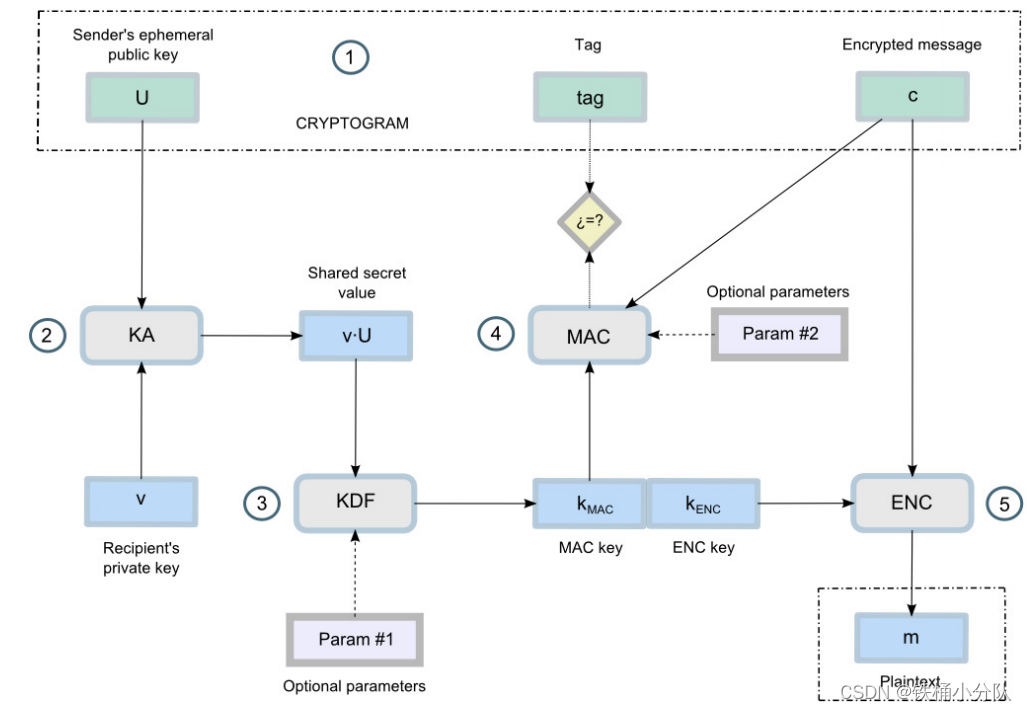
   综上，可以看到ECC在加解密中，主要是利用私钥的不可逆推来保护临时的对称密钥的安全性，真正加密数据的是通过密钥派生算法计算出的密钥。
   从上述的例子可以看出，基于ECC进行加解密的方案中，具体使用何种密钥派生算法，何种对称加解密算法，都是非常灵活的，为了便于加解密双方协商这些算法或者参数，实际工程中，可以基于ECIES来实现加解密方案。ECIES（集成加密方案，elliptic curve integrate encrypt scheme），ECIES并不是一种具体的方案，而是一种基于ECC的加解密框架，其中的密钥导出机制，加密方法都可以根据自己的需要进行设计。
   ECIES也有几个标准：ANSI X9.63， IEEE 1363a 和 ISO/IEC 18033-2。其中主要约定ECIES参数是KDF，对称加解密算法，MAC算法等。

ECC和RSA的比较

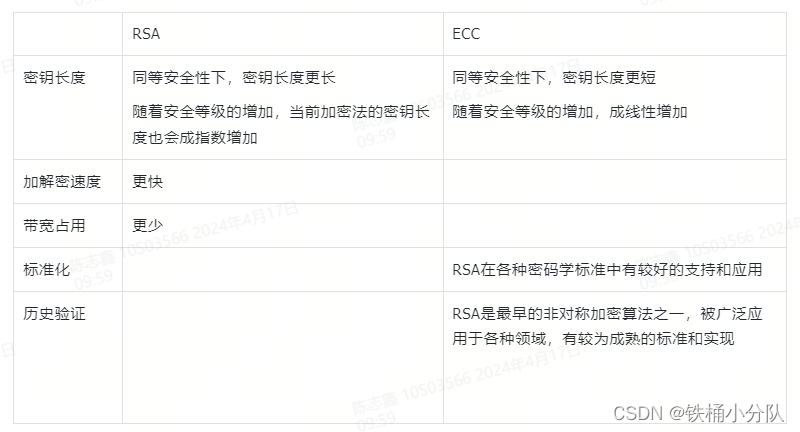
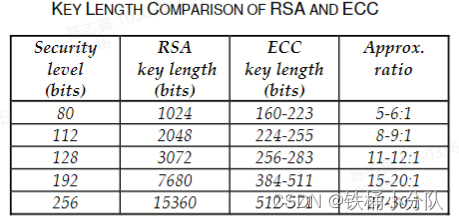
这篇关于椭圆曲线密码学（ECC）基本介绍和总结的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---