本文主要是介绍二路归并排序的算法设计和复杂度分析(C语言),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
实验内容:
实验过程:
1.算法设计
2.程序清单
3.运行结果
4.算法复杂度分析
实验内容:
二路归并排序的算法设计和复杂度分析。
实验过程:
1.算法设计
二路归并排序算法,分为两个阶段,首先对待排序列进行拆分,然后进行合并排序。
第一阶段:将待排序列分长度成大致相等的两个子序列,按照同样的拆分方法,对每个子序列进行拆分,直到子序列中只有一个元素。
第二阶段:对拆分的结果,自底向上将相邻的两个有序序列合并排序。
2.程序清单
#include<stdio.h>
#include<malloc.h>
void disp(int a[],int n)
{int i;for(i=0;i<n;i++)printf("%d ",a[i]);printf("\n");
}
//将两个相邻的有序子序列归并为一个有序子序列
void Merge(int a[],int low,int mid,int high)
{int *tmpa;//创建临时数组tmpa储存合并结果int i=low,j=mid+1,k=0;//k是tmpa的下标,i,j分别为两个子表的下标tmpa=(int *)malloc((high-low+1)*sizeof(int));while(i<=mid&&j<=high)if(a[i]<=a[j])//将第一个子表中的元素放入tmpa中{tmpa[k]=a[i];i++;k++;}else//将第二个子表中的元素放入tmpa中{tmpa[k]=a[j];j++;k++;}while(i<=mid)//将第一个子表余下的部分复制到tmpa中{tmpa[k]=a[i];i++;k++;}while(j<=high)//将第二个子表余下的部分复制到tmpa中国{tmpa[k]=a[j];j++;k++;}for(k=0,i=low;i<=high;k++,i++)//将tmpa复制到a中a[i]=tmpa[k];free(tmpa);
}//二路归并算法
void MergeSort(int a[],int low,int high)
{int mid;if(low<high){mid=(low+high)/2;MergeSort(a,low,mid);//对a[low,mid]子序列排序MergeSort(a,mid+1,high);//对a[mid+1,high]子序列排序Merge(a,low,mid,high);//将两个子序列合并}
}
void main()
{int n=10;int a[]={1,5,2,4,10,6,3,8,9,10};printf("排序前");disp(a,n);MergeSort(a,0,n-1);printf("排序后");disp(a,n);
}3.运行结果
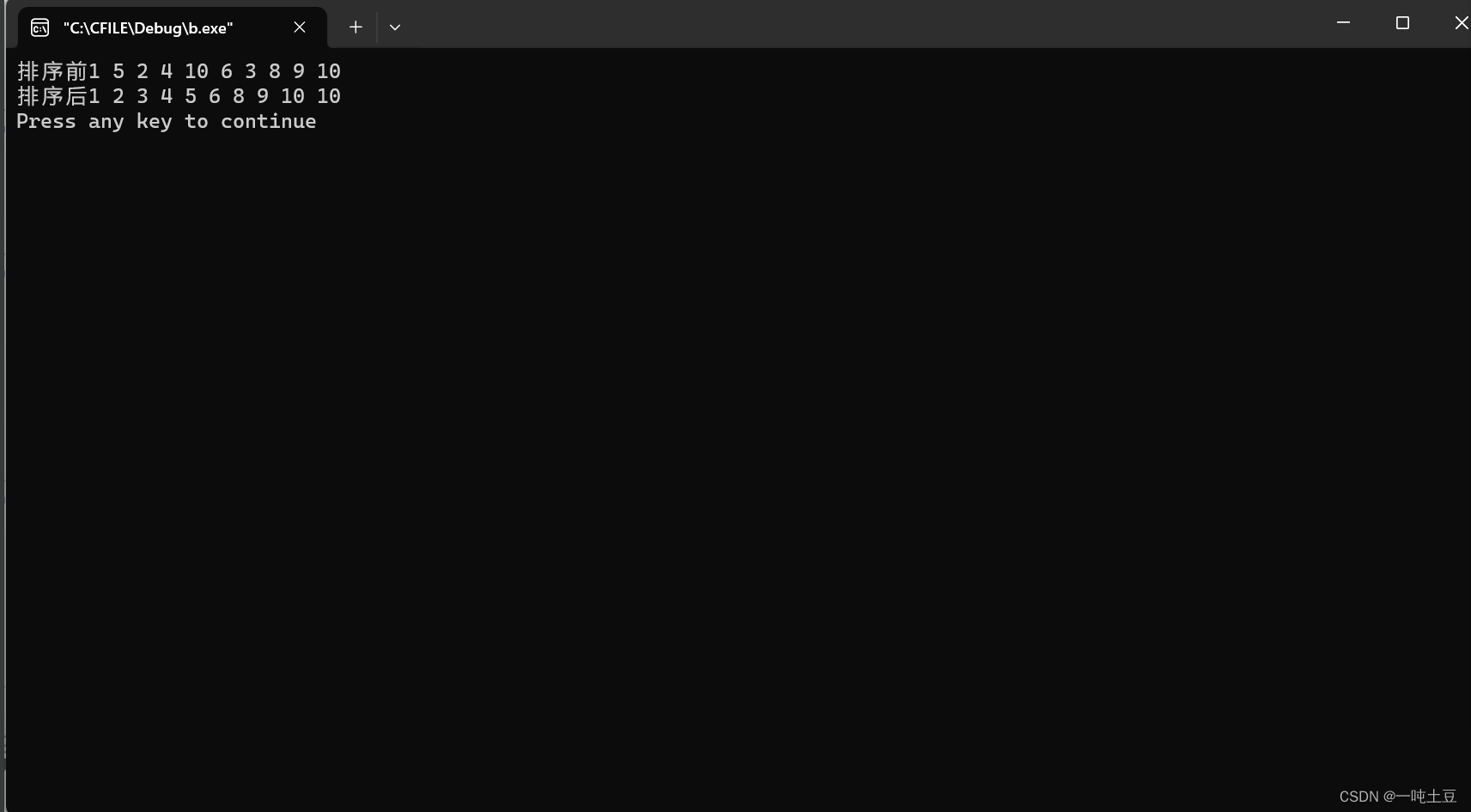
4.算法复杂度分析
设MergeSort(a,0,n-1)算法的执行时间为T(n),显然Merge(a,0,n/2,n-1)合并操作的执行时间为O(n),所有得到以下递推式:
当n=1时,T(n)=1
当n>1时,T(n)=2T(n/2)+O(n)
故二路归并排序的算法时间复杂度为O(nlogn)
在算法中需要一个一维数组辅存储排序结果,所以空间复杂度为O(n)
这篇关于二路归并排序的算法设计和复杂度分析(C语言)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





