本文主要是介绍day58 回文子串 最长回文子序列,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目1:647 回文子串
题目链接:647 回文子串
题意
统计字符串s中回文子串的数目
回文子串是正着读和倒过来读一样的字符串 子串是连续字符组成的一个序列
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i][j] 表示 [s[i],s[j]]范围内的子串是否是回文串 若是则dp[i][j] = true
2)dp数组初始化
根据dp数组定义 dp[i][j] = false;
3)递推公式
if(s[i] != s[j]) 肯定不是回文子串,对最终的结果没有什么影响,所以不做考虑
if(s[i] == s[j]) 这个是大前提 考虑出现回文子串的情况:
情况1 i == j 指向了同一个元素 此时只有1个元素作为子串 是回文子串 dp[i][j] = true;
情况2 j - i == 1 相邻元素相同,是一个回文子串 dp[i][j] = true;
情况3 j - i > 1 取决于[s[i+1],s[j-1]]是否是回文子串 if(dp[i+1][j-1] == true) dp[i][j]=true;

4)遍历顺序
根据递推公式,从下往上遍历 从左往右遍历
for(int i = s.size()-1; i >= 0; i--){
for(int j = i; j < s.size(); j++){
}
}

5)打印dp数组
代码
class Solution {
public:int countSubstrings(string s) {//定义dp数组 初始化dp数组vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for(int i = s.size() - 1; i >= 0; i--){for(int j = i; j < s.size(); j++){if(s[i] == s[j]){if(i == j){dp[i][j] = true;result++;} else if(j - i == 1){dp[i][j] = true;result++;}else if(j - i > 1){if(dp[i+1][j-1] == true){dp[i][j] = true;result++;}}}//cout<< "i=" << i << " " << "j=" << j << " " << dp[i][j] << " " << "result=" <<result << endl;}}return result;}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
题目2:516 最长回文子序列
题目链接:516 最长回文子序列
题意
找出回文子序列的最长长度
子序列可以在不改变元素顺序的情况下,删除/不删除某个字符形成的
和647 最长回文子串的区别是,这个可以选择删除中间元素,只要不改变原顺序
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i][j] 在[s[i],s[j]] 内最长回文子串的长度
2)dp数组初始化
i==j 时,指向同一个元素 dp[i][i] = 1
其他下标对应的dp[i][j]初始化为0
3)递推公式
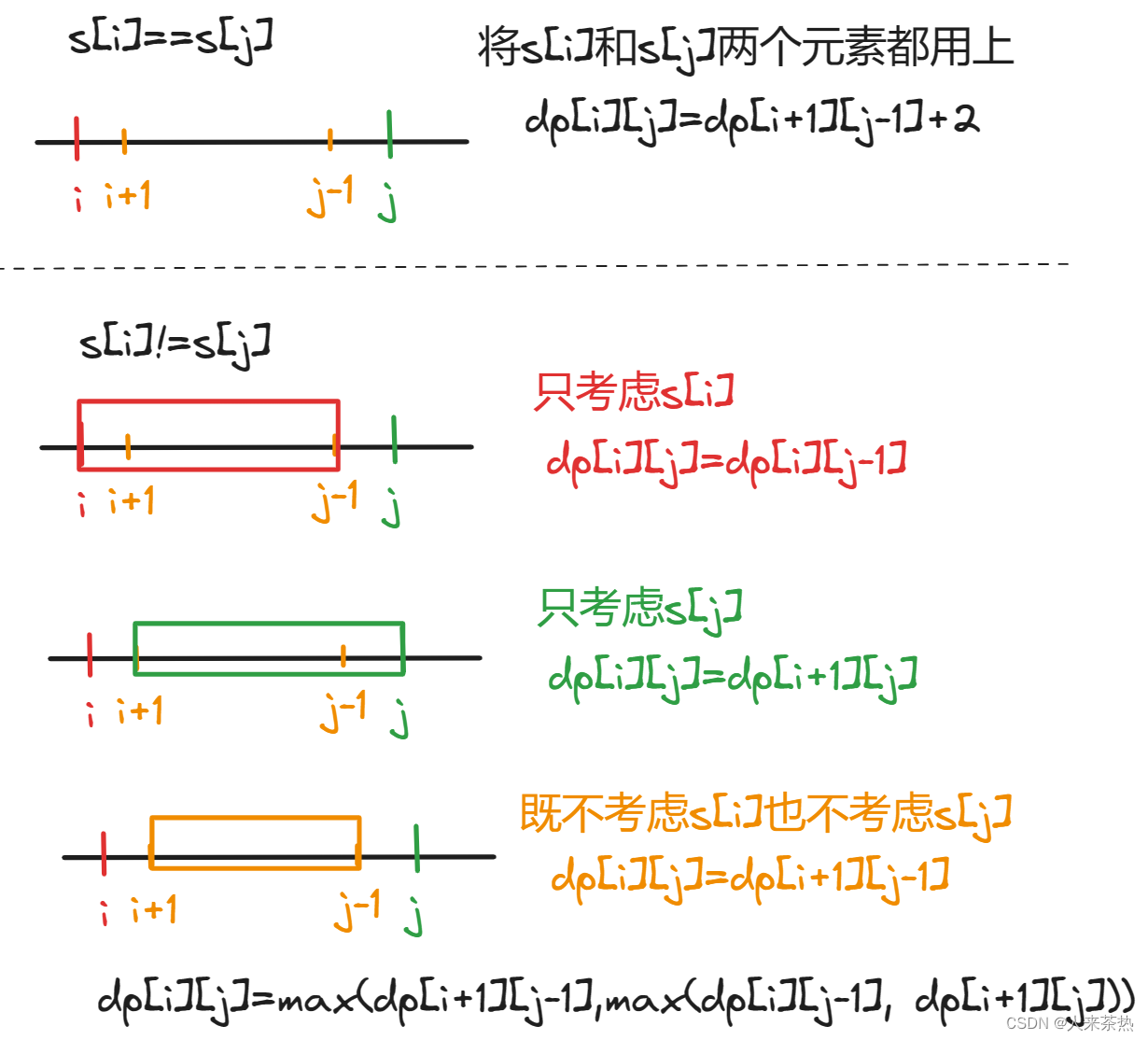
if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2
else dp[i][j] = max(dp[i+1][j],dp[i][j-1])
4)遍历顺序
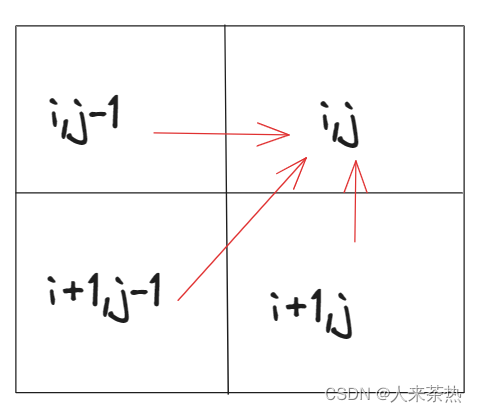
根据递推公式 从下往上遍历 从左往右遍历
for(int i = s.size(); i >= 0; i--){
for(int j = i+1; j <s.size(); j++){
}
} 两个for循环不能颠倒顺序,因为j的状态依赖于i的状态
5)打印dp数组
代码
class Solution {
public:int longestPalindromeSubseq(string s) {//定义dp数组 初始化vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for(int i = 0; i < s.size(); i++) dp[i][i] = 1;for(int i = s.size() - 1; i >= 0; i--){for(int j = i + 1; j < s.size(); j++){if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2;else {dp[i][j] = max(dp[i+1][j-1], max(dp[i][j-1], dp[i+1][j]));}}}return dp[0][s.size() - 1];}
};- 时间复杂度: O(n^2)
- 空间复杂度: O(n^2)
这篇关于day58 回文子串 最长回文子序列的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






