本文主要是介绍JavaScript排序大揭秘:手绘图解6大常见排序算法,一网打尽,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
📫 大家好,我是南木元元,热爱技术和分享,欢迎大家交流,一起学习进步!
🍅 个人主页:南木元元
本文用图解总结梳理了6种常见的排序算法 ,如下👇:
- 冒泡排序
- 选择排序
- 插入排序
- 快速排序
- 归并排序
- 堆排序
目录
一.冒泡排序
思路及图解
代码实现
二.选择排序
思路及图解
代码实现
三.插入排序
思路及图解
代码实现
四.快速排序
思路及图解
代码实现
五.归并排序
思路及图解
代码实现
六.堆排序
思路及图解
代码实现
结语
一.冒泡排序
思路及图解
- 基本思路
冒泡排序的基本思路:比较相邻的两个元素,将较大的元素交换到后面。通过多次遍历和两两比较,使得每一轮遍历都能确定一个当前未排序元素的最终位置,直至所有元素有序。
- 冒泡排序图解

时间复杂度:O(n^2);空间复杂度:O(1)
代码实现
下面是用 JavaScript 实现的冒泡排序代码:
function bubbleSort(arr) {//外循环控制比较次数:n-1次for (let i = 0; i < arr.length - 1; i++) {// 内循环控制比较元素for (let j = 0; j < arr.length - 1 - i; j++) {// 如果前一个元素比后一个元素大,则交换它们的位置if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; }}}return arr;
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bubbleSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]- 优化版
如果在某一轮比较中没有发生元素交换,则说明数组已经有序,可以提前结束排序过程。
function bubbleSort(arr) {let flag; // 标记位for (let i = 0; i < arr.length; i++) {flag = false;for (let j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {flag = true; // 发生了交换[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];}}if (!flag) break; // 如果一轮比较后没有发生交换,说明已经有序}return arr;
}二.选择排序
思路及图解
- 基本思路
选择排序的基本思路:每次从未排序的部分中选择最小(或最大)的元素,然后将其与未排序部分的第一个元素交换位置,直到整个数组排序完成。
- 选择排序图解

时间复杂度:O(n^2);空间复杂度:O(1)
代码实现
下面是用 JavaScript 实现的选择排序代码:
function selectSort(arr) {for (let i = 0; i < arr.length - 1; i++) {let minIndex = i; // 假设当前位置是最小值的位置// 在未排序部分找到最小元素的索引 for (let j = i + 1; j < arr.length; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 如果当前循环的索引不是最小数的索引,交换它们if(i !== minIndex) {[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];}}return arr;
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(selectSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]三.插入排序
思路及图解
- 基本思路
基本思想:将待排序的数组分成已排序区间和未排序区间,初始时已排序区间只有一个元素,然后逐步将未排序区间的元素插入到已排序区间的合适位置,直到整个数组排序完成。
整个过程就像打扑克牌,从牌堆顶取一张牌,找到合适的位置插入到已有牌的顺序中。

- 插入排序图解

时间复杂度:O(n^2);空间复杂度:O(1)
代码实现
下面是用 JavaScript 实现的插入排序代码:
function insertionSort(arr) {for (let i = 1; i < arr.length; i++) {// 当前待插入的元素let current = arr[i]; let j = i - 1;// 将大于当前元素的元素都向后移动while (j >= 0 && arr[j] > current) {arr[j + 1] = arr[j];j--;}// 找到合适的位置插入当前元素arr[j + 1] = current; }return arr;
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(insertionSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]四.快速排序
思路及图解
- 基本思路
快排采用分治的思想,选择一个基准元素,将数组分割成两个子数组,小于基准元素的放在左边,大于基准元素的放在右边,然后对这两个子数组进行递归排序,直到左右两部分只剩下一个数。
- 快速排序图解

时间复杂度:O(nlogn);空间复杂度:O(logn)
代码实现
下面是用 JavaScript 实现的快速排序代码:
function quickSort(arr) {//递归出口,如果数组长度小于等于1,直接返回数组,无需排序if (arr.length <= 1) {return arr; }// 选取数组的第一个元素作为基准元素const pivot = arr[0]; // 用于存放小于等于基准元素的部分const left = []; // 用于存放大于基准元素的部分const right = []; // 将小于等于基准元素的数放入 left 数组,大于基准元素的放入 right 数组for (let i = 1; i < arr.length; i++) {if (arr[i] <= pivot) {left.push(arr[i]); } else {right.push(arr[i]); }}// 递归地对左右两个部分进行排序return [...quickSort(left), pivot, ...quickSort(right)];
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(quickSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]五.归并排序
思路及图解
- 基本思路
归并排序是一种经典的分治算法,核心思想是将待排序数组分成若干个子序列,分别进行排序,然后将已排序的子序列合并成更大的有序序列,直到整个数组排序完成。
- 归并排序图解

时间复杂度:O(nlogn);空间复杂度:O(n)
代码实现
下面是用 JavaScript 实现的归并排序代码:
function mergeSort(arr) {// 如果数组长度小于 2,不需要排序,直接返回if (arr.length < 2) {return arr;}let mid = Math.floor(len / 2);// 将数组从中间位置分为左右两个子数组let l = arr.slice(0, mid);let r = arr.slice(mid);// 递归调用mergeSort对左右两个子数组进行排序,并将结果合并return merge(mergeSort(l), mergeSort(r));
}function merge(left, right) {let arr = [];// 排序并合并两个数组while (left.length && right.length) {if (left[0] <= right[0]) {arr.push(left.shift());} else {arr.push(right.shift());}}// 合并左右子数组中剩余的元素return arr.concat(left, right);
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(mergeSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]六.堆排序
思路及图解
- 基本思路
堆排序的基本思路:先将待排序的数组构建成一个最大堆(或最小堆),然后依次将堆顶元素与堆尾元素交换并重新调整堆,重复这个过程直到整个数组排序完成。
1.构建最大堆。将待排序的数组视为完全二叉树,从最后一个非叶子节点开始,依次向前调整节点,使得每个节点都满足父节点的值大于或等于子节点的值。
2.交换并调整堆。将堆顶元素(即当前最大的元素)与堆尾元素交换,然后重新调整剩余的元素,使得剩余元素重新构成一个最大堆。重复这个过程,直到所有元素都被排序完成。
- 堆排序图解
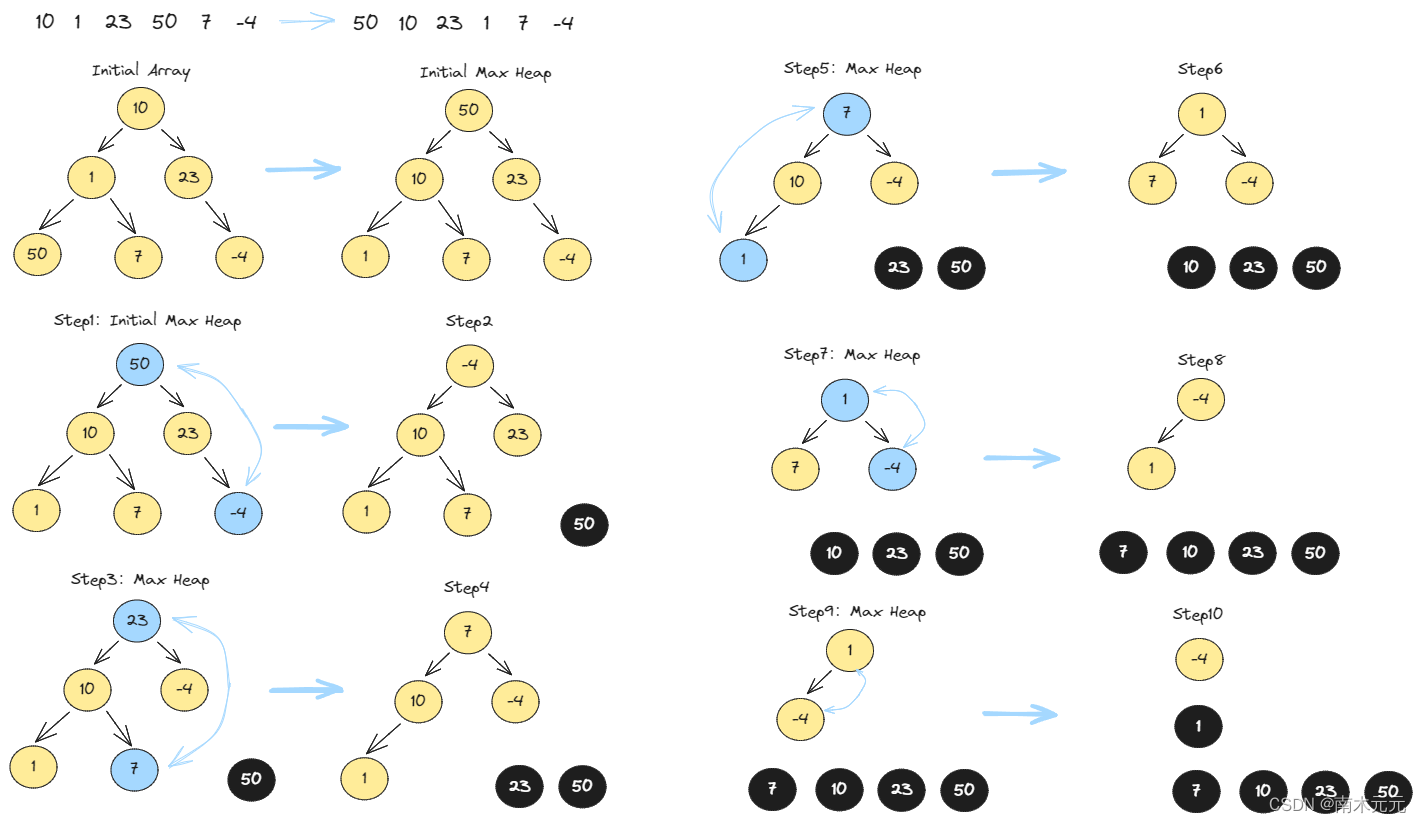
时间复杂度:O(nlogn);空间复杂度:O(1)
代码实现
下面是用 JavaScript 实现的堆排序代码:
// 调整堆,使得剩余元素重新构成最大堆
function heapify(arr, n, i) {let l = i * 2 + 1;let r = i * 2 + 2;let max = i;// 找出左右子节点和当前节点中的最大值if (l < n && arr[l] > arr[max]) {max = l;}if (r < n && arr[r] > arr[max]) {max = r;}// 如果最大值不是当前节点,交换节点并继续调整堆if (max !== i) {[arr[max], arr[i]] = [arr[i], arr[max]];heapify(arr, n, max);}
}
// 堆排序
function heapSort(arr) {let len = arr.length;// 建立大根堆,从最后一个非叶子节点开始let last = Math.floor((len - 2) / 2);for (let i = last; i >= 0; i--) {heapify(arr, len, i);}// 每次把堆顶的数与最后一个数交换,并重新调整堆for (let i = 0; i < len; i++) {[arr[0], arr[len - 1 - i]] = [arr[len - 1 - i], arr[0]];heapify(arr, len - 1 - i, 0);}return arr;
}// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(heapSort(arr));
// 输出:[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]结语
🔥如果此文对你有帮助的话,欢迎💗关注、👍点赞、⭐收藏、✍️评论,支持一下博主~
这篇关于JavaScript排序大揭秘:手绘图解6大常见排序算法,一网打尽的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








