本文主要是介绍[2019红帽杯]childRE 分析与拓展,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
十分特殊也有趣的一题,特此记录。流程并非难以理解,但有些需要注意的点。
无壳,可以直接用IDA分析,但由于存在一些动态变量,一旦开始动调,代码将会变得更难理解,因此目前只用静态调试来审计
int __cdecl main(int argc, const char **argv, const char **envp)
{__int64 v3; // rax__int64 v4; // raxconst CHAR *v5; // r11__int64 v6; // r10int v7; // er9const CHAR *v8; // r10__int64 v9; // rcx__int64 v10; // raxint result; // eaxunsigned int v12; // ecx__int64 v13; // r9__int128 v14[2]; // [rsp+20h] [rbp-38h] BYREFv14[0] = 0i64;v14[1] = 0i64;sub_140001080("%s");v3 = -1i64;do++v3;while ( *((_BYTE *)v14 + v3) );if ( v3 != 31 ){while ( 1 )Sleep(0x3E8u);}v4 = sub_140001280(v14);v5 = name;if ( v4 ){sub_1400015C0(*(_QWORD *)(v4 + 8));sub_1400015C0(*(_QWORD *)(v6 + 16));v7 = dword_1400057E0;v5[dword_1400057E0] = *v8;dword_1400057E0 = v7 + 1;}UnDecorateSymbolName(v5, outputString, 0x100u, 0);v9 = -1i64;do++v9;while ( outputString[v9] );if ( v9 == 62 ){v12 = 0;v13 = 0i64;do{if ( a1234567890Qwer[outputString[v13] % 23] != *(_BYTE *)(v13 + 0x140003478i64) )_exit(v12);if ( a1234567890Qwer[outputString[v13] / 23] != *(_BYTE *)(v13 + 0x140003438i64) )_exit(v12 * v12);++v12;++v13;}while ( v12 < 0x3E );sub_140001020("flag{MD5(your input)}\n");result = 0;}else{v10 = sub_1400018A0(std::cout);std::ostream::operator<<(v10, sub_140001A60);result = -1;}return result;
}第57行是明显的显示验证结果,则能够判明第56行的while为判断条件的遍历;IDA将 ‘!=’ 后面的内容分析成地址而不是数组,但不妨碍提取数据
char fp[] = {"1234567890-=!@#$%^&*()_+qwertyuiop[]QWERTYUIOP{}asdfghjkl;'ASDFGHJKL:\"ZXCVBNM<> ? zxcvbnm, . /"};//a1234567890Qwerchar tp[] = "(_@4620!08!6_0*0442!@186%%0@3=66!!974*3234=&0^3&1@=&0908!6_0*&";//0000000140003478char kp[] = "55565653255552225565565555243466334653663544426565555525555222";//0000000140003438
而outputString则是我们目前需要求取的数据,它只起到了索引的作用,逆算法不难写出:
int main()
{char fp[] = {"1234567890-=!@#$%^&*()_+qwertyuiop[]QWERTYUIOP{}asdfghjkl;'ASDFGHJKL:\"ZXCVBNM<> ? zxcvbnm, . /"};char tp[] = "(_@4620!08!6_0*0442!@186%%0@3=66!!974*3234=&0^3&1@=&0908!6_0*&";//0000000140003478char kp[] = "55565653255552225565565555243466334653663544426565555525555222";//0000000140003438char output[64];for (int i = 0; i < 63; i++){output[i]=find(tp[i],kp[i],fp);}cout << output<<endl;
}
char find(char p1,char p2,char *p3)
{int index = 0;for (int i = 0; i < 95; i++){if (p3[i] == p1){index = i;break;}}while (p3[index/23]!=p2){index += 23;}return index;
}
//private: char * __thiscall R0Pxx::My_Aut0_PWN(unsigned char *)t结果是一个函数声明的字符串,试着将它md5后提交,发现错误,那么就需要继续往上读
那么跟踪outputString是从哪里获得的,能够来到第38行UnDecorateSymbolName函数
UnDecorateSymbolName:https://docs.microsoft.com/en-us/windows/win32/api/dbghelp/nf-dbghelp-undecoratesymbolname
只靠阅读官方文档似乎不太足够,但第38行的大致意思是:完全取消对C++符号的修饰,也就是说,某个C++函数符号被取消修饰后,得到了
“private: char * __thiscall R0Pxx::My_Aut0_PWN(unsigned char *)t”
这样一个函数声明符号
查阅一些文档之后才知道,C++中的符号在编译之后都会被修饰为另外一种样子
https://www.cnblogs.com/yxysuanfa/p/6984895.html
https://blog.csdn.net/Scl_Diligent/article/details/83990429
int Max(int a, int b); //?Max@@YAHHH@Z
double Max(int a, int b); //?Max@@YANHH@Z
double Max1(int a, int b); //?Max1@@YANHH@Z
double Max1(int a, double b); //?Max1@@YANHN@Z我们通过上述代码定义的函数,在编译后都会形成如注释所示的那样的名称

实际操作也验证了我们的想法,那么我们的工作就应该是找到这个经过修饰的名称字符串
根据上面给出的两位大佬总结的编译器名称修饰规则,以及我们已经得出的未修饰名称,可以写出确定的字符串:
?My_Aut0_PWN@R0Pxx@@AAEPADPAE@Zmd5后提交发现还是不对,那就只能再往上读
第28行的函数有些复杂,可以暂时不看;第30~37中涉及了v5,这个v5应是我们输入的内容或是中间内容,也正是v5经过UnDecorateSymbolName变换得到了outputString
函数sub_1400015C0实际上是一个二叉树下序遍历
(我不确定是不是叫下序,总之就是自下往上的遍历方式)
如果不是因为最近正好遇到过类似的题目,可能我也没办法马上认出来,不过两层的递归查找其实也还算明显的;以及,就算不确定是否真是如此,也可以通过动态调试来确定是否为二叉树;并且,如果将其当作二叉树,sub_140001280函数便能够比较自然的想象为二叉树的生成
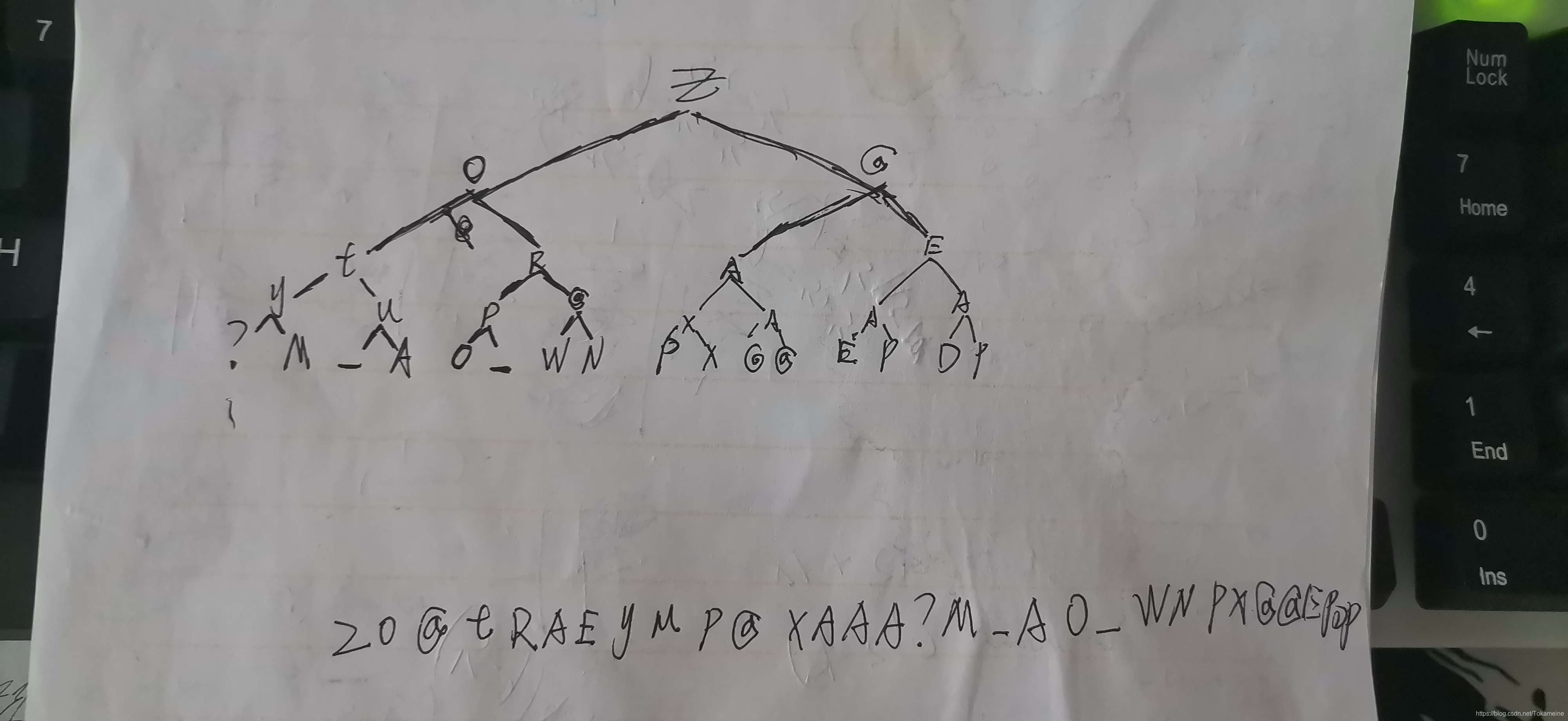
上图是我根据下序遍历的规则手绘出的二叉树,然后再用上序遍历把字符串拼出来得到了flag
(可恶,好久没写过字了,本就难看的字写的更加难看了......)
直接把这个flag输入进去,程序提示正确,我们的猜想也就被验证了

当然,实际操作中我们根本需要这样繁琐的去验证是否为二叉树
大可以通过动调将输入值改为
ABCDEFGHIJKLMNOPQ......等比较好确定的有序的值,然后通过修改PC(程序计数器)跳过第23行的 if 判断,这样就能用较短的数据量确定出实际结构了
但实际上,这为大佬也给出了另外一个比较简单的方法来算出置换后的结果:
https://www.freesion.com/article/6515734088/
个人觉得这要比我手绘二叉树来得简单得多,供参考吧
这篇关于[2019红帽杯]childRE 分析与拓展的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







