acwing-y总基础课算法笔记整理

2024-04-13 21:12
文章标签 算法 整理 笔记 acwing 基础课

本文主要是介绍acwing-y总基础课算法笔记整理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

技巧

vector, 变长数组，倍增的思想size()  返回元素个数 capacity() 容量empty()  返回是否为空clear()  清空front()/back()push_back()/pop_back()begin()/end()[]支持比较运算，按字典序pair<int, int>first, 第一个元素second, 第二个元素支持比较运算，以first为第一关键字，以second为第二关键字（字典序）string，字符串size()/length()  返回字符串长度empty()clear()substr(起始下标，(子串长度))  返回子串c_str()  返回字符串所在字符数组的起始地址queue, 队列size()empty()push()  向队尾插入一个元素front()  返回队头元素back()  返回队尾元素pop()  弹出队头元素priority_queue, 优先队列，默认是大根堆size()empty()push()  插入一个元素top()  返回堆顶元素pop()  弹出堆顶元素定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;stack, 栈size()empty()push()  向栈顶插入一个元素top()  返回栈顶元素pop()  弹出栈顶元素deque, 双端队列size()empty()clear()front()/back()push_back()/pop_back()push_front()/pop_front()begin()/end()[]set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列size()empty()clear()begin()/end()++, -- 返回前驱和后继，时间复杂度 O(logn)set/multisetinsert()  插入一个数find()  查找一个数count()  返回某一个数的个数erase()(1) 输入是一个数x，删除所有x   O(k + logn)(2) 输入一个迭代器，删除这个迭代器lower_bound()/upper_bound()lower_bound(x)  返回大于等于x的最小的数的迭代器upper_bound(x)  返回大于x的最小的数的迭代器map/multimapinsert()  插入的数是一个pairerase()  输入的参数是pair或者迭代器find()[]  注意multimap不支持此操作。 时间复杂度是 O(logn)lower_bound()/upper_bound()unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表和上面类似，增删改查的时间复杂度是 O(1)不支持 lower_bound()/upper_bound()， 迭代器的++，--bitset, 圧位bitset<10000> s;~, &, |, ^>>, <<==, !=[]count()  返回有多少个1any()  判断是否至少有一个1none()  判断是否全为0set()  把所有位置成1set(k, v)  将第k位变成vreset()  把所有位变成0flip()  等价于~flip(k) 把第k位取反

  • 排序

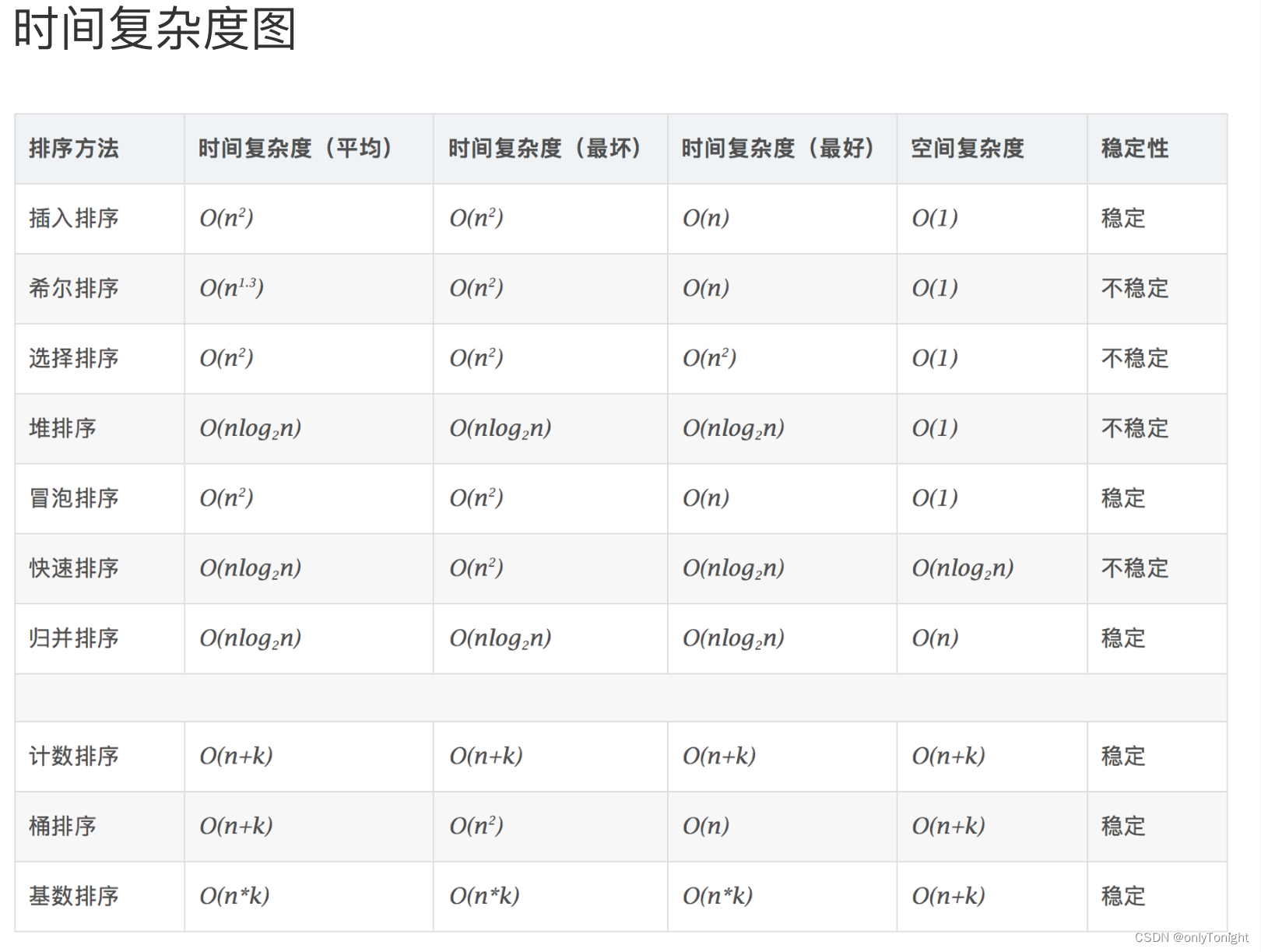
    在这里插入图片描述

  • 基础算法

    • 排序

      • 快速排序

        void quick_sort(int q[], int l, int r)
{if (l >= r) return;
# 取最左、最右、基准点int i = l - 1, j = r + 1, x = q[l + r >> 1];
# 循环，使基准左边都比基准小，右边都比基准大while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}
# 递归排序quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

      • 归并排序

        void merge_sort(int q[], int l, int r)
{if (l >= r) return;# 取中值int mid = l + r >> 1;# 递归排序左右部分merge_sort(q, l, mid);merge_sort(q, mid + 1, r);# 从左右部分中取小值放入新数组int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else tmp[k ++ ] = q[j ++ ];while (i <= mid) tmp[k ++ ] = q[i ++ ];while (j <= r) tmp[k ++ ] = q[j ++ ];# 放回原数组for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

    • 二分

      • 模板

        bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
// 结果是找到序列中满足要求最左边的数
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;    // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用
//结果是找到序列中最右边的数
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}

      • 数的范围

        #include<iostream>
using namespace std;const int N=100010;
int n,m,q[N];
int main(){scanf("%d%d",&n,&m);for(int i=0;i<n;i++) scanf("%d",&q[i]);while(m--){int x; scanf("%d",&x);int l=0,r=n-1,mid;while(l<r){mid = l+r>>1;if(q[mid]>=x) r=mid;else l = mid+1;}if(q[l]!=x) cout<<"-1 -1"<<endl;else{cout<<l<<' ';l=0,r=n-1;while(l<r){mid = l+r+1>>1;if(q[mid]<=x) l=mid;else r=mid-1;}cout<<l<<endl;}}return 0;
}

      • 数的三次方根

        #include<iostream>
using namespace std;
int main(){double x,mid;cin>>x;double l=-10000,r=10000; while(r-l>1e-8){mid=(l+r)/2;if(mid*mid*mid>=x) r=mid;else l=mid;}printf("%lf",l);return 0;
}

    • 高精度

      • 高精度加法

        #include<iostream>
#include<vector>using namespace std;
const int N=1e6+10;vector<int> add(vector<int> &A,vector<int> &B){int t=0;vector<int> C;for(int i=0;i<A.size()||i<B.size();i++){if(i<A.size()) t+=A[i];if(i<B.size()) t+=B[i];C.push_back(t%10);t/=10;}if(t) C.push_back(1);return C;
}
int main(){string a,b;vector<int> A,B;cin>>a>>b;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');vector<int> C = add(A,B);for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);return 0;
}

      • 高精度减法

        #include<iostream>
#include<vector>using namespace std;bool cmp(vector<int> &A,vector<int> &B){if(A.size()!=B.size()) return A.size()>B.size();else{for(int i=A.size()-1;i>=0;i--)if(A[i]!=B[i]) return A[i]>B[i];}return true;
}vector<int> sub(vector<int> &A,vector<int> &B){int t=0;vector<int> C;for(int i=0;i<A.size();i++){t=A[i]-t;if(i<B.size()) t-=B[i];C.push_back((t+10)%10);if(t<0) t=1;else t=0;}while(C.size()>1&&C.back()==0) C.pop_back();return C;
}
int main(){string a,b;vector<int> A,B;cin>>a>>b;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');if(cmp(A,B)){vector<int> C = sub(A,B);for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);}else{printf("-");vector<int> C = sub(B,A);for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);}return 0;
}

      • 乘法

        #include<iostream>
#include<vector>using namespace std;
const int N=1e6+10;vector<int> mul(vector<int> &A,int b){int t=0;vector<int>C;for(int i=0;i<A.size()||t;i++){if(A.size()) t+=A[i]*b;C.push_back(t%10);t/=10;}while(C.size()>1&&C.back()==0) C.pop_back();return C;
}
int main(){string a;int b;vector<int> A;cin>>a>>b;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');vector<int> C = mul(A,b);for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);return 0;
}

      • 除法

        #include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=1e6+10;vector<int> exc(vector<int> &A,int b,int &r){vector<int> C;for(int i=A.size()-1;i>=0;i--){r=r*10+A[i];C.push_back(r/b);r%=b;}reverse(C.begin(),C.end());while(C.size()>1&&C.back()==0) C.pop_back();return C;
}
int main(){string a;int b,r=0;vector<int> A;cin>>a>>b;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');vector<int> C = exc(A,b,r);for(int i=C.size()-1;i>=0;i--) printf("%d",C[i]);cout<<endl<<r<<endl;return 0;
}

    • 前缀和与差分

      一维前缀和

      	for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];while(m--){scanf("%d%d",&l,&r);printf("%d\n",s[r]-s[l-1]);}

      二维前缀和

      for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);

      一维差分

      #include<iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];void insert(int l,int r,int c){b[l]+=c;b[r+1]-=c;
}
int main(){int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) insert(i,i,a[i]);while(m--){int l,r,c; scanf("%d%d%d",&l,&r,&c);insert(l,r,c);	}for(int i=1;i<=n;i++) b[i]+=b[i-1];for(int i=1;i<=n;i++) printf("%d ",b[i]);return 0;
}

      二维差分

      #include<iostream>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c){b[x1][y1]+=c;b[x1][y2+1]-=c;b[x2+1][y1]-=c;b[x2+1][y2+1]+=c;
}int main(){int n,m,q;scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)insert(i,j,i,j,a[i][j]);while(q--){int x1,y1,x2,y2,c;scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);insert(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)printf("%d ",b[i][j]);puts(""); 	}return 0;
}

    • 双指针算法

      最长连续不重复子序列

      #include<iostream>
using namespace std;
const int N=100010;
int a[N],s[N];//用于存储当前在看的区间 
int main(){int n,res=0; cin>>n;for(int i=0;i<n;i++) cin>>a[i];for(int i=0,j=0;i<n;i++){s[a[i]]++;
//		意义：停下来时j~i为连续序列，保证i扫过的数都只出现过一次while(s[a[i]]>1){//正在看的数出现过多次s[a[j]]--;//已经看过的数指针j往后移，使记录数组减小 j++;}res=max(res,i-j+1);} cout<<res; return 0;
}

      数组元素的目标和

      #include<iostream>
using namespace std;
const int N=100000;
int a[N],b[N];
int main(){int n,m,x;cin>>n>>m>>x;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<m;i++) cin>>b[i];for(int i=0,j=m-1;i<n;i++){while(a[i]+b[j]>x) j--;if(a[i]+b[j]==x) cout<<i<<" "<<j;}return 0;
}

    • 位运算-二进制表示中1的个数

      #include<iostream>
using namespace std;
int lowbit(int x){return x&-x;//返回最后一个1的位置 
}
int main(){int n;cin>>n;while(n--){int x;cin>>x;int res=0;while(lowbit(x)) {res++;x-=lowbit(x);}cout<<res<<" ";}return 0;
}

待更新…完整版

这篇关于acwing-y总基础课算法笔记整理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

原文地址:
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.chinasem.cn/article/901225。

相关文章

SpringBoot实现MD5加盐算法的示例代码

SpringBoot实现MD5加盐算法的示例代码

《SpringBoot实现MD5加盐算法的示例代码》加盐算法是一种用于增强密码安全性的技术,本文主要介绍了SpringBoot实现MD5加盐算法的示例代码,文中通过示例代码介绍的非常详细,对大家的学习... 目录一、什么是加盐算法二、如何实现加盐算法2.1 加盐算法代码实现2.2 注册页面中进行密码加盐2.
阅读更多...
Java时间轮调度算法的代码实现

Java时间轮调度算法的代码实现

《Java时间轮调度算法的代码实现》时间轮是一种高效的定时调度算法,主要用于管理延时任务或周期性任务,它通过一个环形数组（时间轮）和指针来实现,将大量定时任务分摊到固定的时间槽中,极大地降低了时间复杂... 目录1、简述2、时间轮的原理3. 时间轮的实现步骤3.1 定义时间槽3.2 定义时间轮3.3 使用时
阅读更多...
Mysql中深分页的五种常用方法整理

Mysql中深分页的五种常用方法整理

《Mysql中深分页的五种常用方法整理》在数据量非常大的情况下,深分页查询则变得很常见,这篇文章为大家整理了5个常用的方法,文中的示例代码讲解详细,大家可以根据自己的需求进行选择... 目录方案一：延迟关联 (Deferred Join)方案二：有序唯一键分页 (Cursor-based Paginatio
阅读更多...
如何通过Golang的container/list实现LRU缓存算法

如何通过Golang的container/list实现LRU缓存算法

《如何通过Golang的container/list实现LRU缓存算法》文章介绍了Go语言中container/list包实现的双向链表,并探讨了如何使用链表实现LRU缓存,LRU缓存通过维护一个双向... 目录力扣：146. LRU 缓存主要结构 List 和 Element常用方法1. 初始化链表2.
阅读更多...
Mysql中InnoDB与MyISAM索引差异详解(最新整理)

Mysql中InnoDB与MyISAM索引差异详解(最新整理)

《Mysql中InnoDB与MyISAM索引差异详解(最新整理)》InnoDB和MyISAM在索引实现和特性上有差异,包括聚集索引、非聚集索引、事务支持、并发控制、覆盖索引、主键约束、外键支持和物理存... 目录1. 索引类型与数据存储方式InnoDBMyISAM2. 事务与并发控制InnoDBMyISAM
阅读更多...
StarRocks索引详解(最新整理)

StarRocks索引详解(最新整理)

《StarRocks索引详解(最新整理)》StarRocks支持多种索引类型,包括主键索引、前缀索引、Bitmap索引和Bloomfilter索引,这些索引类型适用于不同场景,如唯一性约束、减少索引空... 目录1. 主键索引（Primary Key Index）2. 前缀索引（Prefix Index /
阅读更多...
golang字符串匹配算法解读

golang字符串匹配算法解读

《golang字符串匹配算法解读》文章介绍了字符串匹配算法的原理,特别是Knuth-Morris-Pratt（KMP）算法,该算法通过构建模式串的前缀表来减少匹配时的不必要的字符比较,从而提高效率,在... 目录简介KMP实现代码总结简介字符串匹配算法主要用于在一个较长的文本串中查找一个较短的字符串（称为
阅读更多...
通俗易懂的Java常见限流算法具体实现

通俗易懂的Java常见限流算法具体实现

《通俗易懂的Java常见限流算法具体实现》：本文主要介绍Java常见限流算法具体实现的相关资料,包括漏桶算法、令牌桶算法、Nginx限流和Redis+Lua限流的实现原理和具体步骤,并比较了它们的... 目录一、漏桶算法1.漏桶算法的思想和原理2.具体实现二、令牌桶算法1.令牌桶算法流程:2.具体实现2.1
阅读更多...
Python中的随机森林算法与实战

Python中的随机森林算法与实战

《Python中的随机森林算法与实战》本文详细介绍了随机森林算法,包括其原理、实现步骤、分类和回归案例,并讨论了其优点和缺点,通过面向对象编程实现了一个简单的随机森林模型,并应用于鸢尾花分类和波士顿房... 目录1、随机森林算法概述2、随机森林的原理3、实现步骤4、分类案例：使用随机森林预测鸢尾花品种4.1
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2